Дискретно-полевые модели электрических машин. Часть I II

Процесс самовозбуждения генератора моделируется при совместном решении уравнений математической модели МПТРО и урав-

нения (11.5).

Для начала переходного процесса необходимо задать начальные условия: величину остаточной ЭДС, которая может быть определена по характеристике размагничивания материала ярма статора, и начальное, равное нулю, значение тока возбуждения.

Реализация переходного процесса при разомкнутой обмотке якоря производится в следующей последовательности. На каждом временном интервале производится решение уравнения магнитного поля МПТРО, рассчитываются значения векторного потенциала, потокосцепление обмотки возбуждения и динамическая индуктивность Lд .

Из уравнения (11.5) определяется приращение тока возбуждения:

Процесс самовозбуждения будет закончен при равенстве нулю числителя выражения (11.6), а процесс решения повторяется до достижения указанного конечного времени.

Если рассчитывается процесс самовозбуждения при замкнутой на нагрузку якорной цепи генератора, то математическую модель необходимо усложнить. Уравнение магнитного поля МПТРО описывается в этом случае дифференциальным уравнением параболического типа, учитывающим переходный процесс в цепи якоря. Начальные условия при этом должны быть дополнены начальными значениями векторного потенциала во всей исследуемой области и начальным (нулевым) значением тока якоря. В остальной части процедура решения переходного процесса сохраняется. Ниже приведена программа расчёта переходного процесса самовозбуждения МПТРО, а результаты решения – на рис. 11.8.

391

rs1=(hs+del)/(2.*r0); rs2=1+rs1; ra1=(ha+del)/(2.*r0); ra2=1.-ra1; while t<tk

for j=1:n

rs=rs2/(prs(j)*hs*del); ra=ra2/(pra(j)*ha*del); q(j)=r0*r0*(rs+ra)*dx*dx; end

a(1:n)=0.; b(1:n)=0.; c(1:n)=0.; for j=2:n-1

a(j)=0.5*(kz(j)+kz(j-1)); b(j)=0.5*(kz(j)+kz(j+1)); c(j)=a(j)+b(j)+q(j); end

a(1)=0.5*(kz(1)+kz(n)); a(n)=0.5*(kz(n-1)+kz(n)); b(1)=0.5*(kz(1)+kz(2)); b(n)=0.5*(kz(n)+kz(1)); c(1)=a(1)+b(1)+q(1); c(n)=a(n)+b(n)+q(n); rna=pr0*toka*wai*r0*dx/del; rnb=pr0*(tok0+tokb)*wbi*r0*dx/del; rnk=pr0*tokk*wk*r0*dx/del; rnd=pr0*tokd*wd*r0*dx/del;

f1(1:n)=0.; f2(1:n)=0.; f3(1:n)=0.; f4(1:n)=0.; f1(2:4)=rnb; f1(21:23)=rnb; f1(26:28)=rnb; f1(45:47)=rnb; f1(9:11)=-rnb; f1(14:16)=-rnb; f1(33:35)=-rnb; f1(38:40)=-rnb;

f2(1:12)=-rna; f2(13:24)=rna; f2(25:36)=-rna; f2(37:48)=rna; f3(3:10)=rnk; f3(15:22)=-rnk; f3(27:34)=rnk; f3(39:46)=-rnk; f4(1:2)=rnd; f4(11:12)=rnd; f4(13:14)=-rnd; f4(23:24)=-rnd; f4(25:26)=rnd; f4(35:36)=rnd; f4(37:38)=-rnd; f4(47:48)=-rnd;

f(1:n)=f1(1:n)+f2(1:n)+f3(1:n)+f4(1:n);

alf(1)=0.; bet(1)=0.; gam(1)=1.; u(1:n)=0.; v(1:n)=0.; y(1:n)=0.; for j=1:n

rr=c(j)-alf(j)*a(j); alf(j+1)=b(j)/rr; bet(j+1)=(bet(j)*a(j)+f(j))/rr; gam(j+1)=a(j)*gam(j)/rr;

end

u(n-1)=bet(n); v(n-1)=alf(n)+gam(n); for j=n-2:-1:1

u(j)=alf(j+1)*u(j+1)+bet(j+1); v(j)=alf(j+1)*v(j+1)+gam(j+1); end

r1=bet(n+1)+alf(n+1)*u(1); r2=1.-gam(n+1)-alf(n+1)*v(1); y(n)=r1/r2; for j=1:n-1

y(j)=u(j)+y(n)*v(j); end

pot=0.; for j=2:4

pot=pot+d1*(y(j)+y(j+24)-y(j+12)-y(j+36)); end

for j=9:11 pot=pot+d1*(-y(j)+y(j+12)-y(j+24)+y(j+36));

393

end lbm=(pot-pot0)/dib;

br(1)=(y(2)-y(n))/(2.*r0*dx); br(n)=(y(1)-y(n-1))/(2.*r0*dx); for j=2:n-1

br(j)=(y(j+1)-y(j-1))/(2.*r0*dx); end

for j=1:n

bs(j)=y(j)/hs; ba(j)=-y(j)/ha; bbz(j)=tz*br(j)/bz; end

BB=[abs(bs(1:n))]; mub=interp1(X,Y,BB); prs(1:n)=mub(1:n); BA=[abs(ba(1:n))]; mua=interp1(X,Y,BA); pra(1:n)=mua(1:n); BZ=[abs(bbz(1:n))];

for j=1:n

if BZ(j)>2. BZ(j)=2.; end end muz=interp1(X,Y,BZ); for j=1:n

kz(j)=1.+tz*hz/(bz*del*muz(j)); end

v0=pi*n0*r0/30; e(1:n)=-v0*br(1:n); eds=0.; for j=1:12

eds=eds+dli*wai*(e(j)-e(j+12)+e(j+24)-e(j+36)); end

dib=(eds-tokb*rb)*dt/(lbm+lsb); tokb=tokb+dib; pot0=pot; t=t+dt; nn=nn+1; n1(nn)=t; n2(nn)=1000*tokb; n3(nn)=eds; n4(nn)=tokb*rb;

disp(t); disp(tokb); disp(eds); end

plot(n1,n2,n1,n3,n1,n4)

11.2.2. Переходный процесс при включении нагрузки в якорную цепь генератора постоянного тока

Магнитное поле МПТРО описывается нелинейным дифференциальным уравнением (11.1). Поскольку магнитопровод машины шихтованный, будем пренебрегать потерями в стали. В этом случае изменение потокосцепления обмотки добавочных полюсов совпадает во времени с изменениями потокосцепления якоря, т.е. запаздывания потокосцепления добавочных полюсов нет. Это допущение не явля-

394

ется обязательным. Если его не принимать в расчёт, возрастает лишь сложность математического описания электромагнитных процессов.

При протекании токов по обмоткам машины в ней возникает единое магнитное поле, при изменении которого в обмотках наводятся соответствующие ЭДС. В этом случае уравнение Кирхгофа для якорной цепи генератора записывается в виде

+(Rа + Rк+Rд + Rн)iа.

При полной компенсации генератора сумма потокосцеплений обмотки якоря, компенсационной и добавочных полюсов для любого момента времени равна нулю и будут иметь место лишь потокосцепления рассеяния этих обмоток. Поэтому в уравнении (11.8) первые три члена будут отсутствовать. При последовательном соединении обмоток якорной цепи их потокосцепления рассеяния суммируются. Поскольку потоки рассеяния замыкаются вокруг проводников по воздуху, то потокосцепления пропорциональны соответствующим токам, причём коэффициенты пропорциональности – индуктивности рассеяния La , Lк , Lд являются постоянными

величинами. Уравнение (11.8) для МПТРО упрощается и записывается следующим образом:

Уравнение цепи возбуждения

Потокосцепление обмотки возбуждения зависит не только от тока этой обмотки, но и от других токов машины. Влияние других обмоток в теории электрических машин учитывается введением

395

коэффициентов взаимоиндукции [11]. В нашем случае это влияние учитывается через магнитное поле машины, которое определяется всеми токами генератора.

Для моделирования переходного процесса при включении сопротивления нагрузки в якорную цепь используется приведённая выше программа с изменениями, соответствующими уравнениям якорной цепи (11.9) и цепи возбуждения (11.10).

В качестве начальных условий задаются нулевые значения тока якоря, производных потокосцепления и тока возбуждения, установившееся значение ЭДС обмотки якоря и тока возбуждения.

После момента коммутации из уравнения (11.9) определяется производная тока якоря:

и ток якоря на первом временном интервале:

При полной компенсации потока якоря изменение величины тока якорной цепи не влияет на характер и величину магнитного поля машины, которое остаётся в любой момент времени таким же, как и в режиме холостого хода. Поэтому изменения потокосцепления обмотки возбуждения не происходит, и ток возбуждения при указанных условиях не изменяет своей величины. На втором и последующих временных интервалах производная тока якоря определяется с учётом тока якоря:

В дальнейшем процесс решения повторяется до тех пор, пока не будет достигнуто время окончания переходного процесса.

396

Если исследуется переходный процесс с частичной компенсацией реакции якоря, то на каждом временном интервале необходимо производить уточнение тока возбуждения. В этом случае изменение тока якоря влечёт изменение потокосцеплений всех обмоток, включая обмотку возбуждения. Изменение потокосцепления обмотки возбуждения приводит к возникновению переходного процесса в цепи возбуждения. При заданной величине напряжения возбуждения, постоянных параметрах цепи возбуждения на каждом временном интервале решается уравнение (11.10) таким же образом, как и уравнение якорной цепи.

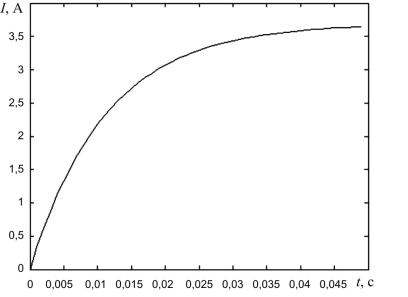
На рис. 11.9 приведена зависимость тока якоря от времени, рассчитанная для МПТРО с полной компенсацией реакции якоря.

Рис. 11.9. Зависимость тока якоря от времени переходного процесса при включении нагрузки в якорную цепь МПТРО

397

11.2.3. Пусковые режимы двигателя постоянного тока

Основное назначение МПТРО – работа в режиме двигателя. Для реализации этого режима к якорю с последовательно включёнными обмотками добавочных полюсов и компенсационной подключают к источнику постоянного тока. По обмотке возбуждения пропускают ток возбуждения, создающий в машине основное магнитное поле. Как и в режиме генератора, компенсационная обмотка и обмотка дополнительных полюсов создают свои поля, которые компенсируют реакцию якоря на всём протяжении полюсного деления двигателя.

Математическая модель двигателя с распределёнными обмотками статора отличается от модели генератора уравнением якорной цепи и введением уравнения движения, описывающего механический переходный процесс.

Для цепи якоря уравнение Кирхгофа в общем виде записывается как

обмоткой возбуждения. Если машина является полностью компенсированной, то сумма трёх первых членов равна нулю и уравнение упрощается:

Это уравнение позволяет при заданном напряжении сети, известной частоте вращения и параметрах якорной цепи рассчитать приращение тока якоря и найти его величину на каждом временном интервале.

Уравнение движения

398

определяет величину ускорения двигателя во время переходного процесса, когда момент двигателя не равен моменту нагрузки M д ≠ M н . В установившемся режиме динамический момент равен

нулю и частота вращения является постоянной величиной.

При моделировании электромеханических переходных процессов МПТРО в математической модели необходимо, помимо изменения тока якоря, учитывать изменение частоты вращения и пропорциональную ей противоЭДС якорной обмотки. Необходимо также скорректировать начальные условия в соответствии с реальными условиями решаемой задачи. Реализация математической модели осуществляется с использованием тех же конечно-разностных методов, что и для генераторов постоянного тока.

На рис. 11.10 приведена зависимость тока и электромагнитного момента двигателя от времени электромагнитного переходного процесса при неподвижном якоре. Для двигателя с полной компенсацией момент пропорционален току, что и подтверждено расчётом переходного процесса.

Рис. 11.10. Зависимость тока и момента МПТРО от времени электромагнитного переходного процесса

399

На рис. 11.11 показаны зависимости частоты вращения и электромагнитного момента от времени при реостатном пуске двигателя из неподвижного состояния до установившегося режима. При расчёте этого режима электромагнитными процессами двигателя обычно пренебрегают, полагая, что они протекают значительно быстрее механических. Для двигателей большой мощности с большими инерционными массами такое положение является вполне справедливым. Если же анализируются двигатели постоянного тока малой мощности при незначительных моментах

Рис. 11.11. Зависимость момента и частоты вращения от времени при реостатном пуске двигателя постоянного тока

инерции, то наряду с механическими переходными процессами желательно учитывать и электромагнитные. Точность расчёта при этом повышается и картина переходного процесса становится ближе к реальному.

400