Дискретно-полевые модели электрических машин. Часть I II

Потокосцепления каждой из обмоток рассчитываются через значения векторных потенциалов в точках, соответствующих координатам расположения проводников рассматриваемой обмотки (8.52)–(8.55). Величины магнитной индукции в зазоре двигателя, плотности тока ротора, электромагнитного усилия и момента двигателя рассчитываются через найденные значения векторного потенциала по известным соотношениям.

Совместное решение уравнения магнитного поля, системы уравнений Кирхгофа, и уравнений потокосцеплений обмоток производится описанным ранее методом суперпозиции.

Результаты математического моделирования многоскоростного однофазного электродвигателя фирмы SANYO (Япония), включаемого по изображённым на рис. 10.10 схемам, с ёмкостью конденсатора 4 мкФ представлены в табл. 10.3.

Таблица 1 0 . 3

Результаты математического моделирования многоскоростного однофазного электродвигателя

341

Сравнение результатов моделирования с экспериментальными данными показывает их хорошее качественное и количественное совпадение. Так, величина погрешности тока при включении обмоток по рис. 10.10, в не превышала 8 %, напряжения на конденсаторе – 3,5 %, потребляемой мощности– 6,7 %, момента– 18 %. Наибольшие расхождения, наблюдаемые в величинах моментов, объясняются тем, что в результатах моделирования представлены значения электромагнитных моментов, а измеренные значения – это моменты на валу двигателя.

На рис. 10.12 представлены зависимости электромагнитных моментов электродвигателя от скольжения для схем включения обмоток, изображённых на рис. 10.10, полученные в результате математического моделирования. Особенностью этих характеристик является различная величина критического момента и, следовательно, их различная жесткость в рабочей области скольжений. Это обстоятельство обеспечивает достаточный диапазон регулирования частоты вращения при вентиляторном моменте нагрузки.

Рис. 10.12. Зависимости электромагнитного момента многоскоростного конденсаторного двигателя от скольжения для различных схем соединения обмоток статора (1 – рис. 10.10, в; 2 – рис. 10.10, б; 3 – рис. 10.10, а)

342

На рис. 10.13 приведены векторные диаграммы токов при скольжении s = 0,1 для различных схем включения обмоток. На этих диаграммах видно, что между токами рабочей и конденсаторной обмоток существуют временные сдвиги фаз, обеспечивающие возникновение вращающегося магнитного поля.

В процессе регулирования частоты вращения в многоскоростных конденсаторных электродвигателях возникают переходные процессы, связанные с изменением схем включения обмоток статора.

Рис. 10.13. Векторные диаграммы токов многоскоростного двигателя при различных схемах включенияобмоток: а– рис. 10.10, а;

б – рис. 10.10, б; в – рис. 10.10, в

в

343

Эти процессы протекают, как правило, при незатухших магнитных полях и могут вызвать значительные броски токов и перенапряжения в обмотках двигателя и фазосмещающем конденсаторе.

Магнитное поле в зазоре конденсаторного двигателя описано уравнением в частных производных параболического типа (8.12):

которое дополняется краевыми и начальными условиями. Плотность сторонних токов, как и при решении стационарных задач, определяется путём решения уравнений Кирхгофа для статорных обмоток двигателя.

Для схемы на рис. 10.10, а:

344

Потокосцепления каждой из обмоток рассчитываются суммированием потоков витков этой обмотки, а поток витка определяется через значения векторного потенциала в точках исследуемой области с координатами расположения проводника данного витка (8.52)–(8.55).

Используя граничные условия периодического типа и начальные условия, соответствующие решаемой задаче, можно решить систему уравнений магнитного поля, Кирхгофа и потокосцеплений фаз двигателя относительно векторного потенциала. Величины магнитной индукции, плотноститокавторичнойсредыдвигателяиэлектромагнитногомомента определяютсяпоизвестнымсоотношениям(7.15), (8.11), (8.98).

Использование описанной методики позволило рассчитать электромагнитные и электромеханические переходные процессы для различных схем соединений обмоток двигателя и выявить особенности их протекания. Установившиеся значения исследуемых величин соответствуют их значениям, полученным при решении стационарных задач, близким к экспериментальным данным. Некоторые из полученных результатов представлены ниже.

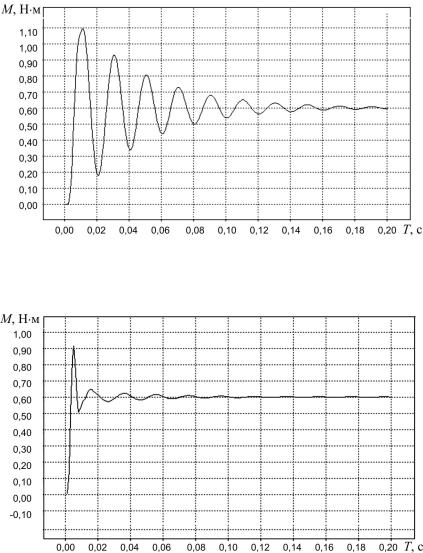
На рис. 10.14 показана зависимость электромагнитного момента неподвижного двигателя от времени электромагнитного процесса при включении его обмоток по схеме на рис. 10.10, в с максимальной частотой вращения. На рис. 10.15 представлена та же зависимость для двигателя с вращающимся ротором (скольжение s = 0,05).

Сравнение этих зависимостей показывает, что переходные процессы в этих случаях отличаются знаками и временем затухания переходных составляющих электромагнитного усилия. На начальной стадии процесса переходная составляющая электромагнитного момента

345

определяется взаимодействием экспоненциальных и периодических компонент магнитной индукции и токов ротора. Поэтому величина момента изменяется во времени по закону, близкому к синусоидальному. Установившиеся значения моментов имеют различные величины, а кривая момента при вращающемся роторе имеет периодическую составляющую, изменяющуюся с двойной частотой сети. Наличие периодической составляющеймоментаможнообъяснитьследующимипричинами.

Магнитное поле конденсаторного двигателя при заданной величине фазосмещающей ёмкости имеет вращающуюся и пульсирующую составляющие. Пульсирующую составляющую можно представить в виде суммы вращающихся в противоположных направлениях полей с одинаковыми амплитудами. Каждое из этих полей наводит в обмотке ротора соответствующие ЭДС, под действием которых протекают токи. Взаимодействие прямых и обратных составляющих магнитного поля с одноимёнными составляющими токов ротора обусловливает появление электромагнитных моментов различных направлений, установившиеся величины которых содержит лишь неизменные во времени составляющие моментов.

Рис. 10.16. Зависимость электромагнитного момента от времени переходного процесса МКЭД при неподвижном роторе

при благоприятной фазе коммутации

347

Взаимодействие разноимённых составляющих магнитных полей и токов ротора приводит к возникновению электромагнитных моментов, установившиеся значения которых содержат периодические составляющие, изменяющиеся во времени с двойной частотой сети. При неподвижном роторе величины прямых и обратных периодических составляющих равны по величине и компенсируют друг друга. С увеличением частоты вращения амплитуды пульсирующих составляющих становятся различными, что и приводит к появлению этой составляющей в кривой электромагнитного момента. Анализ результатов расчётов показывает, что амплитуда периодической составляющей двойной частоты возрастает с увеличением скорости вращения ротора.

Другой особенностью протекания переходного процесса МКЭД является нарушение инвариантности начальной фазы коммутации. Проведённые исследования показывают, что при благоприятной фазе коммутации максимальная величина электромагнитного момента и время затухания его переходных составляющих снижается. Сравнение зависимостей электромагнитного момента от времени переходного процесса для МКЭД с неподвижным ротором, представленных на рис. 10.17 (неблагоприятная фаза) и рис. 10.15 (благоприятная фаза), подтверждает этот вывод.

При моделировании электромеханических переходных процессов было принято, что момент нагрузки имеет вентиляторный характер и описывается следующим выражением:

Система уравнений дополнялась уравнением движения, и частота вращения ротора оказывается в этом случае переменной величиной. Характер протекания переходного процесса при переменной частоте вращения при включении обмоток статора по схеме на рис. 10.10, б показан на рис. 10.17.

На начальной стадии при низкой частоте вращения электромеханический переходный процесс весьма близок к процессу при неподвижном роторе (см. рис. 10.14). По мере увеличения частоты вращения возрастает периодическая составляющая момента с двойной частотой

348

сети, а среднее значение момента, достигнув максимума, уменьшается. Установившееся значения частоты вращения наблюдается при равенстве среднего значения момента двигателя и момента нагрузки.

Рис. 10.17. Зависимость электромагнитного момента (M)

и частоты вращения (ω) МКЭД от времени переходного процесса

Для других схем включения статорных обмоток двигателя характер протекания электромеханического переходного процесса сохраняется, а величины установившейся частоты вращения соответствуют стационарному режиму.

10.4. УНИВЕРСАЛЬНЫЙ АСИНХРОННЫЙ ДВИГАТЕЛЬ

Помимо трёхфазных и однофазных промышленностью выпускаются универсальные асинхронные двигатели, которые, являясь по конструкции трёхфазными, могут работать от однофазной сети, при наличии фазосмещающего элемента и при включении обмоток статора по специальным схемам.

349

Среди большого разнообразия схем включения обмоток статора [50] наибольшее распространение получили схемы, изображённые на рис. 10.18.

Первая из этих схем используется в том случае, если обмотка статора имеет шесть выводов. При этом схема двигателя соответствует схеме однофазного конденсаторного двигателя: две последовательно соединённые фазы образуют рабочую обмотку, а третья фаза с включённым конденсатором – конденсаторную (см. рис. 10.18, а).

Две другие схемы (см. рис. 10.18, б, в) используются в том случае, если обмотки статора соединены в «звезду» без доступа к нейтральной точке или треугольник.

Проектирование универсальных асинхронных двигателей связано с расчётом их параметров и рабочих характеристик, что представляет собой весьма сложную задачу. Сложность аналитического расчёта универсальных асинхронных двигателей заключается в том, что система питающего напряжения является однофазной, а сам двигатель включён по несимметричным схемам. Поэтому на практике, чаще всего, величину ёмкости фазосмещающих конденсаторов подбирают опытным путём, руководствуясь определёнными критериями [45].

Рис. 10.18. Схемы включения обмоток трёхфазных асинхронных двигателей по однофазным схемам

350