Теплофизические явления в полимерных материалах при интенсивном и кр

ме того, из различных вышеназванных видов таких нагрузок наименее изучено влияние СВЧ-излучения. Действие СВЧ-излучения рассматривается лишь в связи с выходом из строя технических конструкций за счет нарушения работы радиоэлектронной аппаратуры управления и обеспечения жизнедеятельности. Также только начинается изучение действия СВЧ-излучения на человека. По вопросу поведения высокоэнергетических материалов при таком виде воздействия практически нетдаже отрывочных сведений.

По изложенным причинам автора заинтересовали три вопроса:

1.Возможно ли построить модель для расчета параметров детонационного процесса в сложных смесевых взрывчатых составах

ираспространить эту модель на другие теплофизические параметры как взрывчатых составов, так и смесевых полимерных составов?

2.Возможно ли проследить изменение различных свойств твердых и жидких материалов (веществ) при изменении времени действия нагрузки либо при изменении скорости деформирования (которая является величиной, обратной времени нагрузки)

иполучить практические следствия для описания различий в детонационных свойствах высокоэнергетических материалов: взрывчатых и полимерных составов?

3.Возможно ли описать механические эффекты, и в частности волновые процессы, в деталях из полимерных материалов при их облучении импульсным СВЧ-излучением?

Имеющаяся по этим вопросам информация приведена далее.

1.2. Модели и способы расчета параметров смесевых материалов

Одним из способов описания физических свойств композитов является приближение эффективных характеристик. Оно имеет место тогда, когда характерный размер изменения различных полей в композите много больше характерных размеров структурных элементов композита. При этом композит в целом можно рассматривать как статистически однородную среду, поведение которой опи-

11

сывается именно эффективными характеристиками. Очевидно, указанное приближение можно назвать длинноволновым.

Ниже дан краткий аналитический обзор методов расчета значений эффективных характеристик.

Правило смесей

Правило смесей предполагает аддитивность свойств компонентов, составляющих смесь. Один из подходов резюмирован Дж. Х. Ван Флеком [2], который отмечает, что некоторые свойства смесевых материалов подчиняются правилу смесей. Однако способ нахождения необходимых средневзвешенных характеристик зависит от формы и распределения каждой фазовой составляющей. Соответственно этим двум последним факторам изменяется и вид математического выражения для вычисления значения требуемого параметра. На примерах плотности, теплопроводности автор работы [2] демонстрирует справедливость правила смесей.

Свойства материала, определяющиеся градиентом какоголибо параметра, зависят от геометрии структуры. В простейшем случае эта зависимость связана с разными способами передачи энергии. В других случаях поведение каждой фазы зависит от характеристик смежных фаз или зерен.

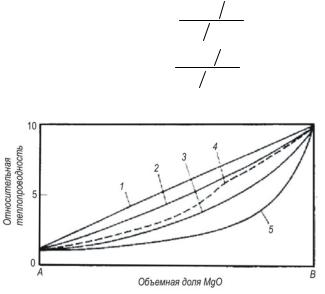
Теплопроводность, а также электропроводность многофазных материалов подчиняются правилу смесей, но способ нахождения средневзвешенных характеристик зависит от формы и распределения каждой фазовой составляющей. Упрощенные типичные модели структуры материалов представлены на рис. 1.1. Хотя эти модели в равной степени применимы при определении теплопроводности и электропроводности материала, все дальнейшие уравнения будут составлены для теплопроводности.

В первой модели (рис. 1.1, а) имеет место параллельная проводимость, поэтому средняя теплопроводность материала kмат

представляет собой сумму составляющих k1, k2,…, пропорциональных объему или площади поперечного сечения отдельных фаз:

12

При рассмотрении переноса электрических зарядов в модели с последовательной проводимостью удобнее использовать электросопротивление: в таком случае уравнение с обратными величинами становится ненужным.

Рис. 1.1. Модели структурымногофазных материалов: а– параллельное распределение фаз; б– последовательноераспределениефаз; в– матрица сдиспергированной фазой

Если структура двухфазная,

В этом случае величина теплопроводности материала с аналогичной структурой оказывается меньше полученной путем линейной интерполяции теплопроводности фаз в соответствии с их относительным объемом (рис. 1.2).

Если одна фаза диспергирована в матрице другой фазы, как это обычно имеет место в структурах, то более сложная интерполяция приводит к соотношению

13

Рис. 1.2. Зависимость теплопроводности от объемной доли второй фазы в системе MgO–Mg2SiO4: 1 – уравнение (1.1); 2 – уравнение (1.4), kм =10kд; 3 – уравнение (1.4), kд =10kм;

4 – уравнение (1.2); 5 – уравнение (1.3)

Здесь индекс «м» относится к матричной фазе, а индекс «д» – к диспергированной фазе.

График уравнения (1.4) представлен на рис. 1.2 для двух экстремальных случаев: при kм kд =10 и при kм 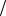kд = 0,1 . Как и мож-

но было предполагать, обе кривые располагаются между соответствующими кривыми параллельной проводимости [уравнение (1.1)] и последовательной проводимости [уравнение (1.3)]. Результаты изучения теплопроводности двухфазных смесей периклаза и форстерита (MgO–Mg2SiО4) показали хорошее согласие с уравнением (1.4) по краям области исследованных составов, когда одна фаза рассматривается как матричная, а другая – как диспергированная. Однако в области промежуточных составов, ко-

14

гда ни одна из фаз не образует непрерывной структуры, теплопроводность материала принимает переходные значения между обеими кривыми на рис. 1.2.

Обобщенная проводимость

Данный подход предложен В.И. Оделевским [3]. Оделевский на формальном совпадении дифференциальных уравнений скалярных и векторных полей для стационарных потоков тепла, электрических зарядов, электрической и магнитной индукций строит метод расчета обобщенной проводимости гетерогенных систем для таких характеристик, как электропроводность, теплопроводность, диэлектрическая и магнитная проницаемость. При некоторых упрощающих допущениях, в частности допущениях об одинаковости по форме и объему частиц, слагающих фазы; о справедливости теоремы пропорциональности в частном случае стационарного потока, а также при использовании известных расчетных методов Лорентца (схема взаимодействия точечных индуцированных полей) и Кувшинского (обращенный метод сеток) автор работы [3] получает конечные выражения для расчета значений упомянутых характеристик, пригодность которых проверяет для плоской задачи, т.е. для тонких пленок равномерной толщины.

Гетерогенные системы на практике имеют не меньшее, если не большее, значение, чем системы гомогенные. К ним относятся такие технические материалы, как фарфор и разного рода электро- и теплоизоляционная керамика, асбест, пластические массы (с наполнителями), кабельная и машинная изоляция, бумажные конденсаторы, огромное большинство металлических сплавов. Почва, вода со взвешенными в ней коллоидными частицами, пыльный воздух также представляют собой примеры гетерогенных систем.

Функцию, выражающую удельное свойство а гетерогенной системы через удельные характеристики аi фаз, назовем метрической функцией гетерогенной системы.

Примеры метрических функций: 1) плотность системы

15

d = ∑diϑi ,

(i)

где ϑi – объемная концентрация; di – плотность i-й фазы; 2) удельный объем

v = ∑1ϑi ,

(i) vi

где vi – объем i-й фазы;

3) диэлектрическая проницаемость слоистого диэлектрика а) если поле направлено вдоль слоев,

ε = ∑εi ϑi ,

(i)

б) если поле направлено перпендикулярно слоям,

ε = ∑1ϑi ,

(i) εi

где εi – диэлектрическая проницаемость i-й фазы;

4) диэлектрическая проницаемость среды с удаленными друг от друга сферическими включениями (Вагнер)

ε = ε0 1+ 3ϑ1 εε11++2εε00 ,

где индекс «0» относится к среде, «1» – к включениям.

Ни в одну из приведенных формул не входят абсолютные размеры частиц; в них фигурируют только объемные концентрации фаз. Это обстоятельство отнюдь не случайно и может быть обобщено на все случаи, в которых отсутствуют или исключены из рассмотрения поверхностные, линейные или точечные эффекты (например, в случае электропроводности, если можно пренеб-

16

речь контактными эффектами). Для случаев чисто объемных эффектов можно написать в общем виде:

a = F (ai(n), ϑi(n) ),

где символ ai(n) обозначает совокупность n аргументов; ai харак-

теризует удельное свойство i-й фазы. При этом подразумевается, что в пределах любой фазы ai = const.

Следует учитывать, что в общем случае аргументами метрической функции F могут служить также отношения линейных параметров, характеризующих геометрию системы, однако можно формально включить их в общий символ F.

Далее дан расчет группы свойств, объединенных под названием «обобщенная проводимость» (электропроводность, теплопроводность, диэлектрическая и магнитная проницаемость). Это объединение основывается на известном формальном совпадении дифференциальных уравнений скалярных и векторных полей для стационарных потоков тепла, электрического тока, электрической и магнитной индукции, поэтому в дальнейшем мы будем пользоваться методами любой из этих областей для решения конкретных задач, не придавая значения тому, какая величина представляет в данном варианте расчета обобщенную проводимость Λ: электропроводность σ, диэлектрическая проницаемость ε, маг-

нитная проницаемость µ или теплопроводность λT .

Из соображений элементарной теории размерностей следует, что метрическая функция F гетерогенной системы должна быть однородной функцией первой степени от совокупности аргументов ai(n), т.е.

F (mai(n), ϑi(n) )= mF (ai(n), ϑi(n) ),

где m – локальная константа.

17

Эта простая, но весьма важная теорема пропорциональности в специальном случае стационарного потока может быть также непосредственно выведена из решений соответствующих дифференциальных уравнений.

Обобщенная проводимость системы в отличие, например, от плотности является структурно-чувствительным свойством: достаточно указать на важность последовательного или параллельного соединения слоев, поскольку даже не изменение структуры, а лишь изменение ориентации системы может радикально изменить ее количественную характеристику.

Гетерогенные системы можно подразделить на следующие два основных типа: а) матричные системы, в которых одна фаза образует связную матрицу при любой объемной концентрации этой фазы, большей нуля; б) статистические смеси, в которых частицы распределяются хаотически, не образуя никаких регулярных структур. Далее исследованы простейшие матричные структуры. В этой области известно большое количество работ, однако развиваемые в указанных работах методы не позволяют рассчитывать обобщенную проводимость при предельно высокой концентрации включений, доходящей до 1; кроме того, многообразие формул затрудняет пользование ими.

Предполагается, что частицы, слагающие фазы системы, приблизительно одинаковы по объему и по форме. Здесь и в дальнейшем индекс «0» отнесен к матричной фазе, индекс «1» – к включениям. В зависимости от концентрации включений расчет распадается на две части:

А. Случай малых концентраций. Обратимся к электростатической задаче. Сопоставим систему I со вспомогательной системой II, в которой диэлектрические проницаемости фаз уменьше-

матричной фазы. При использовании расчетного метода Лорентца, включающего схему взаимодействия точечных индуцированных диполей, можно получить следующую формулу:

18

Б. Случай больших концентраций. Рассмотрим токовую задачу. Примем для решения обращенный метод сеток, общая идея которого принадлежит Кувшинскому.

Во всей области концентраций от ϑ = 0 до ϑ =1 обобщенная проводимость матричной системы с кубическими включениями, центры которых образуют кубическую решетку, а грани парал-

Далее автор работы [3] проверяет пригодность полученных выражений для решения плоской задачи. Пусть в матричной системе включения представляют собою длинные параллельные призмы или цилиндры, такова, например, структура некоторых типов изделий из стекловолокна, железобетона с параллельными армирующими стержнями и некоторых видов пустотелого кирпича (в последних двух случаях интерес представляет расчет теплопроводности).

При относительно длинных стержнях можно исключить из рассмотрения третью координату (плоская задача). В итоге для всего диапазона концентраций включений от ϑ = 0 до ϑ =1

Выражение (1.6) совпадает с формулой Максвелла для удельного сопротивления (при замене σ1 =ρ и соответствующем преобразовании):

а также с формулой Винера:

εε+−2εε00 = εε11+−2εε00 ϑ1.

Как нетрудно убедиться, известная формула Релея с численной поправкой Рунге:

также переходит в (1.6), если отбросить несущественный третий член в знаменателе. Аналогично (1.7) совпадает с формулой Винера для цилиндрических включений:

а также практически и с соответствующей формулой Релея: