Прочность и устойчивость статически неопределимых рам учебно-методи

Рис. 2.21

Результаты расчета, выполненные по описанному выше алгоритму, приведены в табл. 2.3. Линии влияния неизвестных и внутренних усилий показаны на рис. 2.22.

61

Рис. 2.22

3. РАСЧЕТ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ РАМ НА УСТОЙЧИВОСТЬ

3.1. Основные положения расчета плоских рам на устойчивость

Рассматриваются рамы со сжатыми и в некоторых случаях со сжатыми и растянутыми элементами при узловой нагрузке.

Если пренебрегать укорочениями сжатых и удлинениями растянутых элементов рам, а также собственным весом ригелей, то такие рамы до потери устойчивости не будут иметь изгиба и, следовательно, для них возможна обычная постановка вопроса об устойчивости.

Продольные силы в элементах рамы до потери устойчивости при узловой нагрузке, как правило, определяются просто.

Такой приближенный расчет рам на устойчивость при узловых нагрузках способен лишь указать на самые большие и обычно недостигаемые значения продольных сил в элементах рамы, при которых происходит потеря устойчивости в упругой стадии. При существующем с самого начала нагружения изгибе элементов рамы весьма быстро растут в деформированном состоянии напряжения от изгибающего момента и краевые напряжения часто достигают предела текучести еще до наступления критического состояния, определяемого по упругой стадии при узловых нагрузках. Поэтому, если речь идет о рамах строительных конструкций, часто приходится говорить о предельной несущей способности рамы, т.е. о критической нагрузке второго рода, а она во многих случаях бывает меньше критической нагрузки в упругой стадии, вычисленной при узловой нагрузке. Все зависит от соотношения между напряжениями от продольных сил и изгибающих моментов.

Не следует забывать о пределах применимости получаемых критических сил в упругой стадии. При исследовании устойчивости рамы принимаются следующие основные допущения:

64

1.Рассматривается только узловая нагрузка, не вызывающая поперечного изгиба стержней.

2.Стержни считаются нерастяжимыми и несжимаемыми.

3.Изменение расстояния между концами стержня, которое получается благодаря его изгибу, не учитывается (это допущение неприменимо при определении работы внешних сил, если задача решается энергетическим методом).

4.Учитываются продольные силы, возникающие до потери

устойчивости. Влияние приращений продольных сил ∆N, возникающих в момент потери устойчивости, не учитывается.

5. При определении поперечных сил в изогнутых стержнях не учитывается изменение угла наклона сечения за счет изгиба стержня.

Пока нагрузка меньше критической, единственная возможная форма равновесия – прямолинейная. Существует такое критическое значение нагрузки (Fкр – критический параметр этой нагрузки), при котором, кроме прямолинейного (являющегося при данной нагрузке неустойчивым) положения равновесия, возможно еще изогнутое равновесное состояние. Поскольку новое изогнутое состояние есть состояние равновесия, расчет может быть произведен любым из методов, применяемых к расчету равновесных систем, в том числе методом сил или методом перемещений.

При выборе основной системы следует всегда стремиться к тому, чтобы в основной системе не возникало изгибающих моментов от заданной нагрузки. Например, для рамы, показанной на рис. 3.1, а, это условие удовлетворяется при основной системе, показанной на рис. 3.1, б. Для основной системы, показанной на рис. 3.1, в, это условие не удовлетворяется, так как от действия нагрузки F3 правая стойка испытывает изгиб.

Итак, в методе сил элементы, испытывающие сжатие от действия узловых нагрузок, в основной системе должны иметь либо шарнирно-неподвижные опоры, либо один защемленный, а другой свободный конец. Метод сил может оказаться целесо-

65

образным при расчете устойчивости рам с большим числом стержней, из которых только немногие имеют продольные силы, отличные от нуля.

Рис. 3.1

Врасчетах на устойчивость для большинства типов рам метод перемещений требует более простых и менее трудоемких вычислений, чем метод сил.

Вканонических уравнениях метода сил и метода переме-

щений отсутствуют грузовые члены ∆iF и RiF, так как переход стержней рамы в искривленное состояние возникает не от действия изгибающей нагрузки.

Системы уравнений приобретают вид:

• для метода сил

δ11x1 +δ12 x2 +... +δ1n xn = 0; δ21x1 +δ22 x2 +... +δ2n xn = 0;

……………………………..

δn1x1 +δn2 x2 +... +δnn xn = 0;

66

• для метода перемещений

r11z1 +r12 z2 +... +r1n zn = 0;

r21z1 +r22 z2 +... +r2n zn = 0;

……………………………

rn1z1 +rn2 z2 +... +rnn zn = 0.

В изогнутом равновесном состоянии xi ≠ 0 и zi ≠ 0, систе-

ма же линейных однородных уравнений дает ненулевое решение для неизвестных только при равенстве нулю определителя, составленного из коэффициентов при неизвестных. Составляем определитель и, приравняв его к нулю, получаем так называемое уравнение устойчивости, из которого и определяем критический параметр нагрузки:

Заметим, что здесь нельзя упускать из виду тривиальное решение. В тех случаях, когда потеря устойчивости физически возможна при z1... zn =0 (или x1... xn =0), т.е. когда возможно

при этих данных совпадение некоторых форм потери устойчивости основной системы и системы заданной, она также должна быть рассмотрена.

В этих уравнениях δik – перемещения и rik – реакция по направлению i от единичных лишних неизвестных при наличии продольных сил в стержнях. Продольная сила Ni является здесь дополнительным, кроме i и EJ, параметром, характеризующим сжатый стержень. Таким образом, для применения метода сил или метода перемещений в задачах устойчивости необходимо знать функциональные зависимости от N коэффициентов податливости и жесткости сжатых стержней.

67

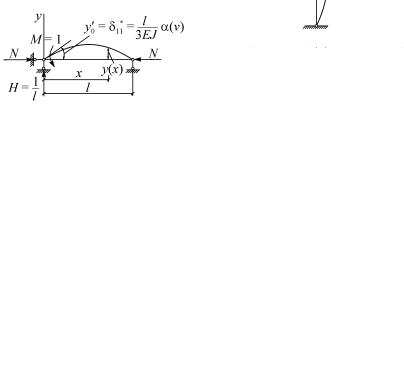
Определение таких зависимостей рассмотрим на примере рамы, показанной на рис. 3.2, а. На рис. 3.2, б, в показаны основные системы метода сил и метода перемещений. Рассмотрим решение задачи методом сил. Сжатая стойка в основной системе представляет собой шарнирно опертый стержень (рис. 3.3). Воспользуемся решением уравнения изгиба сжатого стержня в форме метода начальных параметров:

Рис. 3.2

Рис. 3.3

68

В нашем случае

Податливость основной системы по направлению х1, т.е. угол раскрытия δ11 запишем в виде суммы податливостей стержней:

δ11 = 3EJl α(v) + 3EJl .

Каноническое уравнение δ11x1 =0. Приравнивая δ11 нулю,

получаем

α(v) +1 =0,

тогда

α(v) = −1.

Минимальный корень этого уравнения vmin =3,725, тогда

v2 EJ 10,4EJ

Nкр .

Ктакому же результату мы придем, используя метод пере- мещений: = Fкр = minl2 = l2

69

Жесткость основной системы по направлению перемещения z1

уравнения ϕ1(v) = −1.

Коэффициент жесткости r11* сжатого упругого стержня

имеет такой же вид, как и при расчетах без учета продольнопоперечного изгиба, отличаясь лишь некоторым безразмерным множителем – функцией безразмерного параметра v.

Для вычисления rik* , конечно, не обязательно прибегать

к использованию метода сил, как в рассмотренном примере, их можно получать непосредственно путем использования решения дифференциального уравнения изгиба сжато-изогнутого стержня (например, в форме метода начальных параметров). Так, для

Рис. 3.4

70