
Аналитическая геометрия
..pdf
|
|
|
|
|
|
|
x2 |
|
y2 |
1 , |
(4.3.2) |
|
|
|
|
|
|
|
a2 |
b2 |
|||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
1 |
|
1 |
|
|
|
где a a |
1 h2 |
, b |
b |
1 h2 |
. Уравнение (4.3.2) является уравнением |
||||||
1 |
|
c2 |
1 |
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
эллипса, подобного эллипсу в плоскости xOy , с коэффициентом подобия |
|||||||||||
1 h2 |
и полуосями a и b . Нарисуем полученные сечения (рис. 4.3.2). |
||||||||||
c2 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
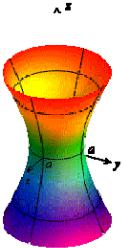
Рис. 4.3.2. Изображение однополостного гиперболоида с помощью сечений
Привычное для глаза изображение однополостного гиперболоида приведено на рисунке 4.3.3.
Рис. 4.3.3. Однополостный гиперболоид
Если в уравнении (4.3.1) a b , то сечения гиперболоида плоскостями, параллельными плоскости xOy , являются окружностями. В этом случае поверхность называется однополостным гиперболоидом вращения и может
9
быть получена вращением гиперболы, лежащей в плоскости yOz , вокруг оси
Oz (рис. 4.3.4).
Рис. 4.3.4. Однополостный гиперболоид вращения
Определение. Двуполостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
|
x2 |
|
y2 |
|
z2 |
1, |
(4.3.3) |
|
a2 |
b2 |
c2 |
||||||
|
|
|
|
|
где a,b, c – положительные числа.
Исследуем форму двуполостного гиперболоида. Так же, как эллипсоид и однополостный гиперболоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью xOy . На этой плоскости z 0, поэтому
|
x2 |
|
y2 |
1. |
|
a2 |
b2 |
||||
|
|
|
Координаты ни одной точки плоскости xOy не могут удовлетворять данному уравнению. Следовательно, двуполостный гиперболоид не пересекает эту плоскость. Найдем линию пересечения с плоскостью yOz . На этой плоскости x 0, поэтому
|
y2 |
|
z2 |
1. |
|
b2 |
c2 |
||||
|
|
|
10

Это уравнение гиперболы на плоскости yOz , где действительная полуось равна c , а мнимая полуось равна b . Построим эту гиперболу (рис. 4.3.5).
Рис. 4.3.5. Сечения двуполостного гиперболоида плоскостью yOz
Сечение плоскостью 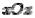 также является гиперболой, с уравнением
также является гиперболой, с уравнением
|
x2 |
|
z2 |
1. |
|
a2 |
c2 |
||||
|
|
|
Нарисуем и эту гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью yOz (рис. 4.3.6).
Найдем линии пересечения поверхности с плоскостями z h , h 0. Уравнения этих линий имеют вид
|
x2 |
|
y2 |
h2 |
||
|
|
|
|
|
|
|
|
a2 |
b2 c2 1; |
||||
|
|
|
z h. |
|||
|
|
|
||||
Очевидно, что ни одна точка не может удовлетворять этим уравнениям, |
||||||
если h c . Если h c |
или h c , |
то |
плоскость имеет с исследуемой |
|||
поверхностью только одну точку 0;0;c или 0;0; c . Эти точки называются вершинами гиперболоида.
Пусть h c . Первое уравнение преобразуем к виду
|
|
|
x2 |
|
|
|
|
|
y2 |
|
1, |
||
|
|
|
2 |
|
|
|
|
2 |
|
||||
a |
2 |
|
h |
|
|
b |
2 |
|
h |
|
|
||
|
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
2 |
|
||||
|
|
c |
|
|
|
|
c |
|
|
||||
то есть к виду
11

|
|
|
|
|
|
|
|
x2 |
|
y2 |
1, |
(4.3.4) |
|
|
|
|
|
|
|
|
a2 |
b2 |
|||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
где |
a |
a |
h2 |
1, b |
b |
h2 |
1. Уравнение (4.3.4) является |
уравнением |
||||
|
1 |
|
c2 |
1 |
|
c2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
эллипса, подобного эллипсу в плоскости |
xOy , с коэффициентом подобия |
|||||||||||
h2 |
1 |
и полуосями a |
и b . Нарисуем полученные сечения (рис. 4.3.6). |
|||||||||
c2 |
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 4.3.6. Изображение двуполостного гиперболоида с помощью сечений
Привычное для глаза изображение двуполостного гиперболоида приведено на рисунке 4.3.7.
Рис. 4.3.7. Двуполостный гиперболоид
Если в уравнении (4.3.3) a b , то сечения гиперболоида плоскостями, параллельными плоскости xOy , являются окружностями. В этом случае поверхность называется двуполостным гиперболоидом вращения и может быть получена вращением гиперболы, лежащей в плоскости yOz , вокруг оси
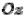 (рис 4.3.8).
(рис 4.3.8).
12

Рис. 4.3.8. Двуполостный гиперболоид
§4.4. Конус
(Конус)
Определение. Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
x2 |
|
y2 |
|
|
z2 |
0, |
(4.4.1) |
|||
|
a2 |
b2 |
|
c2 |
|||||||
|
|
|
|
|
|
|
|||||
где a,b c – положительные числа. |
|
|
|
|
|
|
|||||
Замечание. С математической точки зрения поверхность (4.4.1) лучше |
|||||||||||
определять с помощью уравнения |
|
|
|
|
|
|
|||||
|
|
|
x2 |
|
y2 |
z2, |
(4.4.2) |
||||
|
|
|
|
b2 |
|||||||
|
|
|
a2 |
|
|
|
|
||||
так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины a,b, x, y, z имеют размерность длины, то в уравнении (4.4.2)
размерности правой и левой части не согласуются.
Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью xOy . На этой плоскости z 0, поэтому
x2 y2 0. a2 b2
13
Координаты только одной точки плоскости xOy могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью yOz . На этой плоскости 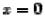 , поэтому
, поэтому
y2 z2 0. b2 c2
Это уравнение пары прямых z bc y на плоскости yOz . Построим эти прямые (рис. 4.4.1). Сечение плоскостью xOz также является парой прямых с уравнением z ac x . Нарисуем и эти прямые (рис. 4.4.1).
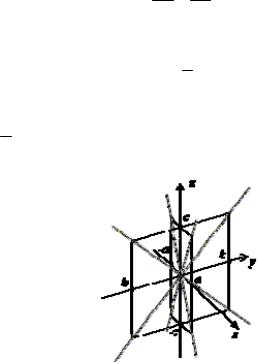
Рис. 4.4.1. Сечения конуса координатными плоскостями
Найдем линии пересечения поверхности с плоскостями z h , h 0. Уравнения этих линий
x2 |
|
|
y2 |
|
h2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
b2 |
c2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
z h. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Первое уравнение преобразуем к виду |
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|
y |
2 |
1, |
|||||
|
|
|
|
|
|
|
|
|
|
|
ah |
2 |
|
bh 2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
c |
|
|
|
|
|
|
c |
|
|
|
|||
то есть к виду |
|
|
x2 |
|
|
|
y2 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
1, |
|
|
(4.4.3) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
a2 |
b2 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
ah |
|
|
|
|
bh |
1 |
|
|
|
|
1 |
|
|
|
|
|
|
||||
где a |
, |
b |
. Уравнение (4.4.3) |
|
является уравнением эллипса. |
|||||||||||||||||||
|
|
|
||||||||||||||||||||||
1 |
|
c |
1 |
|
c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Нарисуем полученные сечения (рис. 4.4.2).
14

Рис. 4.4.2. Изображение конуса с помощью сечений
Привычное для глаза изображение приведено на рисунке 4.4.3.
Рис. 4.4.3. Конус
Точка пересечения конуса с плоскостью xOy называется вершиной конуса.
Если в уравнении (4.4.1) a b , то сечения конуса плоскостями параллельными плоскости xOy являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости yOz , вокруг оси 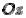 . Именно с таким конусом мы имеем дело в школьном курсе математики.
. Именно с таким конусом мы имеем дело в школьном курсе математики.
§ 4.5. Параболоиды
(Эллиптический гиперболоид) (Гиперболический параболоид)
Определение. Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
z |
x2 |
|
y2 |
, |
(4.5.1) |
|
a2 |
b2 |
|||||
|
|
|
|
15
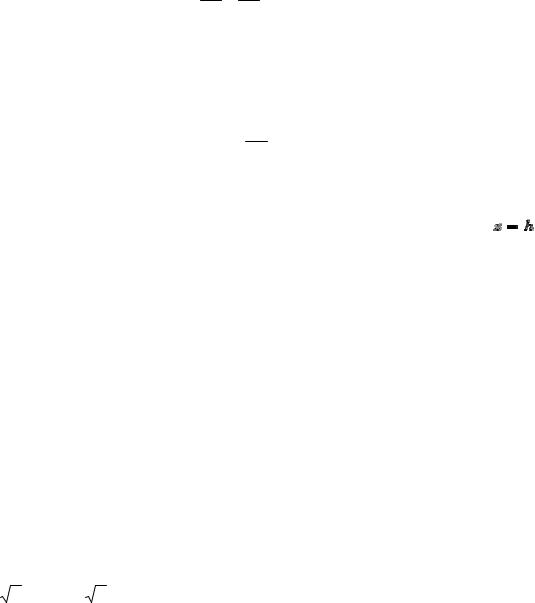
где a и b – положительные числа.
Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости xOy , yOz и координатная ось 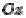 .
.
Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью xOy . На этой плоскости 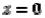 , поэтому
, поэтому
x2 y2 0. a2 b2
Координаты только одной точки плоскости xOy могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью yOz . На этой плоскости 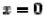 , поэтому
, поэтому
z y2 . b2
Это уравнение параболы на плоскости yOz . Построим ее (рис. 4.5.1). Сечение плоскостью xOy также является параболой. Нарисуем и ее (рис.
4.5.1). Найдем линии пересечения |
поверхности с плоскостью |
. |
|||
Уравнения этой линии |
|
|
|
|
|
x2 |
|
y2 |
|
||
|
|
|
|
|
|
a2 |
b2 h; |
|
|||
|
z h. |
|
|||
|
|
||||
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если 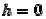 . Эта точка называется вершиной параболоида.
. Эта точка называется вершиной параболоида.
Пусть h 0. Первое уравнение преобразуем к виду
x2 |
y2 |
||
|
|
|
1 |
|
|
||
a2h |
b2h |
||
то есть к виду
|
|
x2 |
|
y2 |
1 , |
(4.5.2) |
|
|
a2 |
b2 |
|||
|
|
|
|
|
||
|
1 |
|
1 |
|
|
|
где a1 a h , |
b1 b h . Уравнение (4.5.2) является |
уравнением эллипса. |
||||
Нарисуем полученное сечение (рис. 4.5.1). При h 0 плоскость поверхность не пересекает.
16
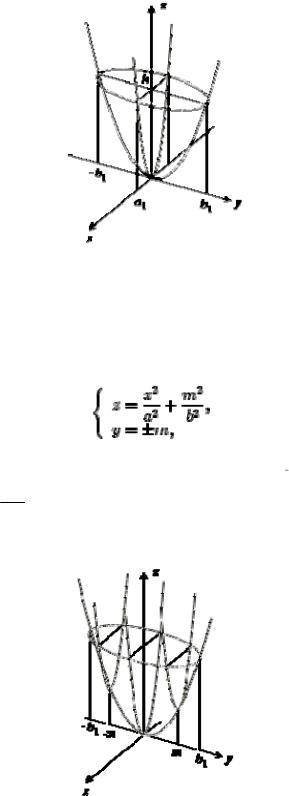
Рис. 4.5.1. Сечения эллиптического параболоида координатными плоскостями
Найдем сечения параболоида плоскостями z m , параллельными плоскости 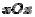 . Линии этих сечений удовлетворяют уравнениям
. Линии этих сечений удовлетворяют уравнениям
и являются параболами, такими же, как в плоскости 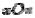 , только сдвинутыми
, только сдвинутыми
вверх на величину m2 , их вершины при таком сдвиге лежат на параболе, b2
получившейся в сечении плоскостью yOz (рис. 4.5.2).
Рис. 4.5.2. Дополнительные сечения параболоида
Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости 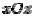 . Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости
. Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости  , а вершина скользила по параболе в плоскости yOz .
, а вершина скользила по параболе в плоскости yOz .
17

Привычное для глаза изображение приведено на рисунке 4.5.3.
Рис. 4.5.3. Эллиптический параболоид
Если в уравнении (4.5.1) a b , то сечения плоскостями, параллельными плоскости xOy , являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости yOz , вокруг оси Oz (рис. 4.5.4).
Рис. 4.5.4. Параболоид вращения
Определение. Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
z |
x2 |
|
y2 |
, |
(4.5.3) |
|
a2 |
b2 |
|||||
|
|
|
|
где a и b – положительные числа.
Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось
18
