Аналитическая геометрия

Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Пермский национальный исследовательский политехнический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

получившихся уравнений, найдем точку

получившихся уравнений, найдем точку

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

1.92 Mб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 78 / 218 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

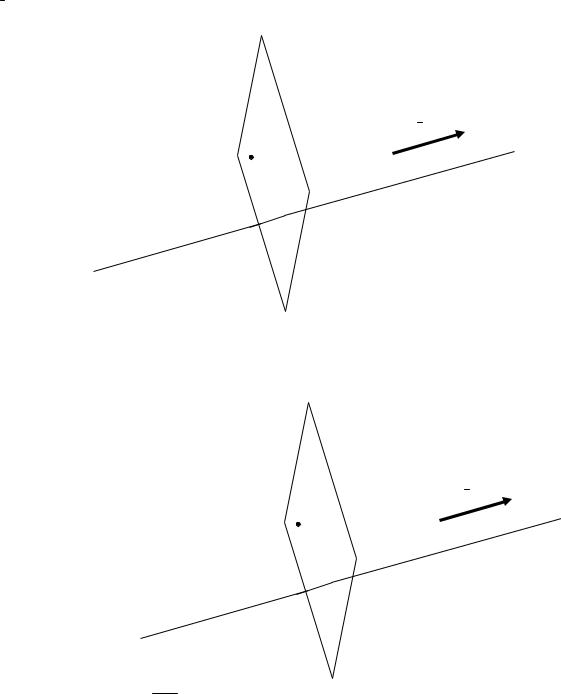
следовательно, можно определить координаты направляющего вектора прямой l 5; 4;2 . Сделаем рисунок.

Записать уравнение плоскости – значит связать координаты произвольной точки плоскости некоторым равенством. Поэтому возьмем произвольную точку плоскости M x;y;z .

Определим вектор TM .

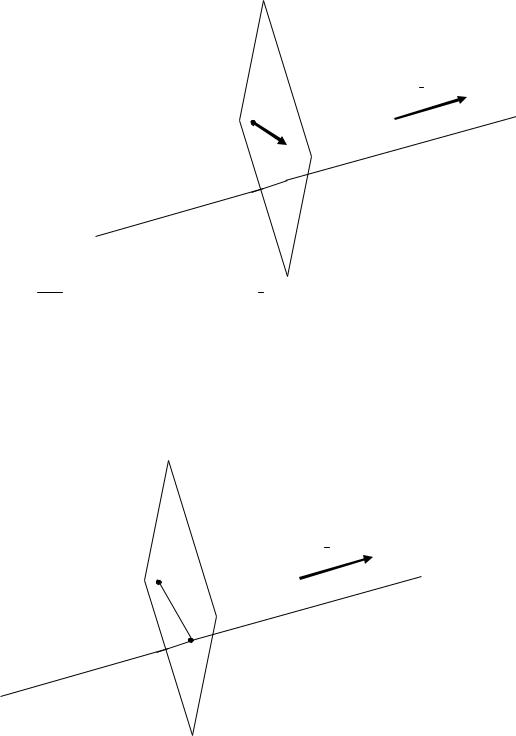
Векторы TM x 2;y 3;z 6 и l перпендикулярны, следовательно, их

скалярное произведение равно 0:
x 2 5 y 3 4 z 6 2 0		5x 4y 2z 34 0.

Последнее равенство является уравнением плоскости, проходящей через точку

Tперпендикулярно к прямой l .

2)Найдем точку пересечения полученной плоскости и заданной прямой (см. задачу 1).

Точка пересечения является решением системы

5x 4y 2z 34			0;
	x 3	y 1	z
				.
	5	4	2

Для решения системы приведем уравнение прямой к каноническому виду

5x 4y 2z 34 0;
	x 3		t;	5x 4y 2z 34 0;

		5
					x 5t 3;
	y 1
			t;		y 4t 1;
	4
					z 2t.
	z
		t;
	2

Подставив значения x;y;z в первое уравнение системы, определив значение t и сделав обратную подстановку, получим координаты точки пересечения прямой и плоскости.

																						t			1			;

		5 5t 3 4 4t 1 2 2t 34 0;																							3
																									3
																								14
										x		5t 3;								x									;
																				x					3				;
																									3
									y 4t 1;																	7
									y 4t 1;											y						7				;
																				y						3				;
											z 2t.															3
											z 2t.											z			2			.

																									3
					14		7		2																3
Полученная точка					14	;	7	;	2			является проекцией точки T на прямую l .
				P
				P			3		3
				3			3		3
3) Найдем расстояние от точки T до прямой l как расстояние от точки T
до ее проекции		P на прямую l .
T ,l			14		2								7	2		2	2	64			4		256								324	18	.
	PT	2						3							6
	PT	2	3					3					3		6	3		9			9				9						9	3


Ответ. Расстояние от точки до прямой равно																			18	.
Ответ. Расстояние от точки до прямой равно																				.
																		3
Задача 5. Записать каноническое уравнение прямой																							l : 2x y 3z 4 0;
																											x 3y z 2 0.

Решение. Линейное уравнение в пространстве определяет плоскость, т.е. два уравнения системы – это две плоскости. Решение системы – это координаты точек, принадлежащих и одной и другой плоскости, т.е. координаты точек линии пересечения. Линией пересечения двух плоскостей является прямая, таким образом данная система определяет прямую. Чтобы записать каноническое уравнение прямой нужны либо две точки, принадлежащие данной прямой, либо одна точка и направляющий вектор. Поэтому возможны два способа решения задачи.

СПОСОБ 1. Найдем две точки, принадлежащие заданной прямой. Координаты искомых точек будут являться решениями данной системы. В системе два уравнения с тремя неизвестными, следовательно, решений системы бесконечно много. Чтобы получить какое-нибудь одно решение необходимо придать какой-либо неизвестной конкретное значение.

Пусть, например, x 0, тогда система примет вид:

2 0 y 3z 4 0;

y 3z 4 0;

y 3z 4;

;

0 3y z 2 0;

3y z 2

3 3z 4 z 2 0;

Пусть теперь y 0, тогда система примет вид

2x 0 3z 4 0;

2x 3z 4 0;

2 2

z 3z 4

z 0;

x z 2 0;

x 2 z;

x 3 0 z 2

x 2.

Таким

образом, заданная прямая

проходит через точки

;

A 0;

B 2;0;0 . Запишем уравнение прямой. Сделаем рисунок.

Записать уравнение прямой – значит связать некоторым равенством координаты произвольной точки прямой. Поэтому возьмем произвольную точку прямой M x;y;z .

Определим векторы AM и AB .

Векторы	AM	и			AB		коллинеарны,											следовательно,											их координаты
пропорциональны:
										1					5									1		;z		5	;
										1					5									1				5
			AM x 0;y								;z									x;y
			AM x 0;y							4	;z				4					x;y				4				4
										4					4									4				4
												1					5					1			;		5	;
												1					5					1					5
				AB 2				0;0						;0						2;
				AB 2				0;0				4		;0						2;		4					4
												4					4					4		5			4
																		1						5
														x		y					z					.
																			4						4
						AM			AB


													2					1				5
													2					1				5

																		4					4

Последнее равенство является каноническим уравнением заданной прямой.

СПОСОБ 2. Найдем координаты какой-либо точки заданной прямой, как это описано в способе 1. Возьмем, например, x 0 и, решив систему

Найдем направляющий вектор прямой. Направляющих векторов у прямой бесконечное множество. Нам нужен какой-нибудь один. Плоскости, определяющие прямую, заданы общими уравнениями, по которым можно

определить координаты нормальных векторов этих плоскостей: N1 2; 1;3 и N2 1; 3;1 . Вектор N1 перпендикулярен плоскости 2x y 3z 4 0, прямая l лежит в этой плоскости, следовательно, вектор N1 перпендикулярен прямой l .

Вектор	N2	перпендикулярен плоскости x 3y z 2 0, прямая l					лежит в этой
плоскости,		следовательно, вектор		перпендикулярен		прямой l .		Таким
			N2
образом,		прямая l перпендикулярна		и вектору		и	вектору			.
					N1				N2

Направляющий вектор прямой параллелен прямой, следовательно, будет

перпендикулярен

векторам

. Поэтому в качестве направляющего

вектора прямой можно взять векторное произведение векторов

i 1 1 3 3

2 1 3 1

2 3 1 1 8i

Получаем координаты направляющего вектора прямой l 8;1; 5 .

Таким образом, известна точка					1		5	, принадлежащая прямой, и
			A 0;			;
			A 0;		4	;	4
					4		4
направляющий вектор прямой		8;1; 5 .		Запишем каноническое уравнение
направляющий вектор прямой	l	8;1; 5 .		Запишем каноническое уравнение

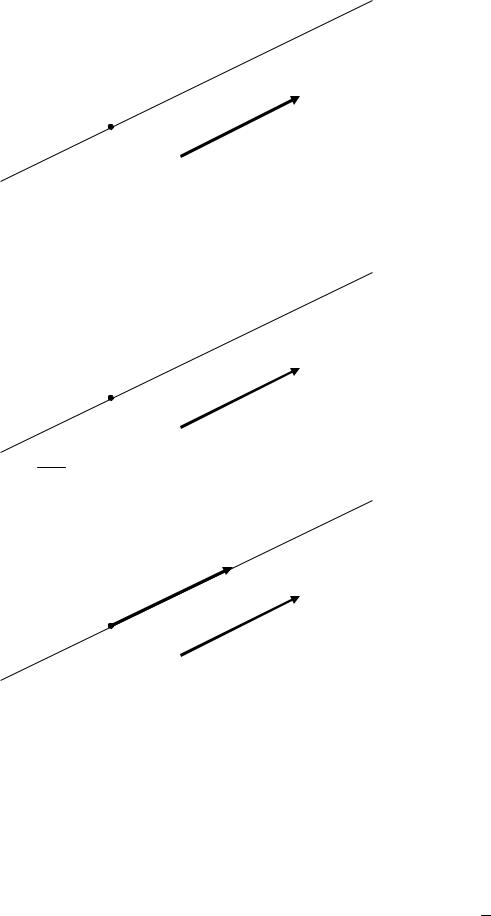
прямой. Сделаем рисунок.

A	l

Записать уравнение прямой – значит связать координаты произвольной точки прямой некоторым равенством. Поэтому возьмем произвольную точку прямой M x;y;z .

A	l

Определим вектор AM .


A	l
A

		1		5
Векторы		1		5	и		l коллинеарны, следовательно, их координаты
	AM x;y		;z
	AM x;y	4	;z	4
		4		4
пропорциональны:									1	5
									1	5
						x		y			z		.
						x		y	4		z	4
					8
					8		1				5

Полученное равенство является каноническим уравнением заданной прямой. Замечание. На первый взгляд уравнения, полученные при решении задачи

различными способами различны, но если взять уравнение прямой, полученное при решении способом 1 и умножить все его части (ссылка) на число 14 , то получим уравнение из способа 2.

Ответ. Каноническое уравнение заданной прямой имеет вид

x		y	1	z	5
			4		4	.
8
	1			5

Задачи к главе 2

2.1. Записать каноническое уравнение прямой

2.1.1. 3x y 2z 4 0;		2.1.2. x 3y 2z 2 0;
2x y z 8 0		x 3y z 14 0
2.1.3. x 2y z 4 0;		2.1.4. x y z 2 0;
2x 2y z 8 0		x y 2z 2 0
2.1.5. 2x 3y z 6 0;		2.1.6. 3x y z 6 0;
x 3y 2z 3 0		3x y 2z 0
2.1.7. x 5y 2z 11 0;		2.1.8. 5x y 3z 4 0;
	x y z 1 0	x y 2z 2 0
2.1.9. 3x 4y 2z 1 0;		2.1.10. x y z 2 0;
2x 4y 3z 46 0		x 2y z 4 0
2.1.11. 4x y 3z 2 0;		2.1.12. 6x 7y 4z 2 0;
	2x y z 8 0	x 7y z 5 0
2.1.13. 3x 3y 2z 1 0;		2.1.14. 8x y 3z 1 0;
	2x 3y z 6 0	x y z 10 0
2.1.15. 6x 5y 4z 8 0;		2.1.16. x 5y z 5 0;
	6x 5y 3z 4 0	2x 5y 2z 5 0
2.1.17. 2x 3y z 6 0;		2.1.18. 5x y 2z 4 0;
	x 3y 2z 3 0	x y 3z 2 0
2.1.19. 4x y z 2 0;		2.1.20. 2x y 3z 2 0;
	2x 3y z 6 0	2x y z 6 0
2.1.21. x y 2z 2 0;		2.1.22. x 5y z 11 0;
	x y z 2 0	x y 2z 1 0
2.1.23. x y z 2 0;		2.1.24. 6x 7y z 2 0;
	x 2y z 4 0	x 7y 4z 5 0
2.1.25. x 5y 2z 5 0;		2.1.26. x 3y z 2 0;
	2x 5y z 5 0	x 3y 2z 14 0
2.1.27. 2x 3y 2z 6 0;		2.1.28. 3x 4y 3z 1 0;
	x 3y z 3 0	2x 4y 2z 4 0
2.1.29. 3x 3y z 1 0;		2.1.30. 6x 5y 3z 8 0;
	2x 3y 2z 6 0	6x 5y 4z 4 0

2.2. Найти расстояние от точки A , заданной координатами, до прямой l , заданной каноническим уравнением.

2.2.1. A 0; 3; 2		l :	x 1		y 1,5												z
2.2.1. A 0; 3; 2		l :	1		1											2
			1		1											2
2.2.2. A 0; 1;1		l :	x 4,5			y 3												z 2
2.2.2. A 0; 1;1		l :	1			0,5													1
			1			0,5													1
2.2.3. A 1;1;1 l :	x 2		y 1,5			z 1
2.2.3. A 1;1;1 l :			2				1
1			2				1
2.2.4. A 1;2;3		l :	x 0,5			y 1,5														z 1,5
2.2.4. A 1;2;3		l :	0				1												1
			0				1												1
2.2.5. A 1;0; 1		l :	x 3,5			y 1,5														z
2.2.5. A 1;0; 1		l :	2																0
			2				2												0
2.2.6. A 2;1;0		l :	x 2		y 1,5													z 0,5
2.2.6. A 2;1;0		l :	0			1
			0			1													1
2.2.7. A 2; 3;0		l :	x 0,5			y 1,5														z 0,5
2.2.7. A 2; 3;0		l :	1				1
			1				1												2
2.2.8. A 1;0; 1		l :	x	y 1,5							z 2
2.2.8. A 1;0; 1		l :
			1		0											2
2.2.9. A 0;2; 2		l :	x 1		y				z 1

			2		1
			2		1					3
2.2.10. A 3; 3; 1		l :	x 6		y 3,5													z 1,5
2.2.10. A 3; 3; 1		l :	5			4													0
			5			4													0
2.2.11. A 3;3;3		l :	x 1		y 1,5												z 3
2.2.11. A 3;3;3		l :	1			0													2
			1			0													2
2.2.12. A 1;2;0		l :	x 0,5			y 1												z 2
2.2.12. A 1;2;0		l :	2			3													2
			2			3													2
2.2.13. A 2; 2; 3		l :	x 1		y 2									z 1
2.2.13. A 2; 2; 3		l :	1		3
			1		3											2
2.2.14. A 3;0;1		l :	x 2		y				z 1
2.2.14. A 3;0;1		l :	2		3
			2		3					2
2.2.15. A 1; 1; 2		l :	x 1		y 2									z
2.2.15. A 1; 1; 2		l :	4		3
			4		3					1
2.2.16. A 1; 1;2		l :	x 3		y 5									z
2.2.16. A 1; 1;2		l :	1		2
			1		2					2
2.2.17. A 2; 1;1		l :	x 2		y				z 1
2.2.17. A 2; 1;1		l :	0		3
			0		3					2
2.2.18. A 1;1; 4		l :	x 1		y 5								z 1
2.2.18. A 1;1; 4		l :	2		3										2
			2		3										2
2.2.19. A 1; 2;0		l :	x 1		y			z 5

			3		1
			3		1					2
2.2.20. A 1;3;1		l :	x 1		y 2							z 3
2.2.20. A 1;3;1		l :	4		1
			4		1										2
2.2.21.A 1;3; 1		l :	x 1		y 1						z 3
2.2.21.A 1;3; 1		l :	2		3
			2		3											2

2.2.22. A 3; 1;2

l :

x 1

y 1

2.2.23. A 2;3; 1

l :

x 1

y 4

2.2.24. A 4; 1;0

l :

x 1

y 1,5

2.2.25. A 2; 1;1

l :

x 2

y 5

2.2.26. A 1;1; 2

l :

x 5

y 7

z 2

2.2.27. A( 1;1;2)

l :

x 1

y 2

z 1

2.2.28. A( 3;1;7)

l :

x 3

y 7

z 1

2.2.29.A( 3;2;1) l : x 5 y 3 z 3

2 4 1

2.2.30. A 1;0; 2	l :	x 2	y 7	z 6
				3
	4

2.3. Решить задачи.

2.3.1. Записать уравнение плоскости , проходящей через точки А(–1;5;2),

В(3;–1;3) и С(0;3;0).

2.3.2.Записать уравнение плоскости , проходящей через точку А(–3;1;-2) параллельно векторам a { 4;5;3} и b { 2;7;9}.

2.3.3.Записать уравнение плоскости, проходящей через точки A( 1;1;2) и

B(3; 1;4) параллельно вектору a 5;2;3 .

2.3.4.Записать уравнение плоскости , проходящей через точки А(–1;3;5) и В(2;–4;1) параллельно вектору с { 4;1;0}.

2.3.5.Записать уравнение прямой, проходящей через точку А(–1;1;8) параллельно вектору с { 4;7;1}.

2.3.6.Записать уравнение прямой, проходящей через точку C(3; 2;3) перпендикулярно плоскости 2x 3y 7z 0.

2.3.7.Записать уравнение плоскости, проходящей через точку A( 1;1;2)

перпендикулярно к прямой x 1 y 2 z 1.

3 2

2.3.8. Записать уравнение прямой, проходящей через точку A( 3;1;7) перпендикулярно к плоскости 4x y 3z 5 0.

2.3.9.Записать уравнение плоскости , проходящей через точку B(3;1; 1) параллельно плоскости :6x 2y 7z 4 0.

2.3.10.Записать уравнение плоскости, проходящей через точку A( 3;2;1)

параллельно прямой	x 3	y 7	z 1 и вектору		3; 1;2 .
				c
	4	2

2.3.11. Записать уравнение плоскости, проходящей через точки A( 3;2;1) и

C(1; 1;5) параллельно прямой

x 3

y 7

z 1.

2.3.12. Записать уравнение плоскости, проходящей через точку C( 2;3;7)

перпендикулярно к прямой

x 5

y 3

z 3

2.3.13. Записать уравнение прямой, проходящей через точку А(–1;1;1)

параллельно прямой

x 2

y 3

z 5.

2.3.14. Записать уравнение плоскости , проходящей через точку А(–3;6;1)

параллельно прямым	x 2	y 7	z 6	и	x 5	y 3	z 3	.
	4		3		2	4	1

2.3.15. Найти расстояние от точки Т(3;2;7) до плоскости , проходящей через

точку A( 1;1;2)перпендикулярно к прямой	x 1	y 3	z 5	.
	2	4
			3

2.3.16.Найти расстояние между плоскостями 2x 3y z 4 0 и

4x 6y 2z 3 0.

2.3.17.Найти расстояние между плоскостями 4x y z 7 0 и 8x 2y 2z 9 0.

2.3.18. Найти расстояние от прямой	x 2	y 7	z 6	до плоскости
	4		3
x 2y 2z 7 0.

2.3.19.Записать уравнение плоскости, проходящей через точку С(–2;5;1) параллельно плоскости :3x 5y z 7 0.

2.3.20.Записать уравнение прямой, проходящей через точку P( 2;3; 1) параллельно плоскостям 4x y z 3 0 и 2x 5y 2z 3 0.

2.3.21.Записать уравнение прямой, проходящей через точку Q( 1;1;8) перпендикулярно к плоскости 4x 3y 2z 1 0.

2.3.22.Записать уравнение плоскости, проходящей через точки D(2; 4;3) и

K( 5;1;3) параллельно прямой

x 3

y 1

z 2

2.3.23. Записать уравнение плоскости, проходящей через точку C( 2;2;4)

параллельно вектору

{ 2;7;9} и прямой

x 3

y 1

z 2

2.3.24. Найти расстояние между прямой

x 1

y 3

z 5

и плоскостью

2x 5y 8z 1 0.

x 2

z 6

x 1

y 3

z 5

2.3.25. Могут ли прямые

y 7

лежать в одной

плоскости?

2.3.26. Записать уравнение плоскости, которой принадлежат прямые

x 5

y 3

z 3

x 1

y 2

z 4

<<< < Предыдущая 1 2 3 4 5 6 78 / 218 9 10 11 12 13 14 15 16 17 18 19 20 21 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
15.11.20222.57 Mб2Анализ научных результатов Пермского политехнического университета..pdf
#
15.11.20221.59 Mб9Анализ финансовой деятельности..pdf
#
15.11.202224.51 Mб16Анализ хозяйственной деятельности предприятия.-1.pdf
#
15.11.202224.53 Mб15Анализ хозяйственной деятельности предприятия..pdf
#
15.11.20223 Mб19Аналитика. Электрохимические методы анализа.pdf
#
15.11.20221.92 Mб2Аналитическая геометрия..pdf
#
15.11.20221.37 Mб20Аналитическая динамика и теория колебаний. Исследование динамики мех.pdf
#
15.11.20221.8 Mб14Аналитические и численные методы решения дифференциальных уравнений ..pdf
#
15.11.2022496.15 Кб11Аналитические методы в биохимии и биотехнологии..pdf
#
15.11.20225.76 Mб7Английская поэзия XIV–XX веков..pdf
#
15.11.20221.08 Mб3Антикризисное управление..pdf