
Аналитическая геометрия
..pdf
Задача 2.Выполнив последовательно преобразования координат: поворот, а затем параллельный перенос координатных осей, преобразовать к каноническому виду уравнение кривой второго порядка и построить ее в исходной системе координат, а также найти параметры кривой. Провести исследование кривой при помощи инвариантов преобразования.
2.1. |
3x 2 4xy 4 0 |
|
2.2. |
13x 2 10xy 13y 2 18 |
2x 54 0 |
2.3.x 2 2xy y 2 2x 2y 4 0
2.4.x 2 4xy y 2 6x 6y 6 0
2.5. |
3x 2 10xy 3y 2 24 |
2x 24 |
2y 64 0 |
|
2.6. |
x 2 xy y 2 |
2x |
2y 1 0 |
|
2.7.2xy 4x 2y 3 0
2.8.4xy 3y 2 4y 36 0
2.9.5x 2 4xy 8y 2 36 0
2.10. x 2 2xy y 2 2 |
2x 2 |
2y 4 0 |
2.11. 3x 2 6xy 3y 2 |
2 |
2x 2 2y 20 0 |
|||
2.12. |
4x 2 |
24xy 11y 2 24x 2y 19 0 |
|||
2.13. |
4x 2 |
8xy 4y 2 |
|
2x |
2y 4 0 |
2.14.4xy 3y 2 4x 6y 33 0
2.15.3x 2 4xy 3y 2 6x 4y 2 0
2.16. 13x 2 6 3xy |
7y 2 48 |
3x 48y 144 0 |
|||
2.17. x 2 2xy y 2 |
2 |
2x 2 |
2y 8 0 |
||
2.18. 5x 2 8xy 5y 2 20x 16y 11 0 |
|||||
2.19. 3x 2 10xy 3y 2 2 2x 2 |
2y 6 0 |
||||
2.20. 5x 2 |
8xy 5y 2 |
2x |
2y 4 0 |
||
2.21. 5x 2 |
2 3xy 3y 2 |
10x 2 |
3y 7 0 |
||
2.22. 5x 2 |
6xy 5y 2 8 2x 8 |
2y 0 |
|||
2.23. 5x 2 |
2 3xy 3y 2 |
2 3x 6y 9 0 |
|||
2.24.7x 2 48xy 7y 2 40x 30y 75 0
2.25.5x 2 8xy 5y 2 8x 10y 4 0
2.26.18x 2 48xy 32y 2 20x 15y 100 0
2.27.5x 2 8xy 5y 2 20x 16y 11 0
2.28. |
5x 2 8xy 5y 2 |
|
2x |
2y 4 0 |
2.29. |
4x 2 8xy 4y 2 |
|
2x |
2y 4 0 |
2.30. x 2 3xy 3y 2 7x 14 0
30
31
Оглавление
Оглавление............................................................................................ |
1 |
4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА.................................... |
2 |
§4.1. Сфера.......................................................................................... |
2 |
§4.2. Эллипсоид.................................................................................. |
4 |
§4.3. Гиперболоиды........................................................................... |
7 |
§4.4. Конус ........................................................................................ |
13 |
§ 4.5. Параболоиды.......................................................................... |
15 |
§4.6. Цилиндры................................................................................ |
22 |
§4.7. Параллельный перенос системы координат .................... |
25 |
§ 4.8. Задачи к главе 4..................................................................... |
28 |
1

4. ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА
Поверхности, декартовы прямоугольные координаты точек которых удовлетворяют алгебраическому уравнению 2-й степени:
a |
x2 a |
22 |
y2 a |
33 |
z2 2a |
xy 2a |
xz 2a |
23 |
yz b x b |
y b |
z c 0 (4.1) |
|
11 |
|
|
12 |
13 |
|
1 |
2 |
2 |
|
|||
Уравнение (4.1) может и не определять действительного геометрического образа, но для сохранения общности в таких случаях говорят, что оно определяет мнимую поверхность второго порядка. В зависимости от значений коэффициентов общего уравнения (4.1) оно может быть преобразовано с помощью параллельного переноса и поворота системы координат к одному из канонических видов, каждому из которых соответствует определённый класс поверхностей второго порядка. Среди них выделяют пять основных типов поверхностей. Именно, эллипсоиды, гиперболоиды, параболоиды, конусы второго порядка, цилиндры второго порядка.
§4.1. Сфера
Определение. Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.
Запишем уравнение сфера радиуса 
 с центром в точкеM 0 x0;y0;z0 .
с центром в точкеM 0 x0;y0;z0 .
Записать уравнение сферы – значит связать координаты произвольной точки сферы некоторым равенством. Поэтому возьмем произвольную точку сферы M x;y;z . По определению сферы MM 0 R . Поскольку
MM 0  x x0 2 y y0 2 z z0 2 ,
x x0 2 y y0 2 z z0 2 ,
то уравнение сферы имеет вид
x x0 2 y y0 2 z z0 2 R |
|
|
или |
|
|
x x0 2 y y0 2 z z0 2 |
R2. |
(4.1.1) |
Пример. Нарисуйте сферу x2 y2 z2 2x 4y 2z 2 0.
Решение. Выделив полные квадраты
x2 2x y2 4y z2 2z 2 0,
x2 2x 1 1 y2 4y 4 4 z2 2z 1 1 2 0,
x 1 2 1 y 2 2 4 z 1 2 1 2 0,
2
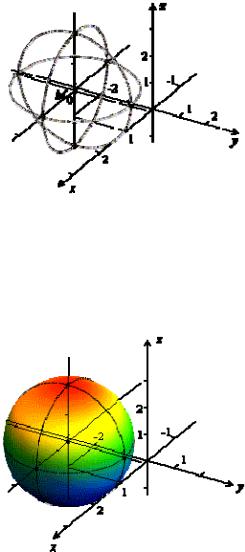
получим
x 1 2 y 2 2 z 1 2 4.
Значит, центром сферы является точка M 0 1; 2;1 , радиус сферы равен 2.
Для ее изображения нарисуем сечения сферы плоскостями, проходящими через центр и параллельными координатным плоскостям. Каждое такое сечение будет окружностью радиуса 2 с центром в точке M 0
(рис 4.1.1).
Рис. 4.1.1. Сфера, изображенная сечениями
Более "художественное" изображение сферы приведено на рисунке
Рис. 4.1.2. Сфера
3
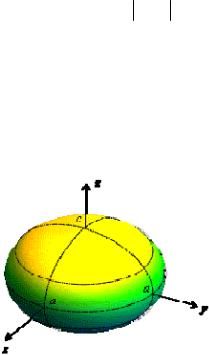
§4.2. Эллипсоид
(Эллипсоид)
Определение. Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид
|
x2 |
|
y2 |
|
|
z2 |
1, |
(4.2.1) |
||||||||||||
|
a2 |
b2 |
|
c2 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
где a,b, c – положительные числа. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Исследуем форму эллипсоида. Из уравнения видно, что координаты |
||||||||||||||||||||
точек поверхности ограничены: |
|
x |
|
a , |
|
|
y |
|
b , |
|
|
z |
|
c . |
||||||
|
|
|
|
|
|
|||||||||||||||
Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат.
Для выяснения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью xOy . Так как любая точка плоскости xOy имеет нулевую третью координату,  , то координаты точек эллипсоида на плоскости xOy удовлетворяют уравнению
, то координаты точек эллипсоида на плоскости xOy удовлетворяют уравнению
x2 |
|
y2 |
1. |
(4.2.2) |
|
a2 |
b2 |
||||
|
|
|
Т.е. линия пересечения является эллипсом с полуосями a и b (рис. 4.2.1).
Рис. 4.2.1. Сечение плоскостью xOy
Аналогично, сечение в плоскости yOz дает эллипс
y2 z2 1 b2 c2
с полуосями b и c , а сечение плоскостью xOz – эллипс
4
x2 z2 1 a2 c2
с полуосями a и c (рис.4.2.2).
Рис. 4.2.2. Сечения эллипсоида координатными плоскостями
Нарисованный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью  . Эта плоскость параллельна плоскости xOy и пересекает ось
. Эта плоскость параллельна плоскости xOy и пересекает ось  в точке
в точке 
 . Уравнение этой линии имеет вид
. Уравнение этой линии имеет вид
x2 |
|
|
y2 |
|
z2 |
1; |
|
x2 |
|
y2 |
|
h2 |
|
|
|
|
|
|
|
|
|
1 |
. |
||||||
|
|
|
|
|||||||||||
a2 |
|
|
b2 |
|
c2 |
|
|
|
|
|||||
|
|
|
|
a2 |
b2 |
c2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
z h; |
|
|
|
|
|
|
|
|
|
|
|
|||
Очевидно, что если h c , то ни одна точка пространства не может
удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой – отрицательное.
Если h c , то сечении получим лишь одну точку 0;0;c или 0;0; c в зависимости от знака h .
Пусть h c . Тогда последнее уравнение можно преобразовать к виду
x2 |
|
|
|
|
y2 |
|
|
|
1. |
||
|
|
h2 |
|
|
h2 |
||||||
a2 1 |
|
|
|
|
b2 1 |
|
|
|
|
||
|
2 |
|
2 |
||||||||
|
|
c |
|
|
|
c |
|
||||
|
|
|
|
|
|
|
|
||||
|
|
|
h2 |
|
|
|
h2 |
|
||||
Обозначив a2 |
a2 1 |
|
|
|
|
, b2 |
b2 1 |
|
|
|
|
, получим уравнение |
|
2 |
|
2 |
|||||||||
1 |
|
|
c |
|
1 |
|
|
c |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||
5
|
|
|
x |
2 |
|
y2 |
1. |
|
|
(4.2.3) |
|
|
|
|
a |
2 |
b2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
1 |
|
|
|
|
|
||
Уравнение (4.2.3) |
является уравнением эллипса, |
подобного |
эллипсу, |
||||||||
задаваемому |
уравнением (4.2.2), |
|
с |
коэффициентом |
подобия |
1 |
h2 |
и |
|||
|
c2 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
полуосями a1 |
и b1. Ясно, что сечение плоскостью z h является таким же |
||||||||||
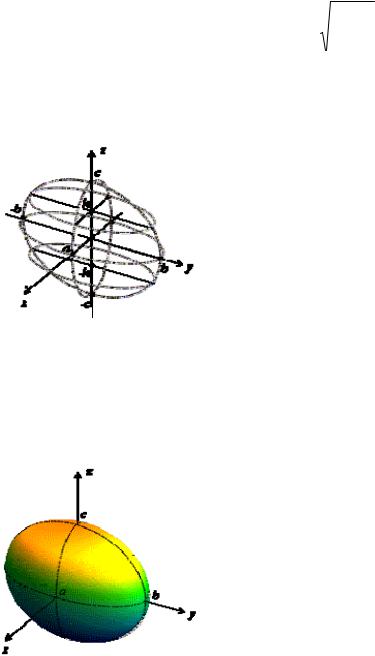
эллипсом, расположенным симметрично первому относительно плоскости xOy . Нарисуем эти сечения (рис. 4.2.3).
Рис. 4.2.3. Дополнительные сечения эллипсоида
Таким образом, весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости xOy и подобных эллипсу в плоскости xOy . Рисунок 4.2.4 дает более привычное глазу изображение эллипсоида.
Рис. 4.2.4.Эллипсоид
Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии – центром эллипсоида. Числа a,b, c называются полуосями. Если
полуоси попарно различны, то эллипсоид называется трехосным.
Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен
6
вращением эллипса вокруг одной из осей. Например, если a b , то все сечения эллипсоида плоскостями z h , h c , будут окружностями. Сам
эллипсоид может быть получен из эллипса
y2 |
|
z2 |
1, b a , |
|
a2 |
c2 |
|||
|
|
лежащего в плоскости yOz , при вращении его вокруг оси Oz (рис. 4.2.5).
Рис. 4.2.5.Эллипсоид вращения
§4.3. Гиперболоиды
(Однополостный гиперболоид) (Двуполостный гиперболоид)
Определение. Однополостным гиперболоидом называется поверхность, каноническое уравнение которой имеет вид
x2 |
|
y2 |
|
z2 |
1 |
(4.3.1) |
|
a2 |
b2 |
c2 |
|||||
|
|
|
|
где a,b, c – положительные числа.
Исследуем форму однополостного гиперболоида. Так же, как эллипсоид, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения гиперболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью xOy . На этой плоскости z 0, поэтому
x2 |
|
y2 |
1. |
|
a2 |
b2 |
|||
|
|
7
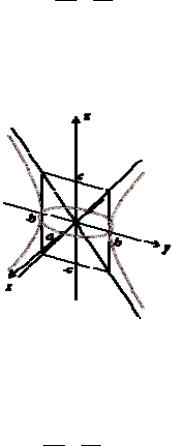
Это уравнение на плоскости xOy задает эллипс с полуосями a и b (рис. 4.3.1). Найдем линию пересечения с плоскостью yOz . На этой плоскости x 0, поэтому
y2 z2 1. b2 c2
Это уравнение гиперболы на плоскости yOz , где действительная полуось равна b , а мнимая полуось равна c . Построим эту гиперболу (рис. 4.3.1).
Рис. 4.3.1. Сечения однополостного гиперболоида двумя плоскостями
Сечение плоскостью xOz также является гиперболой с уравнением
x2 z2 1. a2 c2
Нарисуем и эту гиперболу, но чтобы не перегружать чертеж дополнительными линиями, не будем изображать ее асимптоты и уберем асимптоты в сечении плоскостью yOz (рис. 4.3.2).
Найдем линии пересечения поверхности с плоскостями z h , h 0. Уравнения этих линий имеют вид
x2 |
|
y2 |
h2 |
|||
|
|
|
|
|
|
|
|
b2 1 c2 ; |
|||||
a2 |
||||||
|
|
z h. |
|
|
||
|
|
|
|
|||
Первое уравнение преобразуем к виду
x2 |
|
|
|
|
y2 |
|
|
|
1, |
||
|
|
h2 |
|
|
h2 |
||||||
a2 1 |
|
|
|
|
b2 1 |
|
|
|
|
||
|
2 |
|
2 |
||||||||
|
|
c |
|
|
|
c |
|
||||
|
|
|
|
|
|
|
|
||||
то есть к виду
8
