
Аналитическая геометрия
..pdfОглавление |
|
Оглавление ................................................................................................ |
1 |
1. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ...................................... |
2 |
§1.1. Уравнение прямой, проходящей через две данные точки......... |
2 |
§1.2. Каноническое уравнение прямой................................................ |
3 |
(Уравнение прямой, проходящей через данную точку ...................... |
3 |
параллельно данному вектору)............................................................. |
3 |
§1.3. Общее уравнение прямой............................................................. |
6 |
(Уравнение прямой, проходящей через данную точку ...................... |
6 |
перпендикулярно к данному вектору) ................................................. |
6 |
§1.4. Нормальное уравнение прямой ................................................. |
12 |
(уравнение прямой, находящейся на расстоянии p от начала |
|
координат, нормаль к которой составляет угол с положительным |
|
направлением действительной оси)................................................... |
12 |
§1.6. Расстояние от точки до прямой................................................. |
15 |
§1.7. Уравнение прямой через угловой коэффициент...................... |
18 |
§1.8. Уравнение прямой в отрезках.................................................... |
20 |
§1.9. Взаимное расположение прямых на плоскости....................... |
21 |
§1.10. Уравнение линии в полярной системе координат ................. |
27 |
Задачи к главе 1.................................................................................... |
30 |
1

1. УРАВНЕНИЕ ПРЯМОЙ НА ПЛОСКОСТИ
§1.1. Уравнение прямой, проходящей через две данные точки
(Прямая на плоскости. Способы задания)
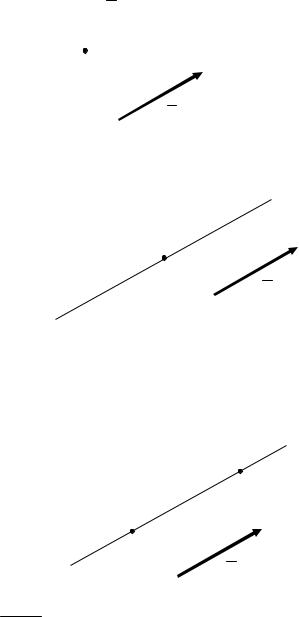
Пусть даны две точки M1 x1;y1 и M 2 x2;y2 . Необходимо записать уравнение прямой M1M 2 . Сделаем рисунок.
M1
M 2
Записать уравнение прямой – это значит связать координаты произвольной точки прямой некоторым равенством. Поэтому возьмем произвольную точку прямой M x;y :
M
M1
M 2
Определим векторы M1M и M1M 2 :
M
 M1
M1
M 2
Векторы M1M и M1M 2 коллинеарны, следовательно, их координаты пропорциональны. Найдем (коордвекторапл):
M1M x x1;y y1 ; M1M 2 x2 x1;y2 y1 .
Запишем условие коллинеарности:
2
x x1 |
|
y y1 |
. |
||||
|
|
||||||
x |
2 |
x |
|
y |
2 |
y |
|
|
1 |
|
|
1 |
|
||
Полученное равенство и является уравнением прямой, проходящей через две данные точки.
§1.2. Каноническое уравнение прямой
(Уравнение прямой, проходящей через данную точку
параллельно данному вектору)
(Прямая на плоскости. Способы задания)
Даны точка M 0 x0;y0 и вектор p p1; p2 :
M 0
p
Проведем через данную точку прямую параллельно данному вектору:
M 0
p
Записать уравнение прямой – это значит связать некоторым равенством координаты произвольной точки прямой. Поэтому возьмем произвольную точку прямой M x;y :
M
M 0
p
Определим вектор M 0M :
3

M
M 0
p
Векторы M 0M и p коллинеарны, следовательно, их координаты пропорциональны. Найдем координаты вектора M 0M :
M 0M x x0;y y0 .
Запишем условие коллинеарности:
x x0 y y0 . p1 p2
Полученное равенство является уравнением прямой, проходящей через данную точку параллельно данному вектору.
ВАЖНО:
1)Полученное уравнение называется каноническим уравнением прямой.
2)Вектор p называется направляющим вектором прямой.
3)В каноническом уравнении прямой числа, стоящие в знаменателе определяют координаты направляющего вектора.
Пример. Записать уравнение прямой, проходящей через точку A 2; 7
параллельно прямой l : x 41 y 53.
Решение. Изобразим данные задачи на рисунке. Дана точка A, прямая l .
Проверим, лежит ли точка A на прямой l . Для этого необходимо подставить координаты точки A в уравнение прямой l . Если получится верное равенство, то точка лежит на прямой, если не верное, то точка не лежит на прямой. При
подстановке получаем: |
2 1 |
|
7 3 |
или, после преобразований, |
1 |
2. |
|
4 |
|
5 |
4 |
||||
|
|
|
A не лежит на прямой l . |
|
|||
Равенство неверно, следовательно, точка |
|
|
|||||
l
A
4
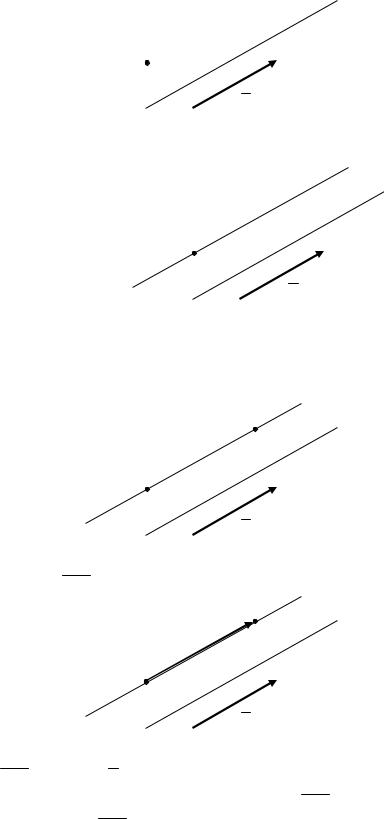
Прямая l задана каноническим уравнением, следовательно, можно указать направляющий вектор прямой, координатами которого являются числа, стоящие в знаменателях дробей в левой и правой частях уравнения, т.е.
p 4; 5 – направляющий вектор прямой l .
l
A
p
Проведем через точку A прямую параллельно прямой l :
l
A
p
Записать уравнение прямой – значит связать некоторым равенством координаты произвольной точки прямой. Поэтому возьмем произвольную точку M x;y на искомой прямой:
M
l
A
p
Определим вектор AM :
M
l
A
p
Векторы AM и p коллинеарны, следовательно, их координаты
пропорциональны. Найдем координаты вектора AM :
AM x 2;y 7 x 2;y 7 .
5
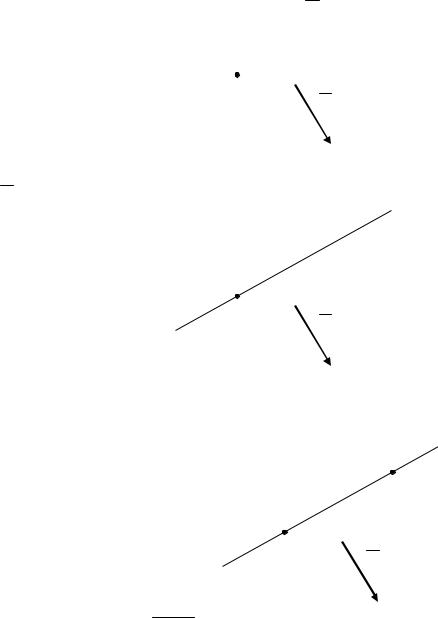
Запишем условие коллинеарности векторов:
x 2 |
|
y 7 |
|
|
|
|
. |
4 |
5 |
||
Полученное уравнение является каноническим уравнением искомой прямой.
§1.3. Общее уравнение прямой
(Уравнение прямой, проходящей через данную точку
перпендикулярно к данному вектору)
(Прямая на плоскости. Способы задания)
Даны точка M 0 x0;y0 и вектор N A;B :
M0 N
Проведем через точку M 0 x0;y0 прямую перпендикулярно к вектору
N A;B :
M0 N
Записать уравнение прямой – это значит связать координаты произвольной точки прямой некоторым равенством. Поэтому возьмем произвольную точку прямой M x;y :
M
M0 N
Определим вектор M 0M :
6

M
M0 N
Векторы M 0M и N перпендикулярны, следовательно, их скалярное произведение равно 0. Найдем координаты вектора M 0M :
M 0M x x0;y y0 .
Запишем условие перпендикулярности:
M 0M N 0 A x x0 B y y0 0.
Последнее равенство и является искомым уравнением. После преобразований,
получим: Ax By Ax0 By0 0.
Обозначив Ax0 By0 C , получим уравнение
Ax By C 0.
ВАЖНО:
1)Полученное уравнение называется общим уравнением прямой.
2)Вектор N называется нормальным вектором прямой.
3)В общем уравнении прямой коэффициенты при x и y определяют
координаты нормального вектора.
Пример. Записать уравнение прямой, проходящей через точку B( 2;7) параллельно прямой l : 5x y 9 0.
Решение. Изобразим данные задачи на рисунке. Дана точка B и прямая l . Проверим, лежит ли точка B на прямой l . Для этого необходимо подставить координаты точки B в уравнение прямой l . Если получится верное равенство,
то точка лежит на прямой, если не верное, то точка не лежит на прямой. При |
||
подстановке получаем: 5 2 7 9 0 |
или, |
после преобразований, 8 0. |
Равенство неверно, следовательно, точка |
B не |
лежит на прямой l . |
l
B
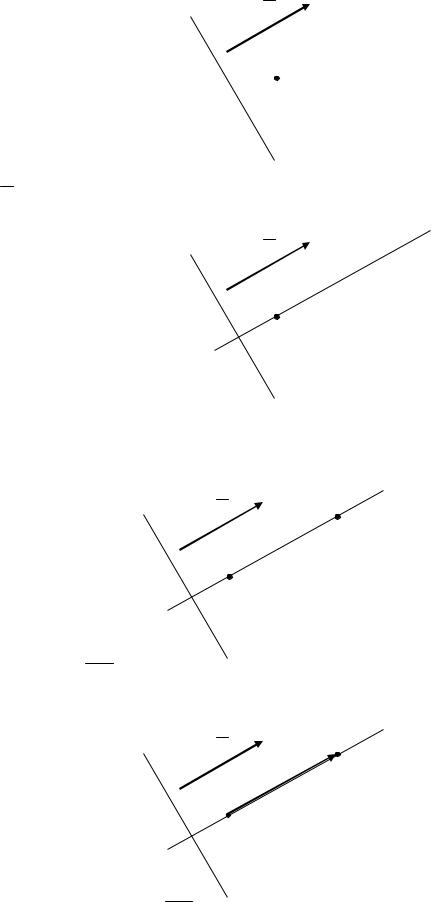
Прямая l задана общим уравнением, следовательно, можно указать координаты нормального вектора прямой, которыми являются коэффициенты при x и y в
уравнении прямой: N 5; 1 .
7
N
l
B
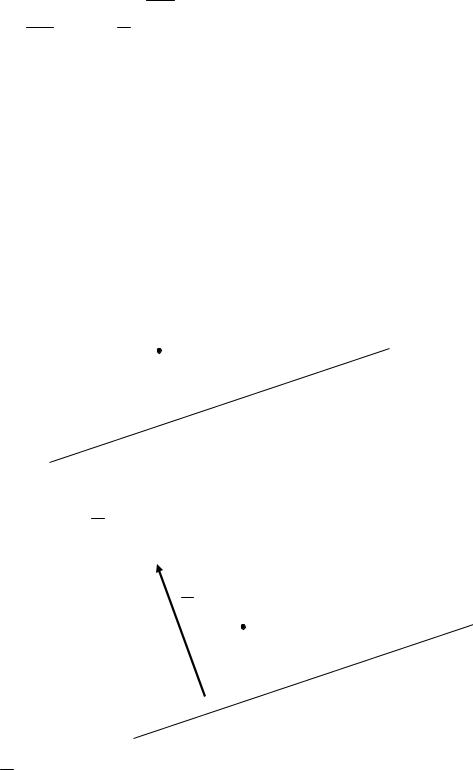
Проведем через точку B прямую перпендикулярно к прямой l (параллельно вектору N )
N
l
B
Записать уравнение прямой – значит связать некоторым равенством координаты произвольной точки прямой. Поэтому возьмем произвольную точку M x;y на искомой прямой:
N
M
l
B
Определим вектор BM :
N
M
l
B
Найдем координаты вектора BM :
8
BM x ( 2);y 7 x 2;y 7 .
Векторы BM и N коллинеарны, следовательно, их координаты пропорциональны. Запишем условие коллинеарности:
x 2 |
|
y 7 |
|
|
|
|
. |
5 |
1 |
||
Полученное равенство является каноническим уравнением искомой прямой.
Пример. Записать уравнение прямой, проходящей через точку C 3; 5 параллельно прямой l : 7x 4y 11 0.
Решение. Изобразим данные задачи на рисунке. Дана точка C и прямая l . Проверим, лежит ли точка C на прямой l . Для этого необходимо подставить координаты точки C в уравнение прямой l . Если получится верное равенство, то точка лежит на прямой, если не верное, то точка не лежит на прямой. При подстановке получаем: 7 3 4 5 11 0 или, после преобразований, 52 0. Равенство неверно, следовательно, точка C не лежит на прямой l .
C
l
Прямая l задана общим уравнением, следовательно, можно указать координаты нормального вектора прямой, которыми являются коэффициенты при x и y в
уравнении прямой: N 7; 4 .
N
C
l
Проведем через точку C прямую параллельно прямой l (перпендикулярно к вектору N )
9
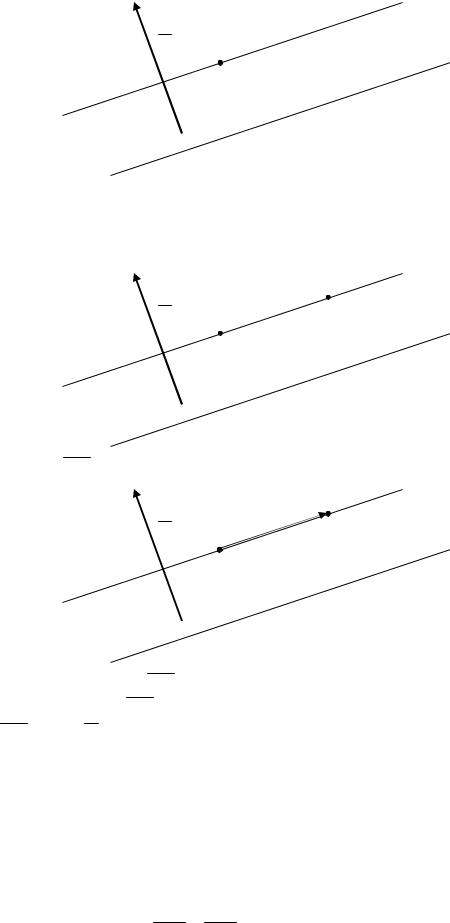
N
C
l
Записать уравнение прямой – значит связать некоторым равенством координаты произвольной точки прямой. Поэтому возьмем произвольную точку M x;y на искомой прямой:
N M
C
l
Определим вектор CM :
N M
C
l
Найдем координаты вектора CM :
CM x 3;y ( 5) x 3;y 5 .
Векторы CM и N перпендикулярны, следовательно, их скалярное произведение равно 0:
7 x 3 4 y 5 0.
После преобразований получаем:
7x 4y 41 0
Полученное уравнение является общим уравнением искомой прямой.
Пример. Записать уравнение прямой, проходящей через точку D 2;3
перпендикулярно к прямой l : x 31 y121.
10
