Математическая обработка результатов эксперимента

Статистикой называется функция результатов опыта, которая не зависит от неизвестных статистических характеристик.

Статистическая оценка θ٭ – это статистика, которая вычисляется на основании выборочной совокупности опытных данных и принимается за неизвестное истинное значение параметра θ. Статистическая оценка θ٭ параметра θ является случайной величиной и меняется от опыта к опыту. Запись θ٭ θ (или θ θ٭) читается следующим образом: θ٭ является статистической оценкой параметра θ. Нахождение статистических оценок называют точечным оцениванием.

Не каждая статистика может служить статистической оценкой. Во-первых, до вычисления статистических оценок опытные данные должны быть очищены от грубых, в частности систематических, ошибок путем приведенных выше процедур первичной обработ-

ки, способствующих репрезентативности выборочной совокупности. Во-вторых, с теоретической точки зрения статистическая оценка

должна вычисляться по формулам, которые обеспечивают состоятельность, несмещенность и эффективность этой оценки.

Если при неограниченном увеличении числа опытов (при n→∞ ) вероятность больших отклонений θ* от θ стремится к нулю, то такая оценка θ* называется состоятельной.

Если Мθ* = θ, т.е. если математическое ожидание Мθ* статистической оценки θ* равно θ, то оценка θ* называется неcмещенной.

Состоятельность и несмещенность – практически важные характеристики качества статистических оценок.

Для характеристики качества оценки используют также математическое ожидание квадрата отклонения θ* от θ, т.е. величину

δ = M │θ*− θ│2.

Статистическую оценку θ* с минимально возможным значением величины δ часто называют эффективной.

Приведем формулы для статистических оценок некоторых из приведенных выше (см. формулы (1.6), (1.7), (1.9)) числовых характеристик случайных величин.

41

Математическое ожидание MX случайной величины X, представленной выборочной совокупностью (x1, x2, …, xn) опытных значений, оценивается с помощью среднего выборочного значения xср по следующей формуле:

Доказано, что если математическое ожидание MX случайной величины конечно, то среднее выборочное значение xср, вычисляемое по формуле (4.1), является его несмещенной состоятельной оценкой [14].

Дисперсия и среднее квадратичное отклонение случайной величины X с (n−1) степенями свободы оцениваются по следующим формулам:

Отметим, что соответствующие выборочная (исправленная) дисперсия (SX)2 и выборочное (исправленное) среднее квадратичное отклонение SX, вычисляемые по формулам (4.2), являются состоятельными несмещенными оценками дисперсии DX и среднего квадратичного отклонения σX соответственно. В частности, M[(SX)2] = DX

и M(SX) = σX.

На основании выборочных совокупностей значений двух случайных величин X и Y приходится оценивать и коэффициент их корреляции

Пусть xi – опытные значения величины X, а xср – ее среднее выборочное значение (см. формулу (4.1)). Пусть yk – значения величины Y, а yср – ее среднее выборочное значение. Рассмотрим двумерную случайную величину (X,Y). Пусть (xi, yk) – это наблюдавшиеся пары значений, nik – их частота, а n – объем выборочной совокупности

42

двумерной случайной величины (X,Y), т.е. сумма частот nik наблюдавшихся пар (xi, yk).

Тогда статистическая оценка коэффициента rxy корреляции случайных величин X и Y выполняется с помощью выборочного коэффициента корреляции rвыб (X, Y) по следующей формуле [10]:

n

∑(nik xi yk −n xср yср)

Так как статистические оценки являются случайными величинами, то при принятии решений необходимо оценивать их статистическую значимость, которая зависит от объема и качественного состава выборочных совокупностей, а также от оценки важности принимаемого решения. Важность характеризуется уровнем значимости α, который устанавливает сам исследователь в зависимости от значимости последствий возможной ошибки при принятии решения. Напомним, что уровень значимости α – это вероятность ошибки первого рода, т.е. вероятность отвергнуть выдвинутую гипотезу, в то время как в действительности она верна. Обычно принимают одно из следующих значенийуровнязначимости: 0,10; 0,05 или 0,01.

Далее рассмотрены некоторые способы проверки значимости статистических оценок и выдвигаемых статистических гипотез. Более полный свод правил и процедур проверки разнообразных статистических гипотез можно найти вучебниках по статистике [10, 11].

4.2. Подбор закона распределения по экспериментальным данным

Во многих задачах теории принятия решений, связанных со статистической обработкой опытных данных, необходимо проверять гипотезы о характере и параметрах распределений вероятностей наблюдаемых значений. Например, расчеты теории надежности технических систем используют нормальный, показательный (экспоненциальный) законы распределения, закон Вейбулла – Гнеденко и другие.

43

С нормальным законом распределения вероятностей исследователям приходится сталкиваться наиболее часто, поэтому в этом разделе будет представлена процедура проверки гипотезы о нормальности распределения исследуемой совокупности опытных данных.

Кроме того, так как на основании опытных данных необходимо выполнять оценки числовых параметров распределения (в частности, математического ожидания MX и дисперсии DX), а никаких точных утверждений об этих величинах сделать нельзя, то можно лишь выдвигать о них различные гипотезы (предположения). Поэтому в этом разделе рассмотрены еще две задачи:

1)как проверить предположение о том, что исправленная выборочная дисперсия (SX)2, вычисляемая по формуле (4.2), и предполагаемая (гипотетическая) дисперсия DX генеральной совокупности отличаются статистически незначимо, т.е. при заданном уровне значимости их можно считать равными;

2)как проверить предположение о том, что средняя выборочная, вычисляемая по формуле (4.1), и предполагаемая (гипотетическая) генеральная средняя отличаются статистически незначимо, т.е. при заданном уровне значимости их можно считать равными.

Процедуры проверки гипотез зависят не только от их содержания, но и от вида нулевых и конкурирующих гипотез (см. учебники

[10, 16]).

4.2.1. Проверка гипотезы о нормальном распределении генеральной совокупности

Использование регрессионного анализа с целью прогноза также опирается на гипотезу о нормальности распределения исследуемой совокупности опытных данных, поэтому ниже процедуру подбора закона распределения по опытным данным представим именно на примере этого распределения.

Подбор вида любого из предполагаемых законов распределения рекомендуется начинать с построения гистограммы [10] опытных значений.

44

Для построения гистограммы сначала находят наименьшее xmin и наибольшее xmax из выборочных значений, а исходные данные xi

(i = 1, 2, …, n), т.е. промежуток [xmin, xmax], разбивают на ряд частичных интервалов. При разбиении исходного промежутка [xmin, xmax] на

ряд частичных часто применяется следующая формула для вычисления искомой длины частичных интервалов:

Число l таких частичных интервалов в дальнейшем может быть уменьшено, если в отдельные интервалы не попадает ни одного значения (или попадает слишком мало значений).

Гистограмма – ступенчатая фигура, состоящая из l прямоугольников с основаниями ∆х и различными высотами x j (j = 1,2,…, l), где

x j – это средние значения вариант, попавших в j-й интервал. График

функции f(x) – плотности распределения предполагаемого вероятностного закона, наложенный на гистограмму, наглядно позволяет судить о степени соответствия опытных данных и функции f(x) и выдвигать соответствующие гипотезы.

Если вид гистограммы указывает на то, что опытные данные могут соответствовать нормальному закону распределения (1.4), то выбор подходящей функции f(x) начинают со статистических оценок двух определяющих его характеристик a и σ – математического ожидания MX и среднего квадратичного отклонения σX соответственно. Статистические оценки параметров предполагаемого нормального распределения генеральной совокупности по опытным данным можно выполнить по формулам (4.1) и (4.2).

Для проверки согласованности распределения исследуемой случайной величины с нормальным распределением задается уровень значимости α и в качестве нулевой принимается гипотеза H0 о том, что генеральная совокупность распределена по нормальному закону.

Далее для проверки нулевой гипотезы при заданном уровне значимости α обычно используют критерии Пирсона χ2 или Колмогоро-

45

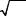
ва [14]. Используем критерий Пирсона χ2, так как он является более мощным по сравнению с критерием Колмогорова.

Расчетные значения критерия Пирсона вычисляются по следующей формуле:

где nj – число опытных данных, попавших в j-й интервал (j = 1, 2, …, l); n′j – теоретическое число данных, попавших в j-й интервал.

Доказано, если число п исходных данных неограниченно возрастает (n→∞), то закон распределения случайной величины (4.5), независимо от того, по какому закону распределена генеральная совокупность, стремится к закону распределения Пирсона χ2 с k степенями свободы, причем число k вычисляется следующим образом:

k = l −1−m,

где m – это число параметров предполагаемого распределения. Нормальное распределение определяется двумя параметрами a

и σ, т.е. в нашем случае m = 2, а число степеней свободы распределения Пирсона k = l −3.

Теоретическое значение величины n′j вычисляется в предположении о нормальности распределения по формуле

x j

где n – объем исходной выборочной совокупности.

Для нормально распределенных случайных величин теоретическое значение n′j вычисляется по следующей формуле:

46

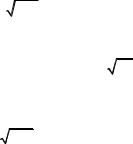
где a = MX, σ = DX , Φ(x) – стандартная функция Лапласа,

Стандартная функция Лапласа Φ(x) имеет нулевое математическое ожидание и среднее квадратичное отклонение σ, равное 1, т.е.

MX = 0 и σX = DX =1. Таблицу значений стандартной функции Лапласа Φ(x) можно найти во многих справочниках и учебниках по ста-

тистике [1, 5, 10, 11, 16].

После вычисления по формуле (4.5) расчетного значения χ2расч проверяется выполнение неравенства

где χкр2 – критическое значение критерия Пирсона, которое выбира-

ется из соответствующих статистических таблиц в зависимости от установленного в задаче уровня значимости α и числа k степеней свободы.

Если это неравенство выполнено, то при заданном уровне значимости α гипотеза о нормальности распределения исследуемой случайной величины, представленной своими выборочными значе-

ниями, принимается, в противном случае, т.е. если χ2расч ≥ χкр2 , гипотеза отвергается.

Сделаем ряд практических замечаний.

Для применения критерия Пирсона в качестве критерия согласия при проверке гипотезы о том или ином виде вероятностного распределения совокупности выборочных данных предварительно требуется выполнить два условия:

1. Объем выборки (число n опытных данных в совокупности) должен быть достаточно большим, так как теоретически критерий

47

справедлив при n→∞. Обычно требуют, чтобы исследуемая выборочная совокупность содержала не менее 150–200 значений.

2. Достаточно большим должен быть не только общий объем n выборочной совокупности, но и число ni выборочных данных, попавших в каждый из частичных интервалов разбиения, а именно: рекомендуется в среднем иметь по 5–10 % данных в каждом из интервалов. Если значение ni в отдельных интервалах мало (менее 1–2 %), и тем более если для некоторых интервалов ni = 0, то следует объединять такие интервалы.

В заключение отметим, что объем рассмотренных выше выборочных совокупностей явно недостаточен, поэтому проверять нормальность их распределения не имеет смысла.

4.2.2.Сравнение исправленной выборочной дисперсии

спредполагаемой генеральной дисперсией нормальной совокупности

Задача сравнения опытного значения дисперсии, зависящего от состава и объема выборочной совокупности, с предполагаемым (теоретическим) значением генеральной дисперсии возникает, например, в метрологии. При настройке или при техническом осмотре измерительной аппаратуры естественно считать, что теоретическое значение – это указанное в нормативно-технической документации значение цены деления прибора, точность которого подлежит проверке.

Если возникает предположение, что детали, изготовленные на устаревшем станке, не соответствуют нормативным требованиям и, следовательно, необходима замена или переналадка станка, то в качестве теоретического значения дисперсии генеральной совокупности выступает заданная точность изготовления детали, а выборочное значение дисперсии вычисляется по данным измерения изготовленных деталей.

В общем случае предполагается, что генеральная совокупность имеет нормальное распределение с неизвестными параметрами a = MX

и σ = DX . Но при этом, хотя генеральная дисперсия DX = σген2 нам

48

неизвестна, имеются основания предполагать, что она равна некоторому гипотетическому значению σ02 . Это предположение необходи-

мо проверять методами математической статистики. Проверка выполняется в несколько шагов.

На первом шаге задается уровень значимости α и выдвигается нулевая гипотеза H0, состоящая в том, что генеральная дисперсия

σген2 = DX равна ее предполагаемому значениюσ02 , т.е. нулевая гипотеза имеет вид

с k = n−1 степенями свободы. Это исправленное выборочное значение дисперсии (SX)2 является несмещенной оценкой генеральной дисперсии DX, т.е. M(S2X) = DX. Поэтому на третьем шаге нулевая гипотеза переписывается в следующем виде:

Гипотеза H0 означает, что при заданном уровне значимости α необходимо установить, является ли различие исправленной выборочной дисперсии (SX)2 и гипотетического значения генеральной

дисперсии σ02 незначимым.

В качестве критерия проверки нулевой гипотезы принимается случайная величина (статистика)

имеющая распределение Пирсона χ2 с k = n−1 степенями свободы.

Критическая область принятия гипотезы имеет различный вид в зависимости от вида конкурирующей гипотезы H1.

49

Первый случай. В качестве конкурирующей гипотезы H1 рассматривается предположение (4.12). Тогда критическая область является двухсторонней [10] и определяется двумя критическими точками: левой и правой.

Правая критическая точка ищется как критическое значение критерия Пирсона по формуле χправ2 .кр = χкр2 (α/2;k). Левая критическая точка ищется как критическое значение критерия Пирсона по формуле χ2лев.кр = χкр2 (1−α/2;k).

Если при этом опытное значение критерия χ2оп попадает в ин-

тервал ( χ2лев.кр ; χправ2 .кр ):

χ2лев.кр < χ2оп < χправ2 .кр ,

то при уровне значимости α нет оснований отвергать нулевую гипотезу, и мы считаем, что за искомое значение генеральной дисперсии DX можно принять найденное по формуле (4.2) значение (SХ)2.

Если же опытное значение критерия χ2оп не попадает в интервал

( χ2лев.кр ; χправ2 .кр ):

χ2оп < χ2лев.кр или χоп2 > χправ2 .кр ,

то нулевая гипотеза отвергается, и найденным значением исправленной выборочной дисперсии (SХ)2 нельзя пользоваться в качестве оценки генеральной дисперсии.

Второй случай. Сравнение исправленной выборочной дисперсии с предполагаемым значением дисперсии генеральной совокупности выполним на основе той же нулевой гипотезы H0 (4.10), но при конкурирующей гипотезе (4.13).

50