
Математическая обработка результатов эксперимента
..pdf1)типический отбор;
2)механический отбор;
3)серийный отбор.
При типическом отборе объекты извлекаются не из всей генеральной совокупности, а из некоторой ее «типической» части, к примеру, при исследовании мощностей двигателей машин изучению могут подлежать только машины отечественного производства. Типический отбор применяется в том случае, когда необходимо проанализировать результаты статистического исследования только в определенных (типических) группах генеральной совокупности.
При механическом отборе генеральную совокупность «механически» делят на группы в соответствии с тем, сколько объектов должно войти в выборку.
Механический отбор при проведении статистического анализа может быть применен тогда, когда требуется ограничить число объектов выборочной совокупности. В этом случае выбирают, например, каждый пятый, каждый десятый и т.д. объект и на основании полученной выборки проводят статистический анализ.
При серийном отборе объекты выбирают из генеральной совокупности не по одному, а сплошными сериями (например, первые
50объектов, вторые 100 и т.д.).
Влюбом случае объем извлекаемой выборки должен быть достаточно большим, чтобы на ее основе можно было делать статистически достоверные выводы.
2.3. Планирование эксперимента
Если у исследователя отсутствует возможность собрать достаточное количество известных опытных данных, то он должен прибегнуть к активным методам, т.е. спланировать и провести экспериментальные исследования самостоятельно.
Для этого он должен выполнить ряд условий, которые обеспечат достаточную точность и достоверность измерений, а также их полноту.
21

Точность и достоверность экспериментальных данных обеспечивается на основе использования соответствующих измерительных инструментов, удовлетворяющих необходимым метрологическим требованиям, а также многократного повторения измерений в заданной точке.
В случае нормального распределения значений измеряемой величины для оценки числа N повторений опытов, необходимого для достижения требуемой точности и достоверности измерения, можно пользоваться, например, следующей формулой [14, гл. 11.5]:
N > Nтреб = tα (DX )оп ,
∆2
где Nтреб – требуемое (минимальное) число повторений опыта; (DX)оп – опытное значение (статистическая оценка) дисперсии измеряемой величины X; tα – коэффициент, характеризующий вероятность α того, что модуль отклонения │MX–xср│ не превысит заданное значение ∆, т.е. вероятность выполнения неравенства
│MX – xср│< ∆,
где MX – искомое значение (математическое ожидание) измеряемой величины X; xср – ее среднее опытное значение. Например, при tα = 2 вероятность α = 0,95, а при tα = 3 вероятность α = 0,997 [10].
Проверка нормальности распределения опытных данных вокруг измеряемых значений в общем случае выполняется апостериори. В самых простых случаях, когда есть основания полагать, что все необходимые метрологические требования выполнены и данные рас-
пределены |
вокруг каждого из измеряемых |
значений нормально, |
||||
в каждой точке эксперимент, |
тем |
не менее, |
повторяют |
трижды, |
||
а в качестве |
результирующего |
в выборке |
фиксируется среднее из |
|||
трех полученных значений. |
|
|
|
|
|
|
Более |
подробное описание |
методик |
обеспечения |
точности |
||
и достоверности экспериментальных данных (в том числе процедур отбрасывания сомнительных данных) можно найти, например, в пособии В.И. Колесниченко [4, гл. 4–6].
22
При построении математической модели полнота опытных данных означает, что объем выборочной совокупности должен быть достаточно большим для того, чтобы на ее основе можно было оценить все параметры искомой модели. При планировании эксперимента вопрос о минимальном размере выборочной совокупности – это основной вопрос, который необходимо решить до его начала. Основы планирования эксперимента излагаются, например, в учебниках [9, 17]. Достаточность выборочных данных оценивается в ходе корреляционно-регрессионного анализа путем оценки адекватности построенной модели реальным данным, а также целям и задачам регрессионного анализа.
Контрольные вопросы
1.Что такое пассивный и активный эксперименты? Приведите примеры пассивного сбора опытных данных и примеры планирования эксперимента.
2.В каком случае выборку называют репрезентативной?
3.Как обеспечить репрезентативность выборочных данных? Перечислите основные принципы формирования выборочной совокупности.
4.Что означает требование системности выборочной совокуп-
ности?
5.Что означает требование полноты выборочной совокупности?
6.Как обеспечить корректность собираемых опытных данных?
7.Укажите некоторые методы сбора опытных данных. На какие две основные группы их можно разделить?
8.Что такое повторный и бесповторный отбор?
9.Приведите примеры, когда необходимо использовать типический (механический, серийный) отбор.
10.Приведите формулу для оценки числа N повторений опытов, необходимого для достижения требуемой точности измерения. Какое условие, обеспечивающее достоверность каждого из измеряемых значений, при этом должно быть выполнено?
23
3.МЕТОДЫ ПЕРВИЧНОЙ ОБРАБОТКИ ОПЫТНЫХ ДАННЫХ
Впроцессе сбора опытных данных возможны ошибки. Они бывают связаны с неточностью наблюдения за исследуемым процессом,
атакже с воздействием внешних и внутренних случайных факторов. Ошибки могут быть систематическими и случайными. Систематические ошибки могут возникать из-за сбоя в процедурах измерения или по техническим причинам. Случайные ошибки часто возникают в результате действия человеческого фактора, например стресса или усталости оператора. Поэтому для составления выборочной совокупности, пригодной для статистического анализа, необходимо исходную совокупность опытных данных подвергнуть процедурам первичной обработки.
Две главных процедуры первичной обработки опытных данных – это процедура исключения так называемых ложных данных и проверка данных на их независимость и случайность.
3.1.Процедура исключения ложных данных
Случайным путем ложные результаты проникают в исходную совокупность опытных данных из-за действия достаточно большого числа случайных причин, которые не удается заранее предусмотреть при проведении измерений или при сборе статистических сведений. Например, оператор, собиравший данные, сделал описку. Или при- бор-измеритель мог случайно подвергнуться постороннему воздействию именно в момент измерения.
Систематические ошибки приводят к ложным результатам измерений из-за действия фактора, который не был учтен, но постоянно влиял на результаты. Например, измерения регулярно проводились в одну и ту же рабочую смену, хотя опытные данные затем распространялись на все смены. Прибор-измеритель мог стоять утром на нагретой солнечной стороне, а вечером – в тени, причем влиянием
24
этого обстоятельства на значения измеряемой величины пренебрегли, хотя оно могло оказаться значимым.
Наконец, нельзя исключать случай, когда ошибки в статистические данные вносятся злонамеренно, например, с целью искажения или сокрытия истинного положения вещей.
Процедура исключения ложных данных позволяет выявить такие данные в статистической совокупности с большой степенью вероятности.
К источникам ложных данных относятся:
–грубые (недостаточно точные) измерения;
–нарушение условий эксперимента;
–использование неисправного оборудования;
–ошибки при обработке информации и др.
Наличие ложных данных приводит к необоснованным выводам, поэтому ложные данные должны быть исключены из выборочной совокупности в процессе первичной обработки опытных данных.
Суть методики исключения ложных данных состоит в проверке однородности собранной совокупности. Если некоторые элементы совокупности опытных данных заметно выбиваются из общей массы, то, скорее всего, они являются ложными и их необходимо исключить из выборочной совокупности. Процедура исключения ложных данных состоит в проверке определенных статистических гипотез и выполняется при заданном уровне значимости α (т.е. с определенной вероятностью совершить ошибку, исключив данные, которые на самом деле не были ложными).
Теоретические положения, связанные с основными понятиями и процедурами проверки статистических гипотез, можно найти в учебниках по статистике [1, 10, 11].
Изложим процедуру исключения ложных данных поэтапно. Пусть имеется числовая случайная величина X, принимающая
множество различных значений {x: x X}.
Первый этап. Имеющиеся значения совокупности опытных значений случайной величины X располагаются в порядке их неубыва-
25
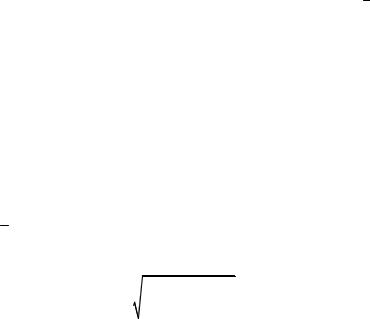
ния: x(1) ≤ x(2) ≤ … ≤ x(m), и определяются крайние элементы представленной совокупности:
x(1) = xmin, x(n) = xmax.
Если значения xmin и xmax резко отличаются от остальных значений выборки, то появляется необходимость в статистической проверке двух конкурирующих гипотез (предположений):
–гипотеза Н1: все исходные данные получены при неизменных условиях, и выборку можно считать однородной;
–гипотеза Н2: значение одного из результатов xmin или xmax (или обоих вместе) получено при существенно изменившихся условиях, и эти значения необходимо исключить из выборочной совокупности.
Второй этап. Вычисляются следующие расчетные (опытные)
значения τminpасч , τmaxpасч отклонений крайних значений случайной вели-
чины xmin , xmax от ее среднего значения x с учетом разброса S значений случайной величины Х в выборке по формулам:
τpminасч |
= |
xmin − x |
, τpmaxасч = |
xmax − x |
|
. |
(3.1) |
|||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
S |
S |
|||||||||||
|
|
|
|
|
||||||||
Среднее значение опытных данных x вычисляется по исходной совокупности объемом m по следующей формуле:
|
1 |
m |
|
|
x =x(m) = |
∑xi . |
(3.2) |
||
m |
||||
|
i=1 |
|
||
|
|
|
Также по исходной совокупности опытных данных вычисляется
величина S , характеризующая разброс опытных значений величины X вокруг среднего x :
|
|
|
|
1 |
m |
|
|||
S |
= |
S |
(m) = |
∑(xi − |
x |
)2 . |
(3.3) |
||
m−1 |
|||||||||
|
|
|
|
i=1 |
|
||||
|
|
|
|
|
|
||||
26

Третий этап. Расчетные значения τрасч относительного отклонения τ(α;m) сравниваются с его критическими (теоретическими) значениями τкр(α;m), которые можно найти в таблицах распределения соответствующей статистики при заданном объеме m выборочной совокупности и заданном значении уровня значимости α.
При небольших выборках (m ≤ 25) для исключения ложных данных рекомендуется использовать таблицу квантилей распределения максимального относительного отклонения τ(α;m). Некоторые значения квантилей максимального относительного отклонения τкр(α;т) для двух различных значений уровня значимости α приведены в табл. 3.1.
Таблица 3 . 1
Квантили максимального относительного отклонения
α, |
|
|
|
Объем выборочной совокупности т |
|
|
|
|||||||
% |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
1 |
2,66 |
2,71 |
2,76 |
2,8 |
2,84 |
2,87 |
2,9 |
2,93 |
2,96 |
2,98 |
3,01 |
3,03 |
3,05 |
3,07 |
5 |
2,39 |
2,43 |
2,46 |
2,49 |
2,52 |
2,55 |
2,58 |
2,60 |
2,62 |
2,64 |
2,66 |
2,68 |
2,70 |
2,72 |
Более полные таблицы статистики τ(α;m) содержатся в справочниках и учебниках по математической статистике [1, 11].
Сравниваются расчетное и критическое значения по следующей формуле:
τрасч ≤ τкр (α; m). |
(3.4) |
Если неравенство (3.4) выполнено, то проверяемое |
значение |
(xmin или xmax) не считают ложным и оставляют в выборке. В противном случае его удаляют из исходной совокупности. После исключе-
ния каждого из ложных значений характеристики x и S необходимо пересчитывать. Значения уровня значимости α выбирает исследователь в зависимости от рассматриваемой задачи и цели исследования. Обычно в технических расчетах принимают значение вероятности
α = 0,05 или α = 0,01.
27
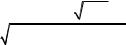
При больших объемах опытных данных (m ≥ 25) для исключения ложных результатов эксперимента рекомендуется использовать t-распределение Стьюдента.
Критерием проверки конкурирующих гипотез Н1 и Н2 в этом случае служат следующие неравенства:
τрасч ≤ τкр (0,05; m), |
(3.5) |
τкр(0,05; т) < τрасч ≤ τкр (0,01; m), |
(3.6) |
τрасч > τкр (0,01; m). |
(3.7) |
Расчетное значение критерия τрасч вычисляют по одной из формул (3.1) (для значений xmin или xmax соответственно), а критические значения критерия τкр(α;m) – по следующей формуле:
τкр(α;m) = |
t(α,m−2) m−1 |
. |
(3.8) |
|
(m−2)+t 2(α;m−2) |
||||
|
|
|
Здесь t(α;m−2) – это критические точки распределения Стьюдента при заданном значении уровня значимости α и заданном объеме ν = m−2 выборочной совокупности. Критические точки распределения Стьюдента t(α;ν) также следует искать в справочниках или учебниках по математической статистике.
В качестве примера некоторые значения распределения Стьюдента в случае односторонней критической области для двух различных значений уровня значимости α приведены в табл. 3.2.
Таблица 3 . 2
Критические точки распределения Стьюдента t(α;ν) для односторонней критической области
α |
|
|
|
Объем ν выборочной совокупности |
|
|
|
||||||
|
26 |
27 |
28 |
|
29 |
30 |
32 |
34 |
36 |
|
40 |
44 |
50 |
0,01 |
2,4786 |
2,4727 |
2,4621 |
2,4620 |
2,4573 |
2,4487 |
2,4411 |
2,4620 |
2,4233 |
2,4141 |
2,4033 |
||
0,05 |
1,7056 |
1,7033 |
1,7011 |
1,6991 |
1,6973 |
1,6939 |
1,6909 |
1,6883 |
1,6839 |
1,6802 |
1,6759 |
||
28 |
|
|
|
|
|
|
|
|
|
|
|
|
|

|
|
|
|
|
|
|
|
Окончание |
табл. 3 . 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
α |
|
|
|
Объем ν выборочной совокупности |
|
|
|
|
||||||
60 |
70 |
90 |
|
100 |
120 |
150 |
200 |
250 |
|
300 |
|
400 |
5000 |
|
0,01 |
2,3901 |
2,3808 |
2,3685 |
2,3642 |
2,3578 |
2,3515 |
2,3451 |
2,3414 |
2,3388 |
2,3357 |
2,3338 |
|||
0,05 |
1,6706 |
1,6669 |
1,6620 |
1,6602 |
1,6577 |
1,6551 |
1,6525 |
1,6510 |
1,6499 |
1,6487 |
1,6479 |
|||
При выполнении неравенства (3.5) рассматриваемые опытные значения никогда не исключают из исходной совокупности. При выполнении неравенства (3.6) рассматриваемые значения можно исключить, если для этого есть какие-либо дополнительные аргументы. При выполнении неравенства (3.7) рассматриваемые значения всегда исключаются как ложные. Процедуру исключения необходимо повторять вплоть до выполнения неравенств (3.5) и (3.6), при этом ка-
ждый раз снова пересчитывая характеристики x , S .
Рассмотрим процедуру исключения ложных данных на следующем примере.
Пример 3.1. Пусть имеются две совокупности значений случайных величин X и Y (табл. 3.3), полученных в результате эксперимента, каждая из которых имеет объем m = m1 = m2 = 30.
Таблица 3 . 3
Опытные значения величин X и Y
т |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|||||
X |
3 |
8 |
11 |
15 |
15 |
3 |
10 |
5 |
4 |
14 |
13 |
1 |
9 |
0 |
5 |
|||||
Y |
7 |
9 |
10 |
14 |
15 |
5 |
12 |
7 |
6 |
15 |
14 |
3 |
10 |
0 |
6 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончание табл. 3 . 3 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
т |
|
16 |
|
17 |
|
18 |
|
19 |
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
X |
|
3 |
|
6 |
|
15 |
|
2 |
|
6 |
9 |
9 |
8 |
0 |
11 |
13 |
2 |
5 |
6 |
4 |
Y |
|
4 |
|
8 |
|
15 |
|
3 |
|
7 |
8 |
15 |
8 |
0 |
9 |
10 |
5 |
7 |
10 |
4 |
Так как объем данных достаточно велик (m = m1 = m2 = 30 > 25), то можно воспользоваться таблицей распределения Стьюдента.
Сначала выполним процедуру исключения ложных данных из представленной совокупности опытных значений случайной величины X:
29
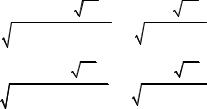
1. Упорядочим значения величины X по неубыванию, т.е. составим вариационный ряд из значений величины X:
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
X |
0 |
0 |
1 |
2 |
2 |
3 |
3 |
3 |
4 |
4 |
5 |
5 |
5 |
6 |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
№ |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
X |
6 |
8 |
8 |
9 |
9 |
9 |
10 |
11 |
11 |
13 |
13 |
14 |
15 |
15 |
15 |
Найдем минимальное и максимальное значения случайной величины X:
xmin = 0; xmax = 15.
2. Вычислим опытные значения τminpасч и τmaxpасч для случайной величины X. Для этого вычислим среднее значение x случайной вели-
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
чины X и оценку S |
ее среднего квадратичного отклонения (разбро- |
|||||||||||||||||
са). Получим, что x |
= 7,2; |
|
= 4,6. |
|
|
|
||||||||||||
S |
|
|
|
|||||||||||||||
Тогда согласно формулам (3.1) получим: |
||||||||||||||||||
|
|
| xmin − |
|
|
| |
|
|0−7,2| |
|
||||||||||
τpminасч = |
x |
= |
≈1,565; |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
4,6 |
|
|||||||
|
|
|
|
S |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
| xmax − |
|
| |
|
|15−7,2| |
|
||||||||||||
τpmaxасч = |
x |
= |
≈1,696. |
|||||||||||||||
|
|
|
|
|
|
|
4,6 |
|
||||||||||
|
|
|
S |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
3. Проверим выполнение неравенств (3.5) – (3.7).
Для этого найдем значения величин τкр(0,05;m) и τкр(0,01;m)
при m = 30:
τкр(0,05; 30) = |
t(0,05;28) 29 |
= |
|
1,701 29 |
= 1,649; |
||||
28+[t(0,05;28)]2 |
28+1,7012 |
||||||||
|
|
|
|
|
|
||||
τкр(0,01; 30) = |
|
t(0,01;28) 29 |
|
= |
|
2,477 29 |
|
= 2,283. |
|
|
28+[t(0,01;28)]2 |
|
28+2,4772 |
|
|||||
30
