Кристаллография

а б Рис. 4. Типы пустот в плотнейших упаковках: а – тетраэдрическая;

б – октаэдрическая

Размеры тетраэдрической и октаэдрической пустот принято характеризовать радиусами сфер, которые можно вписать в эти пустоты: радиус сферы, вписанной в тетраэдрическую пустоту, rтетр = 0,225Rш, а радиус сферы, вписанной в октаэдрическую пустоту, rокт = 0,414Rш где Rш – радиус шара плотнейшей упаковки. Объем шариков радиусами rокт и rтетр, заполняющих без промежутков пустоты плотнейших упаковок, очень невелик: шарики, находящиеся во всех октаэдрических пустотах, занимают 5,255 %, а находящиеся во всех тетраэдрических пустотах – лишь 1,687 % пространства, приходящегося на упаковку. Гексагональная и кубическая плотнейшие упаковки различаются, следовательно, не числом или размерами пустот,

алишь их взаимным расположением.

Вгексагональной решетке на каждый атом приходится две тетраэдрические и одна октаэдрическая пустоты. Тетраэдрическая пустота находится между тремя атомами базисной плоскости и одним атомом внутри объема гексагональной призмы, а октаэдрическая – между тремя атомами базисной плоскости и тремя атомами внутри объема гексагональной призмы.

Вгранецентрированной кубической решетке тетраэдрические пустоты находятся на пространственных диагоналях куба на расстоянии ¼ диагонали от вершины элементарной ячейки. Октаэдрические пустоты расположены посредине ребер, а одна пустота находится в центре объема элементарной ячейки.

61

Объемноцентрированная кубическая (ОЦК) решетка не относится к предельно плотной упаковке, ее коэффициент компактности равен 68 %. Октаэдрические пустоты расположены в середине ребер и в центрах граней элементарной ячейки. В октаэдрическую пустоту можно вписать шар с радиусом всего 0,15Rш. В тетраэдрическую пустоту можно вписать шар с радиусом 0,291Rш.

Если кристаллическая решетка какого-либо соединения построена по принципу плотнейшей упаковки и материальные частицы, составляющие ее, можно аппроксимировать сферами разных радиусов, то роль шаров плотнейшей упаковки играют самые крупные частицы, а пустоты между ними занимают частицы более мелкие.

Например, в кристаллах двойных соединений с ионным взаимодействием анионы, имеющие, как правило, гораздо большие размеры, чем катионы, образуют плотнейшие упаковки, а катионы располагаются втетраэдрических иоктаэдрических пустотах этихупаковок.

Как показал выдающийся российский кристаллограф Н.В. Белов, посредством плотнейших упаковок шаров-анионов, пустоты между которыми заполнены шарами-катионами, с исчерпывающей полнотой можно описать большинство структур известных минералов сложного состава.

Несмотря на то что наиболее распространенными являются всего лишь две плотнейшие упаковки – гексагональная и кубическая, существует чрезвычайно большое количество плотноупакованных кристаллических структур. Это обусловлено не столько слойностью плотнейшей упаковки анионов, сколько типом и долей заполненных катионами пустот и законом их заполнения в тех случаях, когда часть пустот оказывается свободной.

Зная тип и долю заполненных пустот плотнейшей упаковки, можно определить стехиометрическую формулу любого вещества. Например, в структуре одной из шпинелей атомы кислорода образуют трехслойную плотнейшую упаковку, в которой половину октаэдрических пустот занимают атомы алюминия и восьмую часть тетраэдрических пустот – атомы магния. Поскольку в плотнейших упаковках на N атомов приходится N октаэдрических и 2N тетраэдрических пустот, то стехиометрическая формула этой шпинели ON

AN·1/2Mg2N·1/8 → MgAl2O4 → MgO·Al2O3.

62

Порядок выполнения работы

1.Ознакомиться с теоретической частью лабораторной работы.

2.Составить полную кристаллографическую характеристику следующих кристаллографических ячеек: объемноцентрированной кубической, гранецентрированной кубической, гексагональной плотноупакованной, примитивной кубической. Для каждой кристаллической ячейки определить число атомов на ячейку и координационное число, координационный многогранник, число формульных единиц; определить и записать базис; рассчитать коэффициент компактности; определить тип плотнейшей упаковки, число октаэдрических и тетраэдрических пустот на атом.

При описании необходимо пользоваться моделями решеток.

Содержание отчета

1.Название и цель лабораторной работы.

2.Краткие теоретические сведения.

3.Кристаллографическая характеристика кристаллографических ячеек.

Контрольные вопросы

1.Что называется ячейкой?

2.Как выделить в структуре элементарную ячейку Бравэ?

3.Что называется базисом ячейки?

4.Как определяются координаты узлов базиса?

5.Как подсчитывается количество атомов в ячейке?

6.Что такое координационное число ячейки?

7.Какая плотность упаковки является максимальной?

8.Сколько шаров образуют тетраэдрическую и октаэдрическую пустоты?

9.Почему у разных веществ различное расстояние между атомами в ячейке?

63

Лабораторная работа № 5 Определение элементов симметрии

и пространственных групп симметрии на моделях кристаллических структур

Цель работы – приобретение навыков определения винтовых осей симметрии, плоскостей скользящего отражения и пространственных групп симметрии на моделях кристаллических структур кубической и гексагональной сингоний.

Основные теоретические положения

Элементы симметрии кристаллических структур

Основное свойство кристаллической структуры и характеризующей ее пространственной решетки – бесконечная периодичность: любые два узла решетки можно совместить друг с другом при помощи трансляции.

Все элементы симметрии кристаллических многогранников встречаются также у кристаллических структур. В кристаллических структурах, как и в кристаллических многогранниках, действие поворотных осей симметрии приводит к самосовмещению при полном повороте вокруг оси симметрии. Действие инверсионных осей симметрии 3,4 и 6 в кристаллических структурах тоже аналогично действию этих осей в кристаллических многогранниках – оно состоит в повороте вокруг оси на соответствующий элементарный угол и мысленном отражении в центральной точке, лежащей на этой оси. Также у кристаллических структур дополнительно появляется новый элемент симметрии – ось трансляции. Сочетание трансляции с плоскостями и осями симметрии дает два новых элемента симметрии – плоскости скользящего отражения и винтовые оси симметрии.

Плоскость скользящего отражения – это мысленно проводи-

мая в структуре плоскость, отражаясь в которой кристаллическая решетка приходит в самосовмещение лишь после дополнительного переноса вдоль плоскости на определенную долю соответствующих

64

трансляций. На рис. 1 показаны условные обозначения и результаты действия на заданные точки плоскости симметрии т и пяти различных плоскостей скользящего отражения.

Рис. 1. Действие плоскостей симметрии m и плоскостей скользящего отражения a, b, c, n, d

Плоскости симметрии а, b и с сходны по своему действию, которое заключается в отражении и последующем переносе (скольжении) параллельно соответствующей координатной оси на половину трансляции вдоль этой оси. Иначе говоря, плоскости симметрии а, b и с параллельны осям X, Y и Z и обладают переносами а/2, b/2, с/2, где а, b и с – осевые трансляции.

В элементарных ячейках кристаллических структур плоскости симметрии а, b и с обычно располагаются параллельно граням ячейки, а иногда – параллельно диагоналям граней.

Действие плоскости скользящего отражения п, или клиноплоскости, состоит в отражении с последующим переносом на расстояния, равные половинам трансляций по двум направлениям, параллельным плоскости п. Когда плоскость симметрии п располагается параллельно какой-либо паре координатных осей (т.е. параллельно какой-либо грани элементарной ячейки), возможные переносы составляют (а+b)/2, (а+с)/2 или(b+с)/2.

Если же плоскость симметрии п располагается параллельно диагонали грани элементарной ячейки, то в качестве одного из переносов берется половина трансляции вдоль этой диагонали.

Действие плоскости симметрии d и ее расположение относительно граней элементарной ячейки аналогичны действию и расположению плоскости симметрии п, но переносы в случае плоскости d вдвое меньше: например, (а+b)/4, (а+с)/4 или (b+с)/4.

65

Необходимо помнить, что плоскости п и d встречаются соответственно в объемноцентрированных и гранецентрированных решетках Бравэ.

Плоскости скользящего отражения изображаются различными пунктирами, а на плоскости d еще ставятся значки, указывающие направление скольжения.

Винтовой осью симметрии называется ось, при повороте вокруг которой на соответствующий элементарный угол самосовмещение достигается только после дополнительного переноса вдоль оси на некоторую часть соответствующей трансляции. Наименьший перенос, возможный для винтовой оси симметрии n-го порядка, равен величине трансляции t в направлении оси, деленной на порядок оси: t/п. Помимо осей с наименьшим переносом возможны винтовые оси с переносом, кратным наименьшему. Винтовые оси симметрии в кристаллических структурах, как и поворотные и инверсионные оси симметрии, могут быть только второго, третьего, четвертого и шестого порядков. При этом различают винтовые оси правые и левые: принимается, что для правой винтовой оси поворот вокруг нее происходит по часовой стрелке, а для левой – против часовой стрелки, если смотреть по направлению переноса.

Винтовые оси симметрии, встречающиеся в кристаллических структурах, обозначаются международными символами, показывающими порядок оси, с числовыми индексами внизу: 21, 31, 32, 41, 42, 43, 61, 62, 63, 64, 65. В этих обозначениях частное от деления индекса на символ дает величину переноса вдоль данной оси по отношению к трансляции структуры в направлении, параллельном этой оси.

Например, ось 21 (рис. 2) означает поворот на 180° с последующим переносом вдоль нее на t/2. При этом двойная винтовая ось является одновременно и правой и левой, так как поворот вокруг нее на 180° по часовой стрелке или против нее приводит к одинаковому результату.

66

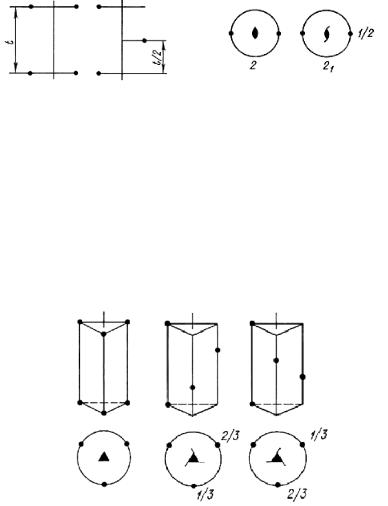
а б Рис. 2. Действиеповоротнойосисимметрии2 ивинтовойосисимметрии21:

а– расположенныхпараллельноплоскости чертежа; б– расположенных перпендикулярно плоскостичертежа

От выбора направления поворота вокруг оси не зависит также и действие осей 42 и 63. Поэтому оси 21, 42 и 63 называются нейтральными (оси 42 и 63 являются одновременно двойной и тройной поворотными осями симметрии, соответственно).

Ось 31 означает поворот на 120° по часовой стрелке с переносом вдоль нее на t/3, а ось 32 – такой же поворот, но с переносом на 2/3 t (рис. 3). Очевидно, что действие оси 31 правой тождественно действию оси 32 левой и оси 32 правой – оси 31 левой.

а

б

Рис. 3. Действие поворотной оси симметрии 3 и винтовых осей симметрии 31 и 32: а – расположенных параллельно плоскости чертежа; б – расположенных перпендикулярно плоскости чертежа

Для четвертой винтовой оси возможны трансляции t/4, 2t/4, 3t/4. Правая ось 41, эквивалентна левой 42 так же, как левая правой. Ось 42 является одновременно простой осью 2 (рис. 4).

67

Рис. 4. Действие поворотной оси симметрии 4 и винтовых осей симметрии 41, 42 и 43

Действию винтовой оси симметрии должны подчиняться все частицы кристаллической структуры, в том числе и находящиеся на самой оси. Поэтому, чтобы убедиться в существовании в структуре какой-либо винтовой оси симметрии, следует проверить ее действие на возможно большем числе частиц.

Если вершина элементарной ячейки совмещена с центром симметрии, ребро ячейки – с осью симметрии, а грань ячейки – с плоскостью симметрии, то и в других вершинах, ребрах и гранях этой ячейки окажутся те же элементы симметрии. Однако наличие в кристаллической решетке трансляций приводит к тому, что аналогичные находящимся в вершинах, на ребрах и на гранях элементы симметрии окажутся расположенными и внутри элементарной ячейки.

Пространственные группы симметрии и правильные системы точек

Бесконечные кристаллические решетки помимо элементов симметрии, свойственных конечным кристаллическим многогранникам, могут обладать еще и такими вышеперечисленными элемен-

68

тами симметрии, как трансляции, плоскости скользящего отражения и винтовые оси симметрии.

Подобно тому, как классом симметрии кристаллического многогранника называется совокупность всех его элементов симметрии, совокупность всех элементов симметрии кристаллической решетки называется пространственной группой симметрии. Поскольку раз-

личных элементов симметрии у кристаллических решеток значительно больше, чем у кристаллических многогранников, то и пространственных групп должно быть больше, чем классов симметрии.

В 1890 г. один из основоположников современной структурной кристаллографии Е.С. Федоров опубликовал первый теоретический вывод всех возможных сочетаний элементов симметрии кристаллических решеток. Оказалось, что таких сочетаний, т.е. пространст-

венных групп, может быть только 230 (2 в триклинной сингонии, 13 – в моноклинной, 59 – в ромбической, 25 – в тригональной, 68 – в тетрагональной, 27 – в гексагональной и 36 – в кубической).

Международный символ пространственной группы симметрии

состоит из большой латинской буквы (Р, I, А, В, С или F), обозначающей решетку Бравэ, и одного, двух или трех числовых либо буквенных символов, характеризующих симметрию главных направлений. Эта часть международного символа пространственной группы составляется по тем же правилам, что и международный символ соответствующего класса симметрии, с той лишь разницей, что в символе пространственной группы некоторые или все элементы симметрии символа класса симметрии могут быть заменены сходственными элементами симметрии (таблица).

69

Правила записи символа пространственной группы

Например, при описании пространственных групп симметрии, относящихся к кубической сингонии, на первом месте в символе ставятся буквы Р, I или F, обозначающие типы возможных решеток Бравэ. Буквы или цифры, стоящие на втором месте, определяют плоскости или оси симметрии, параллельные трансляциям в координатных направлениях <001>, т.е. проходящие параллельно ребрам элементарной ячейки. На третьем месте в символах пространственных групп симметрии кубической сингонии всегда стоит цифра 3, обозначающая оси третьего порядка, являющиеся направлениями типа <111>. Буквы или цифры, стоящие на четвертом месте, указывают, какие элементы симметрии параллельны направлениям <110>, т.е. проходят параллельно диагоналям граней. Если же элементы симметрии в этих направлениях отсутствуют, то цифра 3 является последней.

Когда в кристаллической структуре кубической сингонии в ка- ком-либо из главных направлений (<100>, <111> и <110>) одновременно располагаются и плоскости, и оси симметрии, в символ про-

70