
303208
.pdf
2885
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ЛИПЕЦКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»
Кафедра информатики
ЧИСЛЕННЫЕ МЕТОДЫ
Методические указания к выполнению лабораторных работ
Составитель С.А. Суслова
Липецк Липецкий государственный технический университет
2012
УДК 519.6(07) C904
Рецензент – Н.П. Гвозденко, канд. техн. наук, доц.
Суслова, С.А.
Численные методы [Текст]: методические указания к выполнению лабораторных работ / С.А. Суслова. – Липецк: Изд-во ЛГТУ, 2012. –
33 с.
В методических указаниях приведены краткие сведения и формулы по темам «Приближенное вычисление определенных интегралов», «Решение нелинейных уравнений», «Решение системы линейных уравнений», «Решение систем обыкновенных дифференциальных уравнений». Рассматриваются алгоритмы реализации численных методов.
Предназначены для студентов технических специальностей.
Табл. 4 . Ил. 14.
ФГБОУ ВПО «Липецкий государственный технический университет», 2012
2
Содержание
Лабораторная работа №1
Приближенное вычисление определенных интегралов (метод прямоугольников, метод трапеций, метод Симпсона)
1. |
Методические указания к выполнению работы |
..........................................4 |
2. |
Задание ........................................................................................................ |
8 |
3. |
Порядок выполнения лабораторной работы ............................................... |
8 |
4. |
Контрольные вопросы ................................................................................. |
9 |
5. |
Варианты заданий ..................................................................................... |
10 |
Лабораторная работа №2
Решение нелинейного алгебраического уравнения (метод деления отрезка пополам, метод касательных, метод хорд)
1. |
Методические указания к выполнению работы ........................................ |
11 |
2. |
Задание ...................................................................................................... |
14 |
3. |
Порядок выполнения лабораторной работы ............................................. |
16 |
4. |
Контрольные вопросы ............................................................................... |
17 |
5. |
Варианты заданий ..................................................................................... |
19 |
Лабораторная работа №3
Решение системы линейных алгебраических уравнений (метод Гаусса, метод итераций)
1. |
Методические указания к выполнению работы ................................................................... |
20 |
2. |
Задание ...................................................................................................... |
24 |
3. |
Порядок выполнения лабораторной работы ............................................. |
24 |
4. |
Контрольные вопросы ............................................................................... |
26 |
5. |
Варианты заданий ..................................................................................... |
27 |
Лабораторная работа №4
Решение систем обыкновенных дифференциальных уравнений методом Рунге-Кутта
1. |
Методические указания к выполнению работы .................................... |
28 |
2. |
Задание .................................................................................................. |
29 |
3. |
Порядок выполнения лабораторной работы .......................................... |
29 |
4. |
Контрольные вопросы ........................................................................... |
30 |
5. |
Варианты заданий .................................................................................. |
10 |
Библиографический список …………………………………………………….32
3
Лабораторная работа №1 Приближенное вычисление определенных интегралов
1. Методические указания к выполнению работы
Численное интегрирование основано на геометрическом смысле опреде-
ленного интеграла, который заключается в том, что значение
= ∫ ( )
равно площади фигуры, ограниченной осью абсцисс, прямыми = , = и
кривой подынтегральной функции. Эту фигуру (криволинейную трапецию) разбивают на ряд элементарных фигур с легко вычисляемыми площадями, суммирование которых дает искомое значение интеграла.
Метод прямоугольников
Разбиение интервала интегрирования [; ] на n частей приводит к воз-
можности рассмотрения площадей криволинейных трапеций на каждом небольшом отрезке , + .
Учитывая малую величину шага разбиения = −, площадь такой фи-
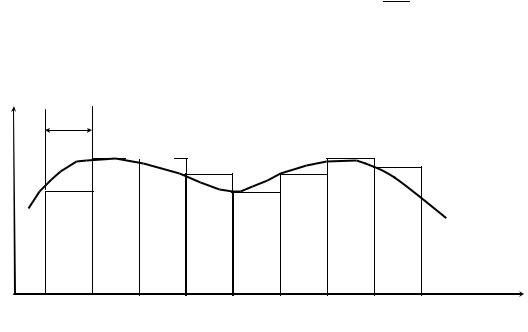
гуры можно считать приближенно равной площади прямоугольника со сторонами и h (рис.1).
Y
|
|
Y1 |
Y2 |
|
|
Yi+1 |
Yn |
|
|
|
|
|
|
Yi |
|
||
|
|
|
|
|
|
|
||
|
Y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Y=F(x) |
0 |
x0=a |
x1 |
x2 |
…. |
xi |
xi+1… |
xn=b |
X |
Рис.1. Графическая интерпретация метода прямоугольников
4
Суммирование значений таких площадей ( |
|
= |
∙ ) позволяет полу- |
|
|
|
|
|
|
чить формулу «левых» прямоугольников |
|
|
|
|
|
− |
|
|
|
∫ ( ) ≈ ∑ ( ) . |
|
|
|
|
|
= |
|
|
|
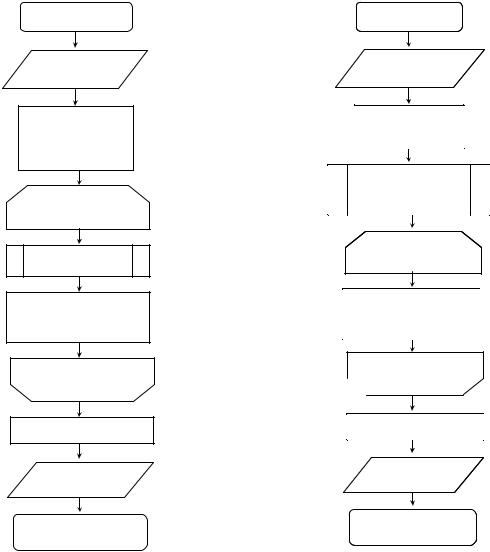
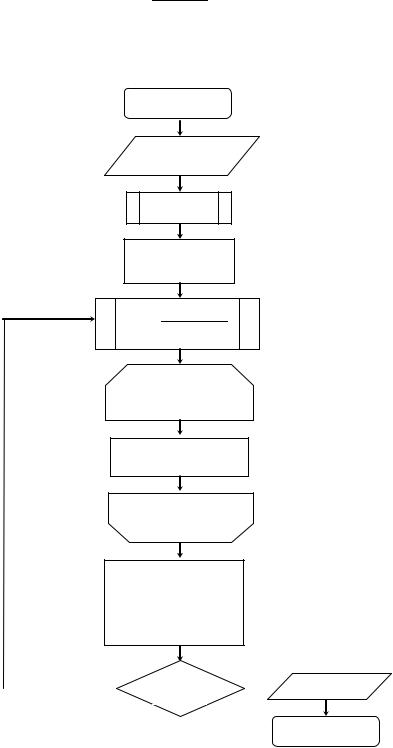
Блок-схема метода прямоугольников представлена на рис.2.
Начало
Ввод a,b,n
h=(b-a)/n S=0
X=a
j=1, n
F(x)
S=S+F(x) x=x+h
Конец цикла j
I=S*h
Вывод I
Конец
Рис.2. Блок-схема алгоритма метода прямоугольников
Начало
Ввод a, b, n
H=(b-a)/n
X=a
= ( )+ ( ) 2
j=2, n
x=x+h S=S+F(x)
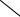 Конец цикла j
Конец цикла j
I=S*h
Вывод I
Конец
Рис.3- Блок-схема алгоритма Рис.3. Блок-схема алгоритма метода трапеций
метода трапеций
5

Метод трапеций
Замена интеграла
|
|
|
|
|
|
|
|
|
+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= ∫ |
( ) |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
на |
каждом |
элементарном участке |
площадью |
трапеции |
с основаниями |
|||||||||||
|
( |
), |
|
( |
+ |
) |
и высотой |
h |
( |
|
= ( |
+ |
)/ ) |
приводит после |
||
= |
|
+= |
|
|
|
|
|
|
|
|
+ |
|
|
|||
суммирования к следующей формуле: |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
( |
) + ( ) |
|
−1 |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∫ ( ) ≈ ( |
|
0 |
|
|
|
+ ∑ ( )). |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
=1 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Блок-схема метода прямоугольников представлена на рис.3.
Метод Симпсона (парабол)
Разбиение промежутка [ ; ] на четное число ( = ) отрезков поз-
воляет на каждой паре отрезков [ ; + ] заменить подынтегральную функцию параболой ( ) = + + . Площадь фигуры, ограниченной сверху параболой, считается по формуле:
+2
∫ ( 2 + + ) = 3 ( + 4 +1 + +2) .
Суммирование таких интегралов (площадей, ограниченных параболами) приводит к более точной, чем предыдущие, формуле:
∫ ( ) ≈ 3( 0 + 4( 1 + 3 + … + 2 −1) + 2( 2 + 4 + … + 2 −2) + 2 ) .
Увеличение числа разбиений приведёт к более точным результатам. При вычислении интегралов описанными методами оценить количество разбиений отрезка удается достаточно редко. В таком случае следует выполнить расчёты интеграла для шага h и h/2 и полученные значения сравнить.
6
|
|
|
/ |
|
|
Если для формулы Симпсона оценочная величина |
|
− |
больше за- |
||
|
|
|
|||
|
|
|
|||
данной точности ε, то приходится уменьшать шаг до h/4 и т.д., пока на какомто этапе не будет выполнено условие:
− /2 < . 15
Данный алгоритм позволяет вычислить значение интеграла с автоматическим выбором шага. Его схема представлена на рис.4.
Начало
Ввод a, b, ε
F(x)
h=(b-a)/n I1=0
= ( )+( ) 2
x=a+h, b-h, 2h
S=S+2f(x)+f(x+h)
Конец цикла x
I=2hS/3 R=|I-I1|/15 h=h/2
I1=I
нет |
|
да |
|||
|
|
R>ε |
|
|
Вывод I |
|
|
|
|||
|
|
|
|
|
|
Конец
Рис.4. Блок-схема алгоритма метода Симпсона
7
Для удобства программирования использована измененная формула Симпсона:
|
2 |
|
0− 2 |
|
2 −1(2) |
|
|
||
∫ ( ) ≈ |
( |
+ |
∑ |
(2 + |
)). |
||||
|
|
||||||||
|
3 |
2 |
|
|
|
+1 |
|
||
|
|
=1 |
|
|
|
||||
|
|
|
|
|
|
|
|||
|
|
|
2. Задание |
|
|
|
|||
Вычислить интеграл |
∫ |
( ) с заданной погрешностью по формулам |
|||||||
|
|
|
|
|
|
|
|
|
|
прямоугольников, трапеций, Симпсона.
3.Порядок выполнения лабораторной работы
1.Изучить свой вариант задания (см. с.10). Номер метода:
метод прямоугольников-1; метод трапеций – 2; метод Симпсона-3.
2.Разработать блок-схему алгоритма решения задачи.
3.Составить программу решения задачи.
3.1.Исходные данные: пределы интегрирования a,b, точность ε задавать при вводе. В результате вычисления должны быть получены значения интеграла , величина погрешности и шага интегрирования h.
3.2.Использовать подпрограмму-функцию для вычисления f(x).
3.3.Использовать подпрограмму для вычисления интеграла при заданном количестве разбиений N отрезка [ ; ].
4.Составить отчет по лабораторной работе.
Алгоритм вычисления интеграла с заданной точностью
1. |
Вычислить 0 = ( − )( ( ) + ( ))/2 и 2 – значение интеграла при 2-х |
|
разбиениях отрезка [ ; ] по заданному численному методу. |
2. |
Найти модуль разности значений этих интегралов = | 0 − 2| и сравнить с |
|
заданной погрешностью ε. |
3. |
Если модуль разности не превышает ε, то считают интеграл |
|
|
|
∫ ( ) |
вычисленным с заданной точностью. Значение интеграла равно 2.
8
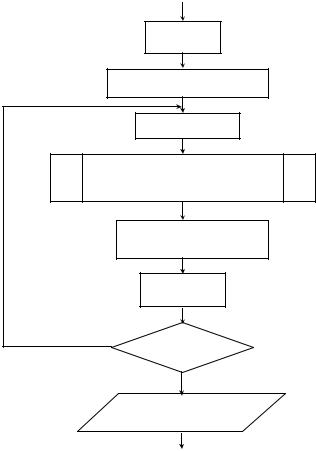
4.В противном случае вычислить 4 – значение интеграла при 4-х разбиениях отрезка [a, b] и сравнить 2 и 4 и т.д., пока точность ε не будет достигнута
(рис.5).
N=1
I0=(b-a)(f(a)+f(b))/2
N=2n
Подпрограмма вычисления I при заданном N
R=| I0-I2|
I0=I
нет
R<ε
да
Вывод I, N
Рис.5. Блок-схема алгоритма вычисления определённого интеграла
4.Контрольные вопросы
1.В чем заключается задача численного интегрирования?
2.Записать указанные преподавателем формулы вычисления интеграла численными методами.
3.Геометрическая интерпретация вычисления интеграла.
4.Объяснить алгоритм численного интегрирования с помощью различных методов.
9
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5. |
Варианты заданий |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Номер |
|
Функция |
|
Отрезок [; ] , |
Номер |
|||||||||||||||||||
Варианта |
|
|
|
|
|
|
|
|
|
|
f(x) |
|
|
|
|
|
|
|
|
точность ε |
метода |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
(2 + sin( )) |
[1;2], |
10−4 |
1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
2( ) + c2( ) |
[0,5;1], |
10−3 |
2 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
|
|
|
|
|
− 1 |
|
|
|
|
[0; 1,5], |
10−4 |
3 |
|||||||||||
4 |
|
sin( ) |
|
[0;1], |
10−4 |
1 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
5 |
|
|
|
|
|
|
|
|
|
sin( |
|
|
|
) |
|
|
|
[1; 2,5], |
10−3 |
2 |
||||
|
|
|
2 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
6 |
∙ ( ) |
|
[0;3], |
10−3 |
3 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
7 |
(1 + ln( )) |
|
[1;2], |
10−4 |
1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
8 |
|
√ 2 |
− 0,2 |
|
[1;2], |
10−4 |
2 |
|||||||||||||||||
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
9 |
|
|
|
|
|
|
|
|
|
|
23 |
|
|
|
|
|
|
|
[0;1], |
10−3 |
3 |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
10 |
|
|
|
|
2( ) |
|
|
|
|
[0; 1,7], |
10−3 |
1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
11 |
|
|
|
|
(( )2 |
|
[1; 2,7], |
10−4 |
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[ |
] |
−3 |
|
|
12 |
|
|
4(1+ |
2 |
) |
|
|
|
3 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
0;1 , |
10 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
2 − 1 |
|
|
|
|
|
|
|
|
||||||||||
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
[0;1], |
10−3 |
1 |
|||||||
|
|
|
|
|
2 + 1 |
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
( |
1 |
∙ ( ))3 |
|
|
|
|
|
|||||||||||||||
14 |
|
|
|
|
|
|
2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
[1;2], |
10−4 |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
15 |
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
[0;2], |
10−4 |
3 |
|||
|
|
|
|
|
|
|
3 + |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 |
|
|
|
