
202910
.pdf
|
x3 4 |
4 |
|
8 |
|
x3 8 |
|
|||
y ( |
|
) (x |
|
) 1 |
|
|
|
|
|
. В точке при x=0 производная не су- |
x2 |
x2 |
x3 |
x3 |
|||||||
ществует. Приравнивая выражение для производной нулю и решая полу-
ченное уравнение, получим стационарную точку x=2 . Таким образом, рас-
сматриваемая функция имеет две критические точки: при x=2 производная обращается в ноль, а при x=0 не существует. Эти точки разбивают числовую ось на три части: (- ,0), (0,2) и (2,+ ). Исследуем знаки производной:
при - <х<0 |
y(-1)=(-1-8)/(-1)=9, |
y'>0, |
функция возрастает; |
при 0<x<2 |
y(1)=(1-8)/1=-7, |
y'<0, |
функция убывает; |
при 2<x<+ |
y(3)=(27-8)/27=19/27, |
y'>0, |
функция возрастает. |
Следовательно, точка x=2 является точкой минимума, ymin=3. Точка x=0 не является точкой экстремума, ибо она не принадлежит области определения.
6. Находим интервалы выпуклости и вогнутости графика функции и точки перегиба. Для этого вычислим вторую производную:
y (1 x83 ) 24x4 . Так как вторая производная положительна при всех зна-
чениях аргумента из области определения, то график функции является всюду вогнутым и, следовательно, не имеет точек перегиба.
Исходя из полученных данных строим график функции (см. рис. 3).
21
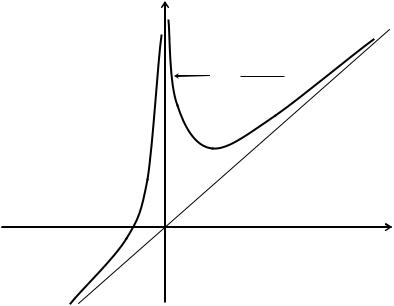
y
y x3 4 x2
 y=x
y=x
0 |
x |
Рис. 3
Упражнения
1. Найти интервалы возрастания и убываний и экстремумы функций:
1.1. y=2x3+3x2-36x+5, |
1.5. y x |
1 |
|
|
|||
x |
|||||||
|
|
|
|||||
1.2. |
y e3x4 4 x3 , |
1.6. y=xe2x-1. |
|||||
1.3. |
y=2+(x-3)6/7, |
1.7. y=log2(x4+5) |
|||||
|
|
1.8. y xe |
x4 |
||||
1.4. y=(x-5)6+3 |
4 |
|
|||||
2. Найти наибольшие и наименьшие значения функций на отрезках: |
|||||||
2.1. y=2x3+3x2-12x+2 |
на отрезке [-3,2], |
||||||
2.2. y=x2+4x+3 |
на отрезке [-1,1]. |
||||||
3. |
Определить промежутки выпуклости и вогнутости и точки перегиба гра- |
|
фиков функций: |
|
|
|
3.1. y=-2x3+24x2, |
3.4. y=(x+1)3, |
|
3.2. y=x4-12x3, |
3.5. y=(2x-4)4, |
|
3.3. y=xarctgx, |
3.6. y=ln(x2+1). |
4. |
Исследовать функции и построить их графики: |
|
|
|
22 |

4.1. y=2x3-9x2, |
4.3. у=x+e-x, |
||
4.2. y |
x |
4.4. y=x+arctgx. |
|
|
, |
||
x4 4 |
|||
|
4. Неопределенный интеграл |
||
Пример. Найти интеграл (3x4 |
6x2 5)dx . |
||
Пользуясь свойством интеграла от суммы, представим данный инте-
грал в виде суммы трех интегралов. Затем в каждом из полученных инте-
гралов вынесем постоянные множители (3, 6 и 5 соответственно) за знак ин-
теграла. Далее воспользуемся формулами основных табличных интегралов:
(3x4 6x2 5)dx 3x4dx 6x2dx 5dx 3 x4dx 6 x2dx 5 dx
53 x5 63 x3 5x C 53 x5 2x3 5x C .
Пример. Найти интеграл (5cos x 6ex )dx .
(5cos x 6ex )dx 5cos xdx 6exdx 5 cos xdx 6 exdx 5sin x 6ex C .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Пример. Найти интеграл |
2x5 3x2 4x x |
|
dx . |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
x3 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Представим подынтегральное выражение данного интеграла в виде |
|||||||||||||||||||||||||||||||||
суммы |
трех |
|
слагаемых, |
разделив числитель |
|
почленно |
|
на знаменатель: |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
2x5 3x |
2 4x x |
|
2x2 |
3 |
4x 1,5 |
. Используя далее свойства неопределенно- |
||||||||||||||||||||||||||||||
|
|
|
|
x3 |
|
|
|
|
x |
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
го интеграла, получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
2x5 |
3x2 4x x |
|
dx (2x2 |
|
3 |
4x 1,5 )dx |
2x2dx |
3 |
|
dx 4x 1,5dx |
|||||||||||||||||||||||
|
|
|
|
x3 |
|
|
|
|
|
|
|
x |
x |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2 |
|
x2dx 3 |
1 |
dx 4 |
|
|
x 1,5dx 2 |
x3 |
|
|
3ln | x | 4 |
x 0,5 |
|
|
|
C |
2 |
x3 |
3ln | x | |
8 |
|
C |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
x |
|
|
|
|
|
|
3 |
|
|
|
|
0,5 |
3 |
|
|
|
|
|
|
x |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
.
23

Пример. Найти интеграл |
x2 cos x3dx |
методом подведение функции |
|||||||||||
под знак дифференциала. |
|
|
|
|
|
|
|
|
|||||
Преобразуем |
заданный |
интеграл |
|
с |
|
учетом |
того, |
что |
|||||
x2dx d |
x3 |
|
1 |
dx3 : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
3 |
|
|
|
|
|
|
|
|
|
|||
|
|
x2 cos x3dx cos x3 x2dx cos x3d |
x3 |
|
1 |
cos x3dx3 . |
|
||||||
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
3 |
|
|
||
В полученном интеграле переменной интегрирования служит выражение x3.
Относительно этой переменной получается табличный интеграл от косинуса
cos x3dx3 sin x3 C . Следовательно,
x2 cos x3dx 13 cos x3dx3 13 sin x3 C .
Пример. Найти интеграл (3x 6)21dx методом замены переменной.
Введем новую переменную t следующим образом: t=3x+6. Дифференцируя обе части равенства, получим: dt=(3x+6)'dx=3dx. Выразим дифференциал dx
старой переменной через дифференциал dt новой: dx= |
dt |
. Подставляя по- |
||||||||
|
|
|||||||||
|
|
|
|
|
|
|
3 |
|
|
|
лученные результаты в исходный интеграл, получим: |
|
|
|
|
||||||
(3x 6)21dx t21 |
dt |
|
1 |
t21dt |
1 |
t22 C |
1 |
|
t22 C . |
|
|
|
3 22 |
|
|
|
|||||
3 |
3 |
|
66 |
|
|
|||||
Ответ необходимо выразить через старую переменную x. Подставим t=3x+6
в полученный результат интегрирования и получим
|
|
(3x 6)21dx |
1 |
(3x 6)22 C . |
||||
|
|
66 |
||||||
|
|
|
|
|
|
|
|
|
Пример. Найти интеграл x2 cosx3dx методом замены переменной. |
||||||||
Пусть |
t x3 . Тогда |
dt 3x2dx |
и |
x2 dx |
1 |
dt . Следовательно, |
||
|
||||||||
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
24 |
|
|
|

x2 cos x3dx 13 cos tdt 13 sin t C 13 sin x3 C .
Пример. Найти интеграл x sin dx методом интегрирование по частям.
Этот интеграл относится к первому типу. Поэтому положим u=x, dv=sinxdx. Тогда du=dx, v=-cosx. Используя формулу интегрирования по частям, получаем
xsin xdx x cos x cos xdx x cos x sin x C .
Пример. Найти интеграл ln xdx методом интегрирование по частям.
Поскольку данный интеграл следует отнести ко второму типу, то при-
мем, что u=lnx, dv=dx. Тогда du= dxx , v=x. Применяя формулу интегриро-
вания по частям, получаем
ln xdx x ln x x dxx x ln x dx x ln x x C .
Пример. Вычислить интеграл ex sin xdx методом интегрирование по частям.
Данный интеграл относится к третьей группе. Обозначим его через I.
Примем, что u=ex, dv=sinxdx. Тогда du=exdx, v=-cosx. Следовательно,
I ex sin xdx ex cos x ex cos xdx.
Применим метод интегрирования по частям к интегралу ex cos xdx , входя-
щему в правую часть полученного выражения, считая, что u=ex и dv=cosxdx.
Тогда du=exdx, v=sinx и
Iex cos x (ex sin I ) ex cos x ex sin x I .
Врезультате получено линейное уравнение относительно неизвестного ин-
теграла I. Решая это уравнение, получим искомый интеграл
25

I ex (sin x cos x) C . 2
На последнем шаге решения к первообразной была прибавлена произволь-
ная постоянная.
Упражнения
1. Найти интегралы методом непосредственного интегрирования:
|
(2sin x 3cos x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
)dx |
||||||||||||||||||||
1.1. |
1.5. |
(2x3 3 |
|
|
|
x |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 |
|
|
|
|||||
1.2. |
(3ex |
5sin x)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
1.6. |
|
( |
2 |
|
|
|
5 |
|
3 |
|
|
|
|
x |
|
)dx |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x5 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x2 |
|
x |
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
5 |
3x |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
( |
|
|
|
|
|
|
3 2x )dx |
|
|
|
2x |
|
x |
|
|
|
|
|
|
|
||||||||||||||||
1.3. |
|
|
|
|
|
|
1.7. |
|
|
|
dx |
||||||||||||||||||||||||||
|
cos |
2 |
x |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
x2 |
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
3 |
|
|
|
|
1.8. |
|
|
|
|
|
|
3 |
|
|
|
2x |
|
|
|
|
|
|
|
|
|
||||||||
1.4. |
( |
|
|
|
4 cos x |
2x2 )dx |
( |
|
|
|
|
|
|
|
|
|
|
x )dx |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
x |
2 |
|
|
|
|
||||||||||||||||||||||||
|
x2 |
1 |
|
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2. |
Найти интегралы методом подведение функции под знак дифференциала: |
|||||||||||||||||||
|
2.1. |
(x3 1)( x4 4x 3)4 dx |
2.4. |
tgxdx |
|
|
|
|
||||||||||||
|
|
|
|
|
x3 |
|
|
|
|
|
2 |
|
|
|
|
|
||||
|
2.2. |
|
|
|
|
|
dx |
2.5. |
xe 2 x |
3dx |
||||||||||
|
( x4 2)3 |
|||||||||||||||||||
|
|
|
|
|
|
|
2.6. |
(x 1)sin( x2 2x)dx |
||||||||||||
|
2.3. |
|
sin( 3x) cos(3x)dx |
|||||||||||||||||
3. |
Найти интегралы методом замены переменной: |
|
|
|
|
|
||||||||||||||
|
|
sin( 2 5x)dx |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
3.1. |
3.4. |
x3 |
|
x4 |
6dx |
||||||||||||||
|
3.2. |
x3 (2 3x4 )6 dx |
3.5. |
sin( x3 |
3)x2dx |
|||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x 2 dx |
|
|
|
|||||||
|
3.3. |
|
x |
dx |
|
3.6. |
|
e |
|
|
||||||||||
|
3 |
4 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
x |
|
|
|
3x 2 |
|||||||||||||
4. |
Найти интегралы методом интегрирования по частям: |
|||||||||||||||||||
|
4.1. |
x cos2xdx |
4.4. |
(x2 |
2x 5) ln xdx |
|||||||||||||||
|
4.2. |
e3x x2dx |
4.5. |
xarctg(x)dx |
||||||||||||||||
26

4.3. (x2 3x 1) cos xdx |
4.6. e2 x cos xdx |
5. Определенный интеграл
1
Пример. Вычислить определенный интеграл x4 dx .
0
Одной из первообразных для функции y=x4 является функция x5 , по-
5
этому по формуле Ньютона – Лейбница имеем:
1 |
x |
5 |
5 |
|
0 |
5 |
|
1 |
|
|
|
|
|
|
x4 dx |
|
|10 |
1 |
|
|
|
. |
|
|
|
|
|||
5 |
|
|
|
|
|
|
|
|
||||||
0 |
5 |
5 |
|
5 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример. Вычислить определенный интеграл |
|
dx . |
|
|
||||||||||
1 x2 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
||
Функция arctgx является одной из первообразных для функции |
1 |
, |
||||||||||||
|
||||||||||||||
1 x2 |
||||||||||||||
следовательно, по формуле Ньютона – Лейбница получим:
1 |
1 |
dx arctgx |10 arctg1 arctg0 |
|
0 |
. |
|
|
||||||
1 x2 |
4 |
|||||
0 |
|
|
4 |
b
Пример. Вычислить определенный интеграл cos xdx .
a
b
Поскольку cos xdx sin x C , то cos xdx sin x |ba sin b sin b .
a
Пример. Вычислить интеграл (3sin x 2x)dx .
0
Воспользовавшись свойствами, представим исходный интеграл в виде разности двух интегралов, а затем вынесем постоянные множители за знаки интегралов:
27

|
|
|
|
|
(3sin x 2x)dx 3sin xdx 2xdx 3 sin xdx 2 xdx . |
||||
0 |
0 |
0 |
0 |
0 |
Определим первообразные для каждой из подынтегральных функций по таблице основных интегралов и воспользуемся формулой Ньютона-
Лейбница:
|
(3sin x 2x)dx 3cos x | |
2 |
x |
2 |
| |
3cos 3cos 0 2 |
0 6 2 . |
|
|
|
|||||||
|
|
|||||||
|
0 |
2 |
0 |
|
|
|||
0 |
|
|
|
|
|
|||
|
|
|
|
|
|
1 |
|
|
Пример. |
Вычислить интеграл 6e3x2 1 xdx методом подведение функ- |
|||||||
|
|
|
|
|
|
0 |
|
|
ции под знак дифференциала.
Сперва внесем x под знак дифференциала. Для этого проинтегрируем
его xdx |
x2 |
C . Тогда |
xdx d |
x2 |
|
1 |
dx2 |
. Далее воспользуемся тем, что |
|
|
|
||||||
2 |
|
2 |
|
2 |
|
|
||
под знак дифференциала можно внести постоянный множитель и добавить произвольную постоянную:
1 |
1 |
x |
2 |
1 |
1 |
1 |
|
|
6e3x2 |
1 xdx 6 e3x2 1d |
|
3 e3x2 1dx2 |
e3x2 |
1d (3x2 ) e3x2 1d (3x2 |
1) . |
||
2 |
||||||||
0 |
0 |
0 |
0 |
0 |
|
|||
В преобразованном интеграле переменной интегрирования служит выраже-
ний 3х2+1. Интеграл относительно этого выражения является табличным,
поэтому, применяя формулу Ньютона-Лейбница, получим:
1 |
|
|
|
|
|
6e3x2 1 xdx |
e3x2 1 |
|10 e4 e |
|||
0 |
|
|
|
|
|
|
e 2 |
|
dx |
|
|
Пример. Вычислить интеграл |
ln 3 2x |
методом замены перемен- |
|||
x |
|||||
|
12 |
|
|
||
ной.
Введем новую переменную t следующим образом: t=ln2x. Продиффе-
ренцировав обе части этого равенства, находим связь между дифференциа-
28

лами новой и старой переменной: dt=(ln2x)'dx= dxx . При замене переменной интегрирования необходимо одновременно заменить и пределы интегриро-
вания. Учитывая связь между новой и старой переменными, получим, что
если x=1/2, то t ln( 2 12 ) ln 1 0 , а если x=e/2, то t ln( 2 2e ) ln e 1 . Под-
ставим в исходный интеграл новую переменную, выражение для частного
dx через дифференциал новой переменной dt и заменим пределы интегри- x
рования. В результате получим интеграл
|
|
|
|
|
|
|
|
e 2 |
|
|
dx |
1 |
|
|
|
t |
6 |
|
|
|
1 |
|
|
0 |
|
1 |
|
|||||||
|
|
|
|
|
|
|
|
ln 3 2x |
t5dt |
|
|
|10 |
|
|
. |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
12 |
|
|
|
x |
0 |
|
|
6 |
|
|
|
6 |
|
|
6 |
6 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
dx |
|
|
|
|
|
||||
Пример. Вычислить интеграл |
sin |
|
x |
|
|
|
методом замены перемен- |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
x |
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
, dt |
dx |
|
|
|
и |
dx |
|
2dt . Определим новые пределы Инте- |
|||||||||||||||||||||||
Пусть |
x |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
2 |
|
|
x |
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
грирования. Если x= 2/4, то t= /2, а если x= 2, то t= . Поэтому |
||||||||||||||||||||||||||||||||||
2 |
|
|
dx |
|
|
2 cos t | 2 cos 2 cos 0 2 2 . |
||||||||||||||||||||||||||||
sin |
x |
|
2 sin tdt |
|||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||||
2 |
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
||||||
4 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример. Вычислить интеграл |
xex dx методом интегрирования по ча- |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
стям.
Введем функции u и v следующим образом: u=x и dv=exdx. Тогда du=dx, а v=ex. Применяя формулу интегрирования по частям, получим:
2 |
2 |
|
xex dx xex |12 |
ex dx xex |12 |
ex |12 ex (x 1) |12 e2 (2 1) e1 (1 1) e2 . |
1 |
1 |
|
|
|
29 |

Пример. Вычислить площадь криволинейной трапеции, ограниченной графиком функции y=3x2, осью абсцисс и прямыми x=1 и x=2.
2 |
2 |
x |
3 |
|
|
S 3x2dx 3 x2dx 3 |
|
|12 x3 |12 23 13 8 1 7 . |
|||
3 |
|||||
1 |
1 |
|
|||
Пример. Вычислить площадь фигуры, ограниченной линиями y=x2 и y 
 x .
x .
Найдем точки пересечения графиков данных функций. Для этого ре-
шим систему уравнений
y = x2
y 
 x .
x .
Приравнивая правые части этих уравнений, получим:
x2 
 x , или
x , или 
 x(x3
x(x3 2 1) 0 .
2 1) 0 .
Произведение обращается в ноль, если один из сомножителей равен нулю.
Приравнивая каждый из сомножителей нулю, получаем два корня x=0 и x=1.
На отрезке [0,1] график функции y |
|
|
лежит выше графика функции y=x2, |
|||||||||||||||||||||||||||||||||
x |
||||||||||||||||||||||||||||||||||||
поэтому |
|
xdx x2dx [2 x3 2 1 x3 ] |10 2 13 2 |
113 |
1 . |
|
|
||||||||||||||||||||||||||||||
S ( x x2 )dx |
|
|
||||||||||||||||||||||||||||||||||
1 |
|
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
0 |
0 |
3 |
3 |
|
|
3 |
|
|
|
3 |
|
3 |
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Пример. Найти длину дуги кривой y |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
x 2 |
от x=0 до x=3. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
3 |
|
|
2 |
|
3 |
|
|
1 |
|
|
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Найдем |
производную данной |
функции |
y |
( 3 x |
) |
3 |
2 x |
|
x |
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Подставим производную в формулу для длины дуги кривой и проведем ин-
тегрирование. Дописывая под знаком дифференциала единицу, получаем:
|
|
|
|
|
1 xd (1 x) 2 |
3 |
|
||
L |
1 ( |
x )2 dx |
1 xdx |
(1 x) 2 |
|03 |
||||
3 |
|
3 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0 |
|
0 |
0 |
3 |
|
|
|||
|
|
|
|
30 |
|
|
|
|
|
