
Методика научных исследований и патентоведение (90
..pdfгде хьх2...хп —варианты признака; n —число периодов.
2. Показатели изменчивости признака – среднее квадратическое отклонение (δ), коэффициент изменчивости (Cv).
Установление степени разнообразия признака в популяциях имеет важное значение в генетическом анализе популяций и в селекции. Именно величиной изменчивости определяется возможность улучшения путем отбора лучших животных в племенных стадах.
В зависимости от величины изменчивости все хозяйственно полезные признаки животных, по которым ведется селекция, подразделяют на признаки с низкой изменчивостью (коэффициент изменчивости находится в пределах 1 — 15 %), средней (16—25 %) и высокой изменчивостью (26 % и более). При высокой изменчивости какого-либо признака лучшие и худшие показатели будут существенно отличаться от средней арифметической, что даст возможность постоянного повышения среднего уровня признака по стаду за счет отбора для воспроизводства лучших особей. В то же время возможность селекции на улучшение признака, характеризующегося низкой изменчивостью, практически исключается. Это связано с тем, что показатели селекционного признака будут очень близкими к средней, и поэтому отобрать лучших особей из стада весьма сложно.
При изучении изменчивости (вариабельности) признака особей данной совокупности применяют следующие параметры: лимит (lim =xmax — х min), среднее квадратическое отклонение ( ), коэффициент вариации (CV, %).
Чем больше разность между максимальной и минимальной вариантой, тем значительнее изменчивость признака. Однако эти показатели недостаточны, так как особи с такими показателями часто бывают нехарак-
терны для данной популяции. Наиболее часто употребляемыми в практической селекции показателями вариабельности признака являются среднее квадратическое (стандартное) отклонение и коэффициент изменчивости .
Среднее квадратическое отклонение позволяет судить о степени разно-
образия признака в абсолютных величинах. Чем больше величина , тем выше
21

изменчивость. Вся изменчивость признака укладывается от средней арифметической в пределах ±3 , (правило плюс-минус трех сигм), поэтому средняя арифметическая, уменьшенная и увеличенная на З дает практически крайние варианты признака. Так, если « удоев» равна 600 кг, а х = 4000 кг, то мини-
мальный удой у коров в такой совокупности, вероятнее всего, будет равен 2200
кг ( х - 3 = 4000 - 3 • 600 = 2200), а максимальный — 5800 кг ( х + 3 = 4000 + 3-600 = 5800).
Коэффициент вариации (Cv) выражает степень изменчивости признака в процентах от величины средней арифметической. Формула для вычисления коэффициента вариации следующая:
Cv = 100 %
Пример. При проведении исследований получили следующие результа-
ты в изучаемых группах (табл.6). Для определения средних величин в груп-
пах ( Х ), ошибок средних арифметических (m), стандартных отклонений ( ) можно воспользоваться пакетом анализа в программе Microsoft Office Excel. Все полученные данные заносятся в программу столбиком отдельно по каж-
дой группе.
Таблица 6- Показатели продуктивности исследуемых групп.
|
Контрольная группа, |
n = 20 |
|
|
Опытная группа, |
n = 20 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
Жирно- |
Молоч- |
|
Белко- |
Живая |
|
Жирно- |
Молоч- |
Белко- |
Живая |
Удой, |
молоч- |
|
вомо- |
Удой, |
молоч- |
вомо- |
||||
ный |
|
масса. |
ный |
масса. |
||||||
кг |
ность, |
|
лоч- |
кг |
ность, |
лоч- |
||||
жир, кг |
|
кг |
жир, кг |
кг |
||||||
|
% |
|
ность |
|
% |
ность |
||||
|
|
|
|
|
|
|
||||
1 |
2 |
3 |
|
4 |
5 |
6 |
7 |
8 |
9 |
10 |
5858 |
3,55 |
207,8 |
|
2,94 |
487 |
5689 |
3,73 |
212,0 |
2,99 |
500 |
4899 |
3,39 |
166,1 |
|
2,96 |
468 |
4578 |
3,42 |
156,5 |
2,89 |
489 |
4595 |
3,55 |
163,2 |
|
2,99 |
487 |
4408 |
3,55 |
156,4 |
3,04 |
465 |
5259 |
3,44 |
180,9 |
|
2,97 |
489 |
4797 |
3,73 |
178,7 |
2,97 |
512 |
4695 |
3,36 |
157,6 |
|
3,01 |
481 |
4771 |
3,61 |
172,1 |
3,02 |
497 |
5354 |
3,57 |
191,2 |
|
2,98 |
487 |
4068 |
3,77 |
153,3 |
2,93 |
467 |
3962 |
3,62 |
143,4 |
|
2,97 |
452 |
3837 |
3,75 |
144,0 |
2,98 |
480 |
4963 |
3,80 |
188,6 |
|
2,96 |
487 |
4210 |
3,95 |
166,5 |
2,97 |
520 |
6337 |
3,43 |
217,3 |
|
2,98 |
468 |
4592 |
3,68 |
168,9 |
3,02 |
497 |
4840 |
3,48 |
168,3 |
|
2,94 |
485 |
5456 |
3,67 |
200,4 |
3,01 |
510 |
3997 |
3,81 |
152,4 |
|
2,99 |
487 |
4210 |
3,55 |
149,5 |
3,00 |
495 |
6130 |
3,39 |
207,7 |
|
2,98 |
489 |
5501 |
3,64 |
200,2 |
2,97 |
485 |
4295 |
3,77 |
162,0 |
|
2,96 |
465 |
5446 |
3,56 |
194,1 |
3,04 |
487 |
22
|
|
|
|
|
|
|
Продолжение таблицы |
6 |
|||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
8 |
9 |
|
10 |
5681 |
3,69 |
209,6 |
2,93 |
459 |
4468 |
3,62 |
|
161,7 |
2,94 |
|
504 |
5702 |
3,70 |
211,1 |
2,95 |
478 |
4370 |
3,73 |
|
163,0 |
2,97 |
|
510 |
4805 |
3,76 |
180,8 |
2,98 |
434 |
4519 |
3,81 |
|
172,0 |
2,97 |
|
518 |
4970 |
3,36 |
167,0 |
2,90 |
533 |
3968 |
3,77 |
|
149,6 |
2,92 |
|
491 |
4761 |
3,65 |
173,9 |
2,96 |
480 |
3974 |
3,73 |
|
148,3 |
2,95 |
|
510 |
5685 |
3,53 |
200,4 |
2,97 |
511 |
5019 |
3,72 |
|
186,6 |
3,01 |
|
519 |
5011 |
3,66 |
183,5 |
2,95 |
525 |
4843 |
3,87 |
|
187,5 |
3,02 |
|
510 |
В случае, когда на персональном компьютере в программе Excel отсутствует пакет анализа, для его подключения необходимо выбрать в меню сер-
вис - надстройки – отметить галочкой «пакет анализа» (рис. 1).
Рисунок 1 – Выбор пакета анализа После того, как занесены все данные по группам, приступают к стати-
стической обработке результатов в группе. В верхней панели инструментов выбирают функцию «сервис» - «анализ данных». После этого появится диалоговое окно где следует выделить инструмент анализа «описательная статистика» - «ОК» (рис.2).
23
Рисунок 2– Выбор описательной статистики Появляется диалоговое окно (рис.3), в разделе «входные данные» -
входной интервал нажать на клавишу с красной стрелкой (окно сворачивается).
Рисунок 3 - Входные данные Выделить весь цифровой материал одной из групп в «бегущую» рамоч-
ку – enter. Вновь появляется диалоговое окно «описательная статистика» (рис.4). В разделе «параметры вывода» на выходном интервале в кружочке поставить точку и нажать на клавишу с красной стрелкой (окно сворачивается).
24
Рисунок 4– Выходной интервал
Выделить «бегущую» рамочку на любом свободном месте – enter. Снова появляется диалоговое окно – в параметре «итоговая статистика поставить «галочку» - ОК. (рис. 5).
Рисунок 5 – Итоговая статистика В итоге получается результат следующего вида (рис.6), где представле-
ны обработанные данные в столбцах по всем пяти изучаемым показателям
(удой, жирномолочность, количество молочного жира, белковомолочность, живая масса).
25
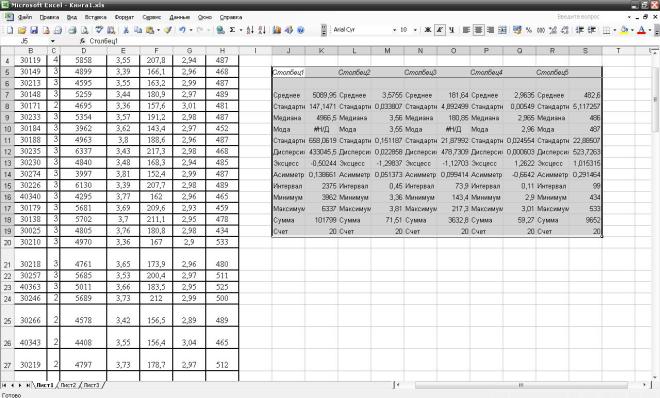
Рисунок 6 – Итоговый результат Как правило, для проведения анализов полученных результатов нужны
данные первой строки – средняя арифметическая, вторая строка – ошибка средней арифметической, пятая строка – среднее квадратическое отклонение. В последней строке показан объём выборки (n). Выписывают полученные результаты – например (столбец 1) средний удой по группе, ошибка средней арифметической составили 5089,96±147,15. Значение «среднее квадратиче-
ское отклонение» необходимо для расчёта коэффициента вариации (Cv). Такой же порядок обработки цифровых данных проводят с другими группами.
Биометрические методы анализа дают возможность изучить связь между варьирующими признаками, определить ее величину и направление. Применение показателей связи между признаками имеет практическое зна-
чение в селекционной работе и прогнозировании эффекта селекции. Отбор сельскохозяйственных животных для воспроизводства осуществляют по ограниченному числу признаков. Большинство признаков и свойств животных находятся в определенной взаимосвязи. Например, существует связь между удоем и содержанием жира в молоке коров, между настригом и гу-
26
стотой шерсти у овец, между живой массой несушек и массой яйца и т. д., поэтому отбор животных по какому-либо одному признаку оказывает косвенное влияние и на другие признаки. Таким образом, при выявлении связей между признаками можно проводить косвенную селекцию (показатели связи).
3. Показатели связи между признаками – коэффициент фенотипической корреляции (r), коэффициент регрессии (R)
Коэффициент корреляции (r) — основной биометрический показатель, позволяющий определять величину и направление связи между признаками. Он показывает величину связи между двумя, тремя и большим числом признаков. Величина этого коэффициента принимает дробное выражение в пределах от 0 до ± I. Чем ближе показатель к единице, тем больше связь между коррелирующими признаками. По форме корреляция может быть прямолинейной и криволинейной, по направлению — положительной (прямой) и отрицательной (обратной), на что указывает знак «плюс» или
«минус». Приняты следующие тесноты связи: r = 0,1 — 0,3 — связь слабая; 0,3 — 0,5 — умеренная; 0,5 — 0,7 — заметная; 0,7 — 0,9 — высокая; 0,9 — 0,99 — весьма высокая. Чем ближе он по абсолютной величине к 1, тем сильнее связь. Связь, наблюдаемая между величинами двух признаков, называется фенотипической корреляцией, а связанная с ней регрессия показывает,
вкакой степени средняя величина одного признака зависит от другого
4.Критерий достоверности разности средних арифметических.
При сравнении двух групп, двух и более параметров вычисляют критерий достоверности разности между группами (td), выводят вероятность достоверности результатов (Р)
td |
|
|
х1 х2 |
|||||
|
|
|
|
|
|
|
||
m |
2 |
|
m |
2 |
|
|||
|
|
|
х |
|
х |
|
||
|
|
|
1 |
2 |
||||
Вычисленный критерий достоверности (td) сравнивают со значением критерия достоверности в таблице Стьюдента (приложение А) при трех уровнях вероятности (Р ≥ 0,95; Р ≥ 0,99; Р ≥ 0,999) или уровнях значимости
27

события (Р ≤ 0,05; Р≤ 0,01; Р ≤ 0,001). С помощью уровня значимости можно установить, в каком проценте случаев возможна ошибка в результатах. Например, если уровень значимости Р = 0,05, это значит, что в силу случайности ошибка будет в 5 % случаев.
Нужную строку в таблице Стьюдента находят по формуле:
ν = n1 + n2 – 2,
где п1 и п2 - объем сравниваемых выборок.
Для биологических признаков разницу между средними арифметическими принято считать статистически достоверной в тех случаях, когда Р ≤ 0,05. Если же Р > 0,05, разница является статистически недостоверной.
Пример: Изучается эффективность влияния микроэлементов при откорме бычков. Сформированы две группы (опытная и контрольная) по 14 голов каждая.
По окончании опыта при биометрической обработке данных получены следующие результаты:
- средняя живая масса животных опытной группы Х 1 = 300 кг;
- средняя живая масса животных контрольной группы Х 2 = 260 кг;
- ошибки средних арифметических в опытной и контрольной группах соответственно равны:
mх1 = 9 кг, mх2 = 7 кг.
Разница в средних величинах живой массы животных опытной и контрольной групп составила 40 кг (d = 300 - 260). Достоверно ли это разли-
чие, закономерно ли оно? Для ответа на этот вопрос вычисляем критерий достоверности различий (td):
td |
|
|
х1 |
х2 |
|
300 260 |
3,5 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
m |
2 |
|
|
m |
2 |
|
|
92 72 |
|||||||
|
|
|
х |
|
|
х |
|
|
|
|
|||||
|
|
|
1 |
2 |
|
|
|
|
|
|
|||||
Сравниваем вычисленный критерий (td) с критериями таблицы Стьюдента. Для этого определяем число степеней свободы (ν):
ν = n1 + n2 – 2 = 14 + 14 -2 = 26.
28
В таблице находим строку 26 с указанными в этой строке значениями критерия достоверности, соответствующими трем уровням вероятности /
значимости |
|
Для ν = 26 при Р ≥ 0,95 / ≤ 0,05 |
t = 2,06 |
Р ≥ 0,99 /≤ 0,01 |
t = 2,78 |
Р ≥ 0,999 / ≤ 0,001 |
t = 3,71 |
Вычисленный критерий достоверности разности (td = 3,5) больше табличных значений критерия при Р = 0,95 и Р = 0,99, но меньше критерия при Р = 0,999. Следовательно, разность средних арифметических опытной и контрольной групп бычков (d = 40 кг) достоверна с вероятностью Р ≥ 0,99 (или со значимостью Р ≤ 0,01). Это значит, что положительное влияние микроэлементов на приросты животных в опытной группе будет эффективным и на большом числе откармливаемых бычков, т.е. в генеральной совокупности.
Биометрическая обработка данных повышает объективность выводов и заключений по результатам исследований, делает работу в каче-
ственном отношении более полноценной, соответствующей современным требованиям информационного представления.
Тема 7. Основы патентоведения
В процессе научной деятельности научный работник представляет результаты своей работы – селекционное достижение, полезная модель, образец и.т.д. на которые он имеет право оформить патент (охранный документ).
Селекционным достижением является - сорт растений, порода животных. Порода - группа животных, которая независимо от охраноспособности обладает генетически обусловленными биологическими и морфологическими свойствами и признаками, причем некоторые из них специфичны для данной группы и отличают ее от других групп животных. Охраняемыми категориями породы являются тип, кросс линий;
племенное животное - животное, предназначенное для воспроизводства породы;
29
племенной материал - племенное животное, его гаметы или зиготы (эмбрионы);
товарное животное - животное, используемое в целях, отличных от целей воспроизводства породы;
Право на селекционное достижение охраняется законом и подтвержда-
ется патентом на селекционное достижение. Патент удостоверяет исключительное право патентообладателя на использование селекционного достижения. Селекционное достижение, на которое Госкомиссией выдан патент, регистрируется в Государственном реестре охраняемых селекционных достижений. Патент выдается на селекционное достижение, отвечающее критери-
ям охраноспособности. Критериями охраноспособности селекционного достижения являются:
а) новизна - порода считается новой, если на дату подачи заявки на выдачу патента племенной материал данного селекционного достижения не продавались и не передавались иным образом другим лицам.
б) отличимость - селекционное достижение должно явно отличаться от любого другого общеизвестного селекционного достижения, существующего к моменту подачи заявки.
в) однородность - животные породы должны быть достаточно одно-
родны по своим признакам с учетом отдельных отклонений, которые могут иметь место в связи с особенностями размножения;
г) стабильность - селекционное достижение считается стабильным,
если его основные признаки остаются неизменными после неоднократного размножения или в случае особого цикла размножения, в конце каждого цикла размножения.
Право на подачу заявки на выдачу патента принадлежит селекционеру или его правопреемнику. Заявка подается в Госкомиссию. Заявка может быть подана несколькими заявителями, если они совместно вывели, создали или выявили селекционное достижение или являются правопреемниками авторов.
30
