Поверхностное моделирование.

Модель поверхностного типа описывается в терминах точек, линий и поверхностей. В отличие от каркасной модели она обеспечивает:

- точное представление криволинейных граней;

- автоматическое распознавание граней и их закраску;

- автоматическое удаление невидимых линий;

- распознавание особых линий на гранях (отверстий и т.д.);

- обнаружение столкновений между объектами.

Метод поверхностного моделирования наиболее эффективен при проектировании и изготовлении сложных криволинейных поверхностей (корпусов автомобилей и др.). При этом можно использовать:

- базовые геометрические поверхности (плоскости, цилиндры, кубы, результат перемещения образующей кривой в заданном направлении и т.д.);

- поверхности вращения (результат вращения линии вокруг оси);

- пересечения и сопряжения поверхностей;

- аналитические поверхности (задаются математическим уравнением).

Твердотельное (объемное, сплошное) моделирование.

В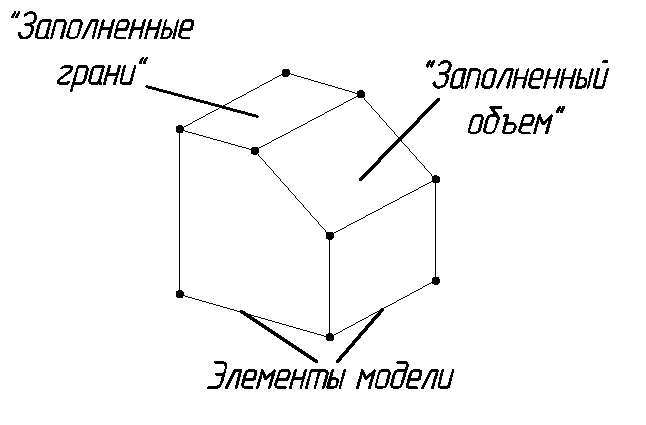 этих моделях в явной форме содержатся сведения о принадлежности элементов модели внутреннему или внешнему по отношению к детали пространству. Можно говорить о массе этих деталей.

Математические модели геометрического образа любой машиностроительной детали.

Любое изделие рассматривается как система. Базовыми элементами системы являются сами детали. Поэтому, когда рассматривается сложная система, она представляется в своей иерархии состоящей из целого ряда деталей. В свою очередь любую деталь в этой иерархии также можно рассматривать как встроенную систему. Ее можно расчленить на элементы различной степени сложности, вплоть до первичных элементов в виде отверстий, выступов, пазов и т.д. Эти элементы имеют простейшую форму, которую задают в виде примитивов, таких как плоскости, цилиндры, сферы, конусы. При построении модели детали ее представляют в форме последовательности упорядоченных множеств – картежей.

Математическая модель i–того элемента детали:

где картежи – сведения общего характера об элементе детали (шифр, номер ГОСТа, назначение);

– сведения, которые характеризуют количественные параметры элемента (размеры, предельные отклонения, посадки и т.д., характер соединения этого элемента со смежным), для которого строится математическая модель;

– сведения, отражающие отклонение реальной формы моделируемого элемента от заданных в модели (отклонение от прямолинейности, от цилиндричности и т.д.).

Для получения полной характеристики математической модели детали необходимо задание системы параметров детали ( – системный параметр детали). Они задают математические отношения между базовыми элементами, входящими в деталь. Эти отношения между элементами детали можно сделать (при выводе модели детали) введением определенной системы координат для рассматриваемой детали (декартовой, полярной). После этого математическая модель детали представляет собой набор сведений:

Граф иерархии элементов детали.

Любая деталь состоит из целого ряда граней (…, G _i-1 , G _i , G _i+1 ,…). Носителем грани является параметр Q _i , который имеет свое математическое описание (плоскость, сфера и т.д.). Любая грань в детали окантована граничным контуром N (набор прямых ломаных линий, образующихся за счет пересечения друг с другом любых смежных граней). Носителем граничного контура является параметр В ⁱ_j , который имеет свое математическое описание. Граничный контур как правило состоит из ребер R ⁱ_s (в основном прямые линии). Любое ребро в системе координат детали имеет начальную и конечную точки (V ^Н₁₁ и V ^К₁₁), которые определяют положение этого ребра. Каждое ребро имеет свой носитель В^К_i (уравнение прямой), расположенный в пространстве. Любой носитель (грани, граничного контура, ребер) может быть представлен в виде:

Так как носителем грани является плоскость, то:

– картеж сведений в виде коэффициентов.

Поскольку грань – поверхность второго порядка (цилиндр, тор и т.д.), то:

Например, грань является окружностью, тогда:

Математическая модель ребер может быть получена пересечением:

Рассмотрим структуры массивов:

<> - код поверхности.

Тип поверхности	Код
Плоскость	1
Цилиндрическая поверхность	2
Коническая поверхность	3
Сферическая поверхность	4
Тороидальная поверхность	5
Поверхность вращения, образованная дугой, центр которой не лежит на оси вращения	6
Эллипсоид вращения	7
Гиперболоид вращения	8
Параболоид вращения	9