Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Владимирский государственный университет им. Столетовых

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

ИЗБРАННЫЕ ВОПРОСЫ АЛГЕБРЫ ПОЛИНОМОВ (110

..pdf

Скачиваний:

Добавлен:

15.11.2022

Размер:

705.94 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Система имеет вид:

					3	3 1 2 8,
				1		3 1 2 8,
					2
					2	2 2 4.
				1		2 2 4.
Найдем 2 из второго уравнения и подставим в первое:
		1					3			1	2
			2	2 ,			1	3	1		1	2	8 ,


	2	2	1							2

1	3	6		8	,	3	12		16 0 .
			1					1
2	1					1

1 2 является корнем этого уравнения, тогда 3 12 16делится на

1 2 нацело:

						3											1 2
						3		12						16			1 2								8
								12						16
					1							1								2	2		1
																				1			1
						3		2 2
						3		2 2
					1						1
									2 2				12					1		16
											1							1

									2 2				4			1
											1					1			16
														8 1					16
														8 1					16
														8 1					16
																0
3	12			1	16 (									1	2)( 2 2										1	8) 0 ;
1				1										1						1					1
																			2
1 2 0																1			2					1			2
		2				8					0	1							2								4		,
2		2			1	8					0													1			4
	1				1														4
																			4
																1
			1		2
			1				1															1 2
							1															1 2
										4	2 0														0
										4	2 0
			2				2															2
							2															2						.
																												.
					4																			4
					4																			4
			1				1															1			6
							1																		6
										16 2 6											2
										16 2 6											2
			2				2
							2
		х у 2																		х у 4
													или															.
		ху 0																		ху			6

х ,

у являются корнями уравнения z2 2z 0 или

z 4z 6 0. По

теореме Виета:

х 0

х 2

i 2

или

, или

х 2

, или

х 2

у 2

у 0

у 2

i 2

у 2

i 2

З а д а ч а 5. Решить иррациональное уравнение:

441 х 441 х 2 .

Р е ш е н и е . Введем новые переменные так, чтобы получились

симметрические многочлены. Обозначим 441 х у и 441 х z , тогда

у z 2 , кроме того, у4 z4 41 х 41 х 82. Таким образом,

получим систему уравнений:

у х 2,

у4 z 4 82.

Так как

у4 z4 ( у z)4 4( у z)2 уz 2( уz)2 ,

то

1		2,
	4	4	2		2	2	82.
	1		1	2		2

Подставим 1 2 во второе уравнение и получим:

			16 4 4			2		2 2			82 ,
						2				2
				2 2 16					2	0 ,
					2				2
			2		8		2	33 0 .
				2			2
		11	у z 2							или		у z 2			;
	2	3			11					или			уz 3		;
		3		уz	11								уz 3
	2
у и z являются	корнями квадратного										уравнения			t 2 2t 11 0		или
t 2 2t 3 0. Так как для уравнения									t 2 2t 11 0 ,					D 0 , то у и		z –

комплексные, а для иррациональных уравнений берутся действительные значения.

Решением уравнения		t 2		у 3		у 1	.
Решением уравнения		t 2	2t 3 0 являются		или		.
				z 1	z 3
Тогда:
4
4	41 х 3	41 х 81
	41 х 3	41 х 81
				решений нет ,
4	41 х 1		решений нет
	41 х 1
4
4	41 х 1	решений нет
	41 х 1	решений нет
			41 х 81	решений нет .
4	41 х 3		41 х 81
	41 х 3

У п р а ж н е н и я

1. Выразить многочлен через элементарные симметрические многочлены:

а) f (х1, х2 , х3 ) х15 х22 х12 х25 х15 х32 х12 х35 х25 х32 х22 х35 . б) f (х1, х2 , х3 ) х14 х24 х34 2х12 х22 2х22 х32 2х32 х12 .

в) f (х1, х2 , х3 ) (х1 х2 )(х1 х3 )(х2 х3 ) .

г) f (х1, х2 , х3 ) (х1х2 х3х4 )(х1х3 х2 х4 )(х1х4 х2 х3 ) .

д) f (х1, х2 , х3 ) (2х1 х2 х3 )(2х2 х1 х3 )(2х3 х1 х2 ) .

Замечание: в задачах 3 – 5 для определения высшего члена целесообразно использовать лемму о высшем члене произведения многочленов. Например, для

f (х1, х2 , х3 ) (2х1 х2 х3 )(2х2 х1 х3 )(2х3 х1 х2 )

высший член равен 2х1 ( х1) ( х1) 2х13 .

2. Вычислить значение многочлена от корней уравнения:

а) f (х1, х2 , х3 ) (х12 х1х2 х22 )(х22 х2 х3 х32 )(х32 х3 х1 х12 ) ,

3 2 .

х 6х 7х80

б) f (х1, х2 , х3 ) х13 х2 х1х23 х23 х3 х2 х33 х33 х1 х3 х13 ,

3 2 .

х х 4х10

в) f (х , х , х ) х3 х3

х3

5х х х

3 2

1 2 3

х 5х 4х70

г) f (х1, х2 , х3 ) (х1х2 х3 х4 )(х1х3 х2 х4 )(х1х4 х2 х3 ) ,

4 3 2

х х 2х 3х20.

д) Найти сумму кубов корней уравнения: х4 2х3 х2 5х 3 0 .

Замечание:

задаче 5

сумма кубов

является

х х х х

симметрическим многочленом

f (х1, х2 , х3 , х4 ) .

3. Составить квадратное уравнение, корнями которого являются:

а) квадраты корней уравнения х2 6х 10 0 .

б) являются кубы корней уравнения х2 5х 3 0 .

в) четвертые степени корней квадратного уравнения х2 х 3 0 .

г)

числа:

х1 х2 , х1

х3 , х2

х3 , где х1,

х2 ,

х3

–

корни уравнения

х3 3х2 6х 10 0 .

д)

числа:

(х

х )2 ,

(х

х )2 ,

(х

х )2 , где

х , х

–

корни

уравнения х3 5х2 4х 7 0 .

4. Решить системы уравнений:

а)

;

б)

;

в)

;

у 5

ху

г)

х3

3 2

;

д)

у 2 ху

ху х

5. Решить иррациональные уравнения:

а) 497 х 4х 5.

б) х 17 х2 х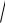17 х2 9 .

в) 310 х 33 х 1. г) 48 х 489 х 5 .

д) 3х 34 3х 3 1.

Глава II

РЕШЕНИЕ АЛГЕБРАИЧЕСКИХ УРАВНЕНИЙ В РАДИКАЛАХ

§ 1. Решение уравнений третьей степени в радикалах

По основной теореме Алгебры и следствию из нее, всякий многочлен

п-ой степени с произвольными комплексными коэффициентами имеет ровно п-комплексных корней.

Доказательство теоремы не дает практического способа нахождения корней. В этом параграфе мы рассмотрим, как находить комплексные корни некоторых многочленов. Нахождение корней многочлена будем связывать с решением уравнения

f (х) 0 . (*)

Определение. Решить уравнение (*) в радикалах – это значит,

выразить корни этого многочлена через его коэффициенты с помощью конечного числа операций: сложения, вычитания, умножения, деления,

возведения в степень и извлечения корня.

Рассмотрим следующие виды уравнений:

1) Пусть степень многочлена п 1. Тогда уравнение имеет вид:

а	0	х а	0 ,			а	0		0 х						а1	– решение в радикалах.
а		х а	0 ,			а			0 х							– решение в радикалах.
		1													а0
															а0
2) Пусть степень многочлена п 2. Тогда уравнение имеет вид:
						а х2 а х а 0 ,										а	0	0 ,
						0			1			2					0

				а				а2 4а		0	а	2
		х			1				1	0		2		– решение в радикалах.
		х												– решение в радикалах.
		1, 2					2а0
							2а0
3). Пусть степень многочлена п 3 . Тогда:
а х3		а х	2 а		2	х а			0,			а	0		0	– кубическое уравнение.
0		1			2		3						0

Способов решения такого уравнения в радикалах не имеем. Получим

формулы для решения квадратного уравнения, которые будут выражать корни данного уравнения через его коэффициенты. Поделим уравнение на

а0 :
х3	а1	х2	а2	х	а3	0 х3 ах2 bх с 0 .	(1)
	а0		а0		а0

Введем в рассмотрение				вспомогательную переменную			у , положив

х у , где R .

Итак: подставим

( у )3 а( у )2 b( у ) с 0.

у3 3у2 3у 2 3 ау2 2ау а 2 bу b с =0.

Запишем по убыванию степеней у :


у3	(3 а) у2 (3 2 2а b) у			3	а 2	b с	0 .

			р		q
Потребуем сами, чтобы коэффициент при					у2 был равен нулю, т. е.
3 а 0,		а	.
3 а 0,		3	.
		3
			у3 ру q 0 –				(2)

получили неполное кубическое уравнение.

Решив уравнение (2), мы решим наше исходное уравнение. Для решения уравнения (2), введем еще две вспомогательные переменные и и v , полагая у и v .

(и v)3 р(и v) q 0 ,

и3 3и2v 3иv2 v3 р(и v) q 0,

(и3 v3 ) 3иv(и v) р(и v) q 0 ,

(и3 v3 q) (и v) 3иv р 0.

Потребуем еще раз, чтобы 3иv р 0 , т. е.

и v	р	.	(**)
	3

Тогда уравнение примет вид:

у и v

и3 v3 q 0 ,

и3 v3 q .

Возведем (**) в третью степень:

и3 v3 р3 .

Приходим к системе уравнений:

	3	v	3	q
и		v		q

	3	v3			р	3
и	3				р
и
					27

и 3 и v3 являются корнями квадратного уравнения следующего вида:

				z и3					q					q2				р3			;
				z и3																	;
	р3			1				2					4 27
z2 qz	р3		0					2					4 27
z2 qz			0
27						v3				q				q	2			р	3
				z						q				q				р				;
				z	2																	;
					2			2					4					27
								2					4					27


у и v 3		q		q2			р3	3			q					q2				р3			.
у и v 3								3															.
2				4			27	2									4		27
Эта формула решения неполного кубического уравнения (2)
называется формулой Кардано.
При вычислении значений					и		и	v мы				получили три значения

кубического корня для и и три значения кубического корня для v . Значит,

для получится девять всевозможных комбинаций. Но

комбинировать можно не все и и v , а только те, которые удовлетворяют условию:


		и v			р		.		(**)
		и v					.		(**)
				3
Покажем, как выбрать все такие пары:									и и v . Предположим, что
одна такая пара есть: и	, v	, где и v				р		. Остальные пары и , v (их будет
одна такая пара есть: и	, v	, где и v						. Остальные пары и , v (их будет
1	1	1	1	3
				3

п ) мы найдем, используя значение кубического корня из 1.

Вычислим:

									0	1,
										0 2 k								0 2 k
3	1 3	1 соs 0 i sin 0			1					0 2 k					i sin			0 2 k				k 0, 1, 2 ;
									соs												,
									соs												,
											3									3

				cos		2		i sin			2			1		i	3		;
			1	cos				i sin								i			;
			1		3						3		2				2
					3						3		2				2

				cos			4		i sin			4			1	i	3			;
			2	cos					i sin							i				;
			2		3						3		2				2
					3						3		2				2

Напомним, что если известно одно значение корня n-ой степени из комплексного числа, то все n-значений этого корня можно получить умножением одного известного значения на значения корня: п1 .

В нашем случае, если известно и1 , то

									и1 и1 0 и1 ,

																			1									3

				и2 и1 1																		i									,
				и2 и1 1							и1								2			i					2				,
																			2								2

																			1									3

				и3 и1 2																		i
				и3 и1 2									и1						2			i					2			.
																			2								2
Аналогично:
									v1 v1 0 v1,

																			1									3
				v2 v1 1																		i									,

											v1								2								2
																			2								2

																			1									3

				v3 v1 2																		i
				v3 v1 2							v1								2			i					2			.
																			2								2
Мы предполагали, что и v																р		,			т.			е.				и			и		v		можно комбиниро-
Мы предполагали, что и v																		,			т.			е.				и	1		и		v		можно комбиниро-
									1		1				3														1					1
															3
вать для нахождения у . Покажем, что и2																					комбинируется с v3 , т. е.
									и		v									р		,
									и	2	v											,
										2	3								3
																			3

							1								3								1											3
								и1 i и1																		v1 iv1

	и2 v3						2								2								2											2
							2								2								2											2
																																				р
	1	и v			3	i и v						3		i и v									3		и v и v											р	.
		и v				i и v								i и v											и v и v												.
	4	1	1	4			1		1		4				1		1						4				1	1				1		1		3

Аналогично можно					показать,		что	произведение и							v			р	.
Аналогично можно					показать,		что	произведение и							v	2			.
														3		2	3
																	3
Получаем следующие три значения у :
у и v						;	х у		а			;
у и v						;	х у					;
1		1			1		1	1	3
									3
у		и			v	;	х у				а			;
у	2	и		2	v	;	х у							;
	2			2		2	2	2	3
									3
у и					v	;	х у			а			.
у и			3		v	;	х у						.
3			3		2		3	3	3
									3

Уравнение решено полностью.

Рассмотрим вопрос о том, какие корни имеет неполное кубическое

3	р, q R . Для этого
уравнение у руq 0, если коэффициенты его

обозначим выражение под знаком

2 3

q р D 4 27

–назовем дискриминантом неполного кубического уравнения.

1с л у ч а й . Пусть D 0 . Под знаками квадратных корней формулы Кардано стоят положительные числа, а под знаками кубических корней –

числа действительные. Но кубический корень из действительного числа имеет одно действительное значение и два комплексно-сопряженных.

Пусть и 1 – действительное значение радикала и , а v1 –

действительное значение радикала v . Отсюда следует, что у1 R . Найдем:

											и v					и v
			1		3		1		3
			1		3		1		3
у2	и2 v3	и1		i				i			1	1	i	3		1	1	С ,

			2		2	v1	2		2			2					2
			2		2		2		2			2					2
										и v					и v
			1		3		1		3
			1		3		1		3
										1		1			1		1
у3	и3 v2	и1		i				i					i	3				С .
у3	и3 v2	и1	2	i	2	v1	2	i	2			2	i	3			2	С .
			2		2		2		2			2					2

Итак: если D 0 , то неполное кубическое уравнение имеет один действительный корень и два комплексно-сопряженных.

2 с л у ч а й . D 0 . Тогда из формулы Кардано следует:


						и 3				q	;	v 3				q	.
						и 3					;	v 3					.
									2						2
		Пусть и1 –			действительное значение									радикала и, тогда, так как
и v			р	R , так как р R ,					v R ,			то можно сказать, что и v .
и v				R , так как р R ,					v R ,			то можно сказать, что и v .
1	1	3							1										1	1
		3					у1 и1 v1 2и1 R ,
							у1 и1 v1 2и1 R ,

								1			3		1					3

				у2 и2	v3				i						i				и1 R ,
				у2 и2	v3	и1		2	i		2	и1	2		i			2	и1 R ,
								2			2		2					2

								1			3		1					3

				у3 и3	v2				i						i				и1 R .
				у3 и3	v2	и1		2	i		2	и1	2		i			2	и1 R .
								2			2		2					2
		При		D 0 ,	все корни – действительные числа, причем два из них
равны.
		3 с л у ч а й . D 0 . Тогда под знаком квадратных корней формул

Кардано стоят отрицательные действительные числа. Квадратные корни из этих отрицательных действительных чисел – числа комплексносопряженные, и под знаком кубических корней тоже стоят комплексносопряженные числа. Так как уравнение имеет нечетную степень, то среди трех его комплексных корней должен быть хотя бы один действительный корень. Пусть это будет корень у1 и1 v1 R . Тогда корни у2 и у3 –

также действительные числа (проверить самостоятельно). Отсюда следует, что у2 , у3 R .

Итак, если D 0 , то неполное кубическое уравнение имеет три действительных корня, причем все они различны.

Хотя в случае (3) уравнение имеет три действительных корня, по формуле Кардано их найти часто сложно и даже невозможно. Связано это с тем, что мы приходим к извлечению кубического корня из комплексного числа, которое можно произвести только в тригонометрической форме. А это не всегда можно сделать точно. Поэтому случай (3) называют неприводимым случаем (не путать с неприводимостью многочлена). Отсюда следует, что практическое значение формул Кардано невелико.

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]