Исследование потока жидкости и газа при движении вблизи свободной поверхности тела (96

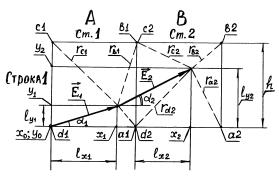
Delphi7. Распечатка такой программы приведена в приложении 1, а образец рабочего листа среды Excel с занесенными данными – в приложении 2.

Алгоритм построения линий напряженности по результатам измерений компонент вектора E поясняет рис. 8.

Рис. 8. Построение векторов напряженности в двух смежных ячейках проводящего листа

Для построения линий напряженности в виде цепочки последовательных векторов Ei , так или иначе привязанных к соответ-

ствующим ячейкам, используемый алгоритм требует перехода от размерных физических параметров (в первую очередь, линейныхG

размеров и соответствующих им координат, а также модулей Ei ) к

(см. формулы (28)). Численные значения базовых параметров h и E0 целесообразно принять равными единице, например в данной

работе h = 1 см, E0 =G1 В/см.

Первый вектор E1 j ( j = 1,2, …, 14 – номер строки, см. рис. 7)

как элемент линии напряженности строится по результатам измерения его компонент в данной ячейке.

22

переключателя, отслеживая возможность изменения знака вели-

где индекс i = 1 (ячейка 1-го столбца или столбца А в среде Excel);

где k = x, y, а расстояния от угловых точек a1, b1, c1, d1 данной ячейки до конца вектора E1, т. е. rai , rbi , rci , rdi , рассчитываются как

rai = (1−lxi )2 +lyi2 ;

rci = lxi 2 +(1−lyi )2 ;

rdi = lxi 2 +lyi 2 ,

где i = 1.

23

Для построения следующего вектора E3 используются форму-

гдеi = 3, 4, …

Исследуемый профиль имеет относительно небольшую толщину, и вихревые течения в потоке отсутствуют, поэтому изменение

направления векторов Ei относительно оси абсцисс выбранной

системы координат не происходит. Отметим также, что в случае частично недоступных ячеек считается возможным использовать зависимость (36) для продолжения построения линий напряженности величины rni (где n = a, b, c, d ), которые относятся к угловым

точкам ячейки, оказавшимся внутри выреза, эти точки следует полагать равными нулю. Некоторые из линий напряженности, стремящиеся по ходу их построения к вырезу, могут при очередном построении оказаться внутри выреза. Физически это означает, что данная линия находится в окрестности передней критической точки. Очевидно, что построение такой линии далее не ведется. С противоположной стороны выреза должна располагаться задняя критическая точка, положение которой оценивается при построении линий напряженности из узлов сетки за вырезом, относящихся к ячейкам, которые расположены наиболее близко к вырезу и является полностью доступными.

Эквипотенциальные линии строятся из точек bi ячеек строки 1 как линии, ортогональные к линиям напряженности.

2. Описание лабораторной установки

Принципиальная схема установки, приведенная на рис. 9, включает в себя следующие основные элементы: стабилизирован-

24

ный источник питания 1 (вид тока – постоянный), лабораторная модель 6 и регистрирующий прибор 8, в качестве которого предпочтительнее всего использовать мультиметр марки АМ-1109, работающий в режиме вольтметра постоянного тока.

Рис. 9. Схема экспериментальной установки:

1 – источник питания; 2 – левая проводящая шина; 3 – проводящий лист; 4 – вырез; 5 – правая проводящая шина; 6 – лабораторная модель; 7 – двойной зонд;

8 – регистрирующий прибор (мультиметр)

Модель 6, основой которой является диэлектрическая пластина, содержит плоский проводящий лист 3 из электропроводной бумаги с вырезом 4, имитирующим обтекаемое тело.

Проводящий лист 3 прижимается к диэлектрическому основанию двумя подводящими шинами 2 и 5, выполненными из алюминиевого сплава.

Шины крепятся на диэлектрическом основании винтами. При этом левая шина 2 соединена с положительной клеммой источника, а правая – с его отрицательной клеммой.

Двойной зонд 7 с расстоянием между иглами, которое равно шагу сетки, нанесенной карандашом на проводящий лист, соединен двумя проводами разных цветов с гнездами мультиметра 8.

Гнезда мультиметра 8 относятся к одному из двух его независимых измерительных каналов, другой его канал целесообразно использовать для контроля за выходным напряжением источника питания.

3. Порядок выполнения работы

Для записи экспериментальных данных необходимо иметь так называемый первичный лист формата А3 с нанесенной на него ко-

25

ординатной сеткой (шаг 1,5 см) и вырезом, условно имитирующим обтекаемое тело по образцу рис. 7.

Для проведения лабораторной работы необходимо выполнить следующее.

1.Проверить правильность сборки экспериментальной установки (см. рис. 9) и показать ее преподавателю или лаборанту.

2.Включить источник питания, включить мультиметр, переведя дисковые переключатели из положения «OFF» в положение

«=V» (см. рис. 9).

3.Установить иглы двойного зонда 7 (см. рис. 9) на точки a2 и d2 ячейки В2 (см. рис. 10) проводящего листа и зафиксировать зонд в вертикальном положении легким нажатием. Осторожно вращая регулятор источника питания, добиться разности потен-

циалов между иглами U0 =1±0,02 В, считывая показания муль-

тиметра 8 по одному каналу, тогда показания другого канала мультиметра при этой разности потенциалов будут соответствовать выходному напряжению источника, значение которого следует записать в отчет с точностью до десятых долей вольта. Если показания прибора оказываются отрицательными, необходимо поменять иглы зонда 7 местами. В любом случае нужно записать ту последовательность расположения игл зонда, которая обеспечивает положительные значения разности потенциалов вблизи левой подводящей шины. Далее следует перевести одну иглу зонда из точки a2 в точку с2 (см. рис. 10), оставив другую иглу зонда в прежней позиции (в точке d2). Показания мультиметра в этом случае должны упасть до сотых долей вольта. Осуществить данные манипуляции с зондом 7 (см. рис. 9) для ячеек В8 и В13 (см. рис. 7), убедившись, что и в этих ячейках сформировались такие же значения разностей потенциалов, как и в ячейке В2 (см. рис. 7, 10).

Рис. 10. Расположение игл двойного зонда (по горизонтали – угловые точки ячеек d, a; по вертикали – угловые точки ячеек d, с) при проведении измерений в поле проводящего листа

26

ВНИМАНИЕ! Во избежание повреждения проводящего листа недопустимо переводить иглы зонда из одного положения в другое при скольжении их концов по листу. Также нежелателен прямой контакт пальцев и ладоней с полем листа, поскольку при этом вытирается наполнитель листа (угольная пыль). Опираться пальцами или ладонью на проводящий лист можно только подложив под место такого контакта чистый лист обычной бумаги.

4.Провести систематические измерения, последовательно располагая иглы зонда в каждой ячейке (см. рис. 10) по горизонтали (точки d и a) и вертикали (точки d и с) с занесением результатов в первичный лист. С целью получения стабильных данных следует удерживать зонд плотно и равномерно прижатым к листу в течение 3–5 с.

5.Обработать полученные экспериментальные данные с помощью ПЭВМ, построив в соответствии с сеткой, изображенной на рис. 7, линии напряженности и линии эквипотенциальные.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.В чем состоит физический смысл уравнения неразрывности жидкости и газа?

2.Чем отличаются друг от друга линии тока и траектории частиц в потоке жидкости?

3.Какие точки на обтекаемом потоком теле называются критическими?

4.Как выглядит электрическое поле снаружи и внутри проводника с током? Где располагаются заряды, порождающие это поле?

5.Каким образом, располагая семейством линий напряженно-

сти и зная распределение модуля вектора E вдоль каждой линии, можно определить распределение избыточного давления по поверхности обтекаемого тела?

6.Что означают термины «математическое моделирование», «физическое моделирование», «критерий подобия»?

7.Какие факторы в данной лабораторной работе определяют погрешности измерений и построений? Каким образом можно количественно оценить влияние этих факторов?

27

ПРИЛОЖЕНИЕ 1

Рабочая программа (среда Delphi 7)

unit Main;

interface

uses

Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms, Dialogs, ExtCtrls, StdCtrls,math, ExtDlgs,comobj;

const h=1;

XCells=22;

YCells=15;

eps=0.0001; type

Knot= record X:double; Y:double; end;

TForm1 = class(TForm) Panel1: TPanel; Image1: TImage; Button2: TButton; Button3: TButton; Button4: TButton; DlgSave: TSaveDialog; DlgOpen: TOpenDialog; Button5: TButton; Button6: TButton;

SPD: TSavePictureDialog;

procedure FormCreate(Sender: TObject); procedure Button2Click(Sender: TObject); procedure Button3Click(Sender: TObject); procedure Button4Click(Sender: TObject); procedure Button5Click(Sender: TObject); procedure Button6Click(Sender: TObject); procedure Image1Click(Sender: TObject); public

XC,YC,RAD,Q:double; //Q - заряд на цилиндре в кулонах

28

Knots:array[1..XCells] of array[1..YCells] of Knot; //Напряжённость в единицах k-постоянной Больцмана

end; var

Form1: TForm1; cell:integer; implementation

{$R *.dfm}

//Профиль

procedure DrawObject; const a=15.25;

b=7.5; begin

with Form1.Image1.Canvas do begin

Arc(trunc(cell*5.2),cell*5,cell*11,cell*7,cell*11,cell*5,cell*5,cell*6);

Arc(trunc(cell*5.2),cell*4,cell*14,cell*8,cell*5,cell*6,trunc(cell*10.3),cell*8);

Arc(trunc(cell*9.8),trunc(cell*7.65),cell*22,trunc(cell*8.6),trunc(cell*11),trun

c(cell*7.6),0,trunc(cell*7.6));

MoveTo(trunc(cell*10.1),trunc(cell*5.28));

LineTo(trunc(cell*16.5),trunc(cell*8.5));

MoveTo(trunc(cell*12.2),trunc(cell*7.75));

LineTo(trunc(cell*16.35),trunc(cell*8.93));

Arc(trunc(cell*1+cell*a),trunc(cell*1+cell*b),trunc(cell*1.5+cell*a),trunc(cell

*1.5+cell*b),trunc(cell*1.0+cell*a),trunc(cell*1.5+cell*b),trunc(cell*1.25+cell

*a),trunc(cell*1+cell*b));

end;

end;

procedure TForm1.FormCreate(Sender: TObject); var i,j:integer;

begin

// Forb:=[]; DlgSave.InitialDir:=ExtractFileDir(Application.ExeName); DlgOpen.InitialDir:=ExtractFileDir(Application.ExeName);

cell:=Min((Image1.Width div (XCells+1)),(Image1.Width div (YCells+1))); DrawObject;

29

//Рисуем узлы i:=1;

j:=1;

while j<YCells do begin

Image1.Canvas.TextOut(15,cell*j+10,inttostr(j));

j:=j+1;

end;

while i<XCells do begin

j:=1;

Image1.Canvas.TextOut(cell*i+cell div 2,15,chr(i+64)); while j<=YCells do

begin Image1.Canvas.Ellipse(cell*i-1,cell*j-1,cell*i+1,cell*j+1); j:=j+1;

end;

i:=i+1;

end;

j:=1;

while j<YCells do begin

Image1.Canvas.Ellipse(cell*i-1,cell*j-1,cell*i+1,cell*j+1); j:=j+1;

end;

end;

//Тестовое поле

procedure TForm1.Button2Click(Sender: TObject); var r,a:double;

i,j:integer; begin

//Рассчитываем поле в узлах. //DrawObject;

i:=1;

j:=1;

while i<=XCells do begin

j:=1;

while j<=YCells do begin Knots[i][j].X:=10/cell;

30

Knots[i][j].Y:=-sign((Image1.Height div 2)-cell*j)*(round(((Image1.Width div 2)-cell*i)) div 50)/cell;

j:=j+1;

end;

i:=i+1;

end;

//Рисуем поле в узлах i:=1;

j:=1;

while i<=XCells do begin

j:=1;

while j<=YCells do begin

Image1.Canvas.MoveTo(round(cell*i),round(cell*j)); Image1.Canvas.LineTo(round(cell*(i+Knots[i][j].X)),round(cell*(j-

Knots[i][j].Y))); Image1.Canvas.Ellipse(round(cell*(i+Knots[i][j].X))-2,round(cell*(j-

Knots[i][j].Y))-2,round(cell*(i+Knots[i][j].X))+2,round(cell*(j- Knots[i][j].Y))+2);

j:=j+1;

end;

i:=i+1;

end;

end;

//Загрузка базисного поля из файла .xls procedure TForm1.Button3Click(Sender: TObject); var i,j:integer;

Excel:variant; begin

if DlgOpen.Execute then begin

i:=1;

Excel:=CreateOleObject('Excel.Application');

Excel.WorkBooks.Open(DlgOpen.FileName); while i<=YCells do

begin j:=1;

while j<=XCells do begin

31