
Исследование логических элементов (120
..pdfМосковский государственный технический университет имени Н. Э. Баумана
В. Н. Атаманов
ИССЛЕДОВАНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Методические указания к лабораторной работе № 42 по курсу «Электротехника и электроника»
Москва Издательство МГТУ им. Н. Э. Баумана
2011
УДК 621.3 ББК 31.2
А92
Рецензент А. А. Мальцев
Атаманов В. Н.
А92 Исследование логических элементов : метод. указания к лабораторной работе № 42 по курсу «Электротехника и электроника» / В. Н. Атаманов. — М. : Изд-во МГТУ им. Н. Э. Баумана, 2011. — 15, [1] с. : ил.
Знакомят с основными логическими элементами и их функциональными возможностями для построения сложных устройств.
Рассмотрены простейшие основные (базовые) логические элементы, реализующие логические функции на элементах комбинационного типа.
Для студентов 3-го и 4-го курсов факультета МТ. Рекомендовано Учебно-методической комиссией НУК ФН.
УДК 621.3 ББК 31.2
Учебное издание
Атаманов Валерий Николаевич
ИССЛЕДОВАНИЕ ЛОГИЧЕСКИХ ЭЛЕМЕНТОВ
Редактор В. М. Царев Корректор Л. С. Горбенко
Компьютерная верстка М. А. Голуба
Подписано в печать 11.01.2011. Усл. печ. л. 0,93. Формат 60×84/16. Тираж 800 экз. Изд. № 18. Заказ
Издательство МГТУ им. Н. Э. Баумана. Типография МГТУ им. Н. Э. Баумана. 105005, Москва, 2-я Бауманская ул., 5.
c МГТУ им. Н. Э. Баумана, 2011
Цель работы — ознакомление с основными логическими элементами и их функциональными возможностями для построения сложных логических устройств.
В процессе выполнения работы студенты изучают простейшие основные (базовые) логические элементы, реализующие логические функции на элементах комбинационного типа.
Теоретические сведения
Логические элементы
Логическими элементами называют электронные устройства, осуществляющие логические операции с цифровыми сигналами.
Существует ограниченное число простейших логических элементов, с помощью которых можно реализовать любую, в том числе самую сложную логическую функцию, например сложение, вычитание, сравнение цифровых сигналов. Даже такие сложные электронные устройства, как цифровые ЭВМ, могут быть созданы с помощью простейших логических элементов.
Техническое выполнение логических элементов может быть разным — на реле, транзисторах, диодах. В настоящее время используют в основном логические элементы в виде цифровых интегральных микросхем, составляющих основу импульсных электронных устройств.
Функциональные свойства логических элементов и устройств могут быть описаны таблицей истинности (табличная форма) или булевым уравнением (аналитическая форма).
Таблица истинности показывает состояние выхода логического элемента или логического устройства при всех возможных комбинациях сигналов на их входах. Таким образом, таблица истинности дает исчерпывающую характеристику работы логического элемента, т. е. описывает логическую функцию. Логическая функция, представленная символами алгебры Буля, выражается булевым уравнением.
На принципиальной схеме логический элемент изображают прямоугольником, внутри которого ставят символ указателя функции.
3

Линии с левой стороны прямоугольника показывают входы, с правой — выходы элемента. На рис. 1 показаны условные графические изображения, таблицы истинности и соответствующие им булевы выражения основных логических элементов, используемых в цифровых устройствах:
элемент И (конъюнктор, &), Y = A · B (рис. 1, а); элемент ИЛИ (дизъюнктор, 1), Y = A + B (рис. 1, б); элемент НЕ (инвертор, 1), Y = A (рис. 1, в);
элемент исключающее ИЛИ (сумматор по модулю 2, = 1), Y = A B (рис. 1, г).
Рис. 1. Условные графические изображения логических элементов:
а — конъюнктор; б — дизъюнктор; в — инвертор; г — элемент исключающее ИЛИ
Помимо указанных существует множество логических элементов, выполняющих более сложные логические преобразования. Эти преобразования являются комбинациями простейших логических операций. К числу таких элементов относят представленные на рис. 2:
элемент И—НЕ, Y = A · B (рис. 2, а); элемент ИЛИ—НЕ, Y = A + B (рис. 2, б);
элемент исключающее ИЛИ—НЕ, Y = A B (см. рис. 2, в). Набор логических элементов, способный осуществить все эле-
ментарные логические операции, представленные на рис. 1, называют функционально полным. Используя только один логический элемент И—НЕ, можно осуществлять все перечисленные элементарные логические операции. Таким образом, элемент И—НЕ носит универсальный характер и эквивалентен полному набору. Все логи-
4
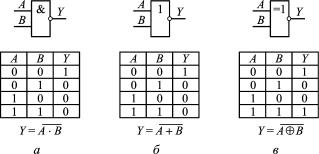
Рис. 2. Логические элементы:
а — элемент ИЛИ—НЕ; б — элемент И—НЕ; в — элемент исключающее ИЛИ—НЕ
ческие элементы, исследуемые в данной работе, выполнены на базе этого элемента.
Принцип построения принципиальной схемы комбинационного логического устройства
Комбинационное логическое устройство — это устройство, состояние выхода которого в данный момент времени определяется только комбинацией входных сигналов, т. е. не содержащее элементов в памяти.
Синтез принципиальных схем комбинационных логических устройств выполняют в такой последовательности:
—строят таблицу истинности логического устройства, которое осуществляет заданный закон его функционирования;
—записывают булево выражение, соответствующее построенной таблице истинности;
—упрощают его;
—составляют принципиальную схему логического устройства на основе упрощенного булева выражения.
В большинстве случаев конструирование логических схем начинают с составления таблицы истинности, которая показывает, каким должно быть состояние выхода при всех возможных комбинациях входных сигналов. Закон функционирования логического устройства, описываемый таблицей истинности, определяется требуемыми свойствами цифрового автомата. Необходимо уметь преобразовы-
5
вать информацию, представленную в форме таблицы истинности, в булево выражение.
Обратимся к таблице истинности, показанной на рис. 3. Заметим, что только две из восьми возможных комбинаций двоичных сигналов на выводах A, B и C дают на выходе логическую
A |
B |
C |
Y |
0 |
0 |
0 |
0 |
|
|
|
|
0 |
0 |
1 |
0 |
|
|
|
|
0 |
1 |
0 |
0 |
|
|
|
|
0 |
1 |
1 |
1 |
|
|
|
|
1 |
0 |
0 |
1 |
|
|
|
|
1 |
0 |
1 |
0 |
|
|
|
|
1 |
1 |
0 |
0 |
|
|
|
|
1 |
1 |
1 |
0 |
|
|
|
|
единицу. Эти две возможные комбинации представлены выражениями A · B · C и A · B · C. Таким образом, эти комбинации связываются логической функцией ИЛИ, чтобы получить булево выражение для данной таблицы истинности:
A · B · C + A · B · C = Y.
В общем случае при преобразовании таблицы истинности в булево выражение необходимо отыскать такие комбинации переменных, кото-
рые дают логические единицы, записать булево выражение комбинаций входных переменных и связать их операциями логического сложения. Полученное таким образом булево выражение функционирования логического устройства используют в качестве исходного для построения принципиальной схемы.
Логическое устройство, построенное на базе исходного булева выражения, не будет оптимальным с точки зрения количества используемых элементарных логических элементов. Синтез комбинационного логического устройства включает операцию минимизации исходного булева выражения. Минимизация булева выражения может быть достигнута при анализе таблицы истинности с помощью теорем булевой алгебры или на основе использования карт Карно. Наиболее предпочтительным является метод минимизации, базирующийся на использовании карт Карно. Прежде чем описывать структуру карт Карно, рассмотрим более подробно какую-ни- будь логическую функцию с ее таблицей истинности и исследуем следующую проблему: нельзя ли сделать упрощения, которые привели бы к уменьшению числа логических операций. Пусть дана функция Y (A, B, C, D) с соответствующей таблицей истинности (рис. 4). При этом A, B, C, D — переменные, про которые известно, что они входят в состав 16 групп, реализующих 16 различных комбинаций логических нулей и единиц.
6
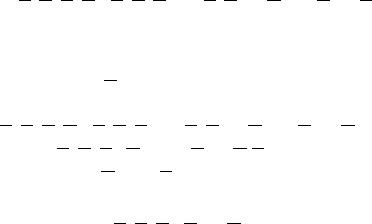
№ |
A |
B |
C |
D |
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
1 |
Y0 = A · B · C · D |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
0 |
0 |
0 |
1 |
1 |
Y1 = A · B · C · D |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
0 |
0 |
1 |
0 |
1 |
Y2 = A · B · C · D |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
3 |
0 |
0 |
1 |
1 |
0 |
Y3 = A · B · C · D |
|||||||||||
4 |
0 |
1 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
5 |
0 |
1 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
0 |
1 |
1 |
0 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
0 |
1 |
1 |
1 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
8 |
1 |
0 |
0 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
9 |
1 |
0 |
0 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
||||||||
10 |
1 |
0 |
1 |
0 |
1 |
Y10 = A · B · C · D |
|||||||||||
11 |
1 |
0 |
1 |
1 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
12 |
1 |
1 |
0 |
0 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
1 |
1 |
0 |
1 |
0 |
. |
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
||||||
14 |
1 |
1 |
1 |
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
15 |
1 |
1 |
1 |
1 |
0 |
Y15 = A · B · C · D |
|||||||||||
Рис. 4. Таблица истинности для минимизации булева выражения (жирным выделены несовпадающие значения в столбцах)
Допустим, что в разрабатываемой логической схеме использовано следующее соотношение булевой алгебры:
Y= Y0 + Y1 + Y2 + Y10 =
=A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D.
Из таблицы истинности (рис. 4) следует, что в членах Y0 и Y1 переменная D не оказывает влияния на состояние выхода логического элемента. То же наблюдается для членов Y2 и Y10, в которых
можно вычеркнуть A и A. Оба рассмотренных случая согласуются с результатами анализа в рамках булевой алгебры, так как
Y = A · B · C · D + A · B · C · D + A · B · C · D + A · B · C · D,
Y = A · B · C · (D + D) + B · C · D(A + A),
D + D = A + A = 1,
в результате чего получаем минимальную форму:
Y = A · B · C + B · C · D.
7
Отсюда видно, что упрощение логического выражения возможно при анализе таблицы истинности или на основе булевой алгебры. Аналогичная операция может быть выполнена еще проще при использовании карт Карно, т. е. графическим методом.
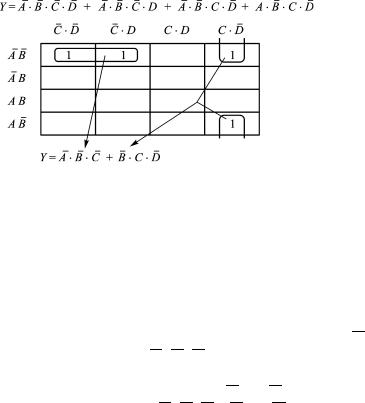
В общем случае число квадратов карт Карно равно числу возможных комбинаций переменных. Таблица истинности для четырех элементов включает 16 возможных комбинаций. Они представлены соответственно 16 квадратами карты (рис. 5).
Рис. 5. Карта Карно
Запишем в квадраты карты четыре единицы, соответствующие четырем членам в рассматриваемом примере (см. рис. 4).
Группы расположенных рядом единиц объединим контурами (см. рис. 5). В контуры объединяются единицы, находящиеся в периферийных квадратах карты, если оказываются рядом при сворачивании карты в цилиндр вокруг вертикальной или горизонтальной оси и если они расположены во всех четырех углах карты.
Левый контур (см. рис. 5) дает возможность вычеркнуть D и D, после чего в нем остается член A · B · C. В правом контуре, получаемом при сворачивании карты вокруг горизонтальной оси, можно вычеркнуть A, и тогда в нем остается член B · C · D. Упрощенное булево выражение имеет вид Y = A · B · C + B · C · D.
Для упрощения булевых выражений с двумя, тремя и четырьмя переменными применяют общую процедуру и одинаковые правила, и чем больше единиц объединяются в контуре, тем больше переменных можно опустить.
8
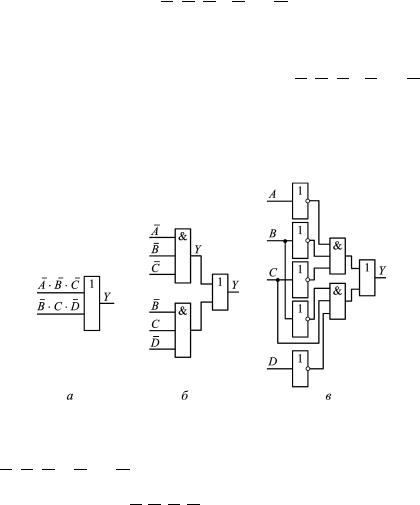
Следующим этапом синтеза комбинационного логического устройства является разработка его принципиальной схемы на базе минимизированного булева выражения.
Разработаем принципиальную схему логического устройства, реализующего булево выражение вида
Y = A · B · C + B · C · D.
На рис. 6 представлена последовательность построения схемы по шагам. Посмотрев на заданное выражение, легко заметить, что для получения нужного результата на выходе Y необходимо выполнить логическую операцию ИЛИ над членами A · B · C и B · C · D. На рис. 6, а показан первый шаг разработки принципиальной схемы логического устройства, т. е. как необходимый результат на выходе Y можно сформировать с помощью логического элемента ИЛИ с двумя входами.
Рис. 6. Последовательность построения схемы:
а — первый шаг; б — второй шаг; в — третий шаг
На втором шаге (рис. 6, б) для формирования комбинаций A · B · C и B · C · D на входах элемента ИЛИ добавлены элементы И. На третьем шаге (рис. 6, в) в схему вводят инверторы для получения значений A, B, C, D и объединяют входы элементарных логических элементов, на которые подается один и тот же входной сигнал.
9

Заметим, что начинают построение схемы с выхода и постепенно переходят ко входам.
Булевы выражения встречаются в двух основных формах. Одна из них — сумма произведений, другая — произведение сумм. Булево выражение в виде суммы произведений называют дизъюнктивной нормальной формой (ДНФ), построение принципиальной схемы начинают с логического элемента ИЛИ, число входов которого равно числу произведений. Булево выражение в виде произведения сумм называют конъюнктивной нормальной формой (КНФ), построение принципиальной схемы начинают с элемента И, число входов которого равно числу сумм.
Для проведения разных операций с переменными булевой алгебры требуется набор вычислительных правил:
A + 0 = A, |
A · 0 = 0, |
|||||||||||||||||||||||
A + 1 = 1, |
A · 1 = 1, |
|||||||||||||||||||||||
A + A = A, |
A · A = A, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A + A = 1, |
A · A = 0, |
|||||||||||||||||||||||
A + B = B + A, |
A · B = B · A, |
|||||||||||||||||||||||
A + B · C = (A + B) · (A + C), A · (B + C) = A · B + A · C, |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A + A · B = A, |
A · (A + B) = A · B, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A + A · B = A + B, |
A · (A + B) = A · B, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
A + A · B = A + B, |
A · (A + B) = A, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
A + A = A, |
A · A = A, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
A · B + A · B = A · B, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
A · B + A · B = A · B. |
||||||||||||||||
Теоремы де Моргана
1. Дополнение суммы равно произведению дополнений переменных:
A + B + C = A · B · C.
2. Дополнение произведения равно сумме дополнений переменных:
A · B · C = A + B + C.
10
