Математический анализ (Множества. Метод математической индукции) (110

Утверждено научно-методическим советом факультета компьютерных наук 26 апреля 2012 г., протокол № 5

Рецензент доктор физ.-мат. наук, профессор Воронежского государственного университета А.Д. Баев

Учебное пособие подготовлено на кафедре цифровых технологий факультета компьютерных наук Воронежского государственного университета.

Рекомендуется для студентов 1-го курса дневного отделения факультета компьютерных наук.

Для направлений 230400 – Информационные системы и технологии

2

3

Введение

Настоящее учебное пособие содержит два первых модуля курса математического анализа, включенного в ООП для направлений для направления «230400 – Информационные системы и технологии» на факультете компьютерных наук Воронежского государственного университета.

Оно будет полезным при проведении практических занятий и в процессе организации самостоятельной работы студентов.

Пособие содержит максимальное доступное изложение сложных вопросов. Пособие содержит разбор решений основных типовых задач по теории множеств и по методу математической индукции. Приводятся задачи для самостоятельного решения.

4

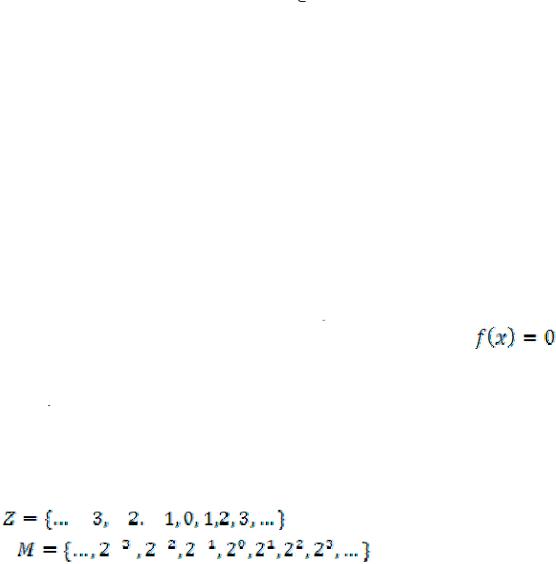
1.МНОЖЕСТВА

1.1.Способы задания множеств

Множества, как правило, обозначают прописными буквами некоторого алфавита - A, B, C, N. R… Элементы множества обычно обозначают строчными буквами - a, p, e, x, t… Знак обозначает принадлежность;

читается «элемент x принадлежит множеству M»; читается «элемент

x не принадлежит множеству M».

Буквами N, Z, Q, R обозначают, как правило, множества натуральных, целых, рациональных и действительных чисел соответственно.

Перечислим некоторые, наиболее употребляемые, способы задания множеств:

а) множество может быть задано путем перечисления всех его элементов; например, множество всех цифр {0, 1, 2, 3, 4, 5, 6, 7, 8, 9}; множество лиц, присутствующих в комнате {Коля, Володя, Ира, Лена, Оля}; множество всех трехзначных чисел в двоичной системе счисления {100, 101, 110, 111} и т.п.

b) Множество M может быть задано путем формулирования некоторого характеристического свойства P(x), которым обладают элементы множе-

ства (и только они одни): или.

можно составить следующим образом:

Е={x| }.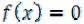

Множество А точек отрезка [0, 1] задается так: A={x: 0}.

c) Множество M может быть задано путем определения его элементов

Пустым называется множество, не содержащее никаких элементов. Оно обозначается символоми содержится в любом множестве.

Множества A и B называются равными, если они состоят из одних и тех же элементов.

Если каждый элемент множества A является элементом множества B, то говорят, что множество A содержится в множестве B (пишут )

или, что то же, множество B содержит множество A (пишут). В этих случаях говорят, что множество A является подмножеством множества B.

5

1.2. Операции над множествами

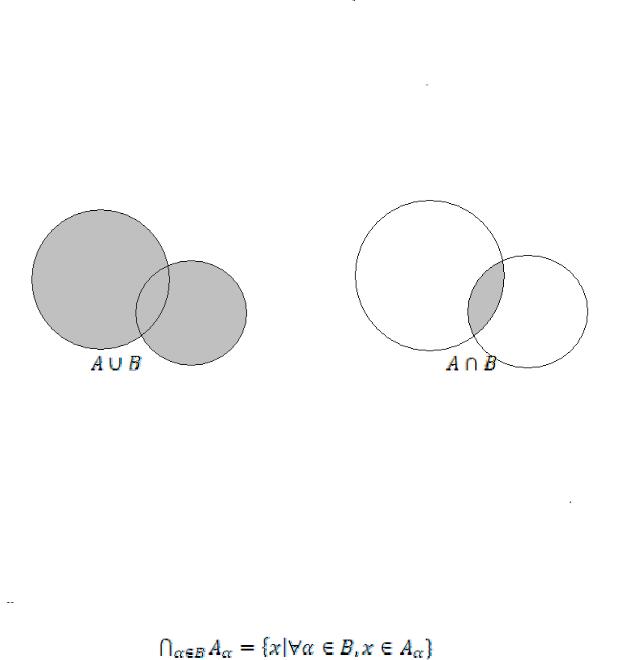
Пусть А и В - произвольные множества; их суммой или объединением 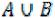называют множество, состоящее из всех элементов, принадлежащих

хотя бы одному из множеств А и В (см. рис. 1).

Аналогично определяется объединение любого (конечного или бесконечного) числа множеств. Пусть 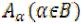- произвольные множества.

Объединением множеств называется множество тех элементов, каждый из которых принадлежит хотя бы одному из множеств, или

.

Очевидно, что для любого А выполняется.

Пересечением множеств А и В называется множество, состоящее из всех элементов, принадлежащих как А, так и В (см. рис. 2).

A A

B B

Рис. 1 Рис. 2 Например, пересечение множества всех четных чисел и множества

всех чисел, делящихся без остатка на три, состоит из всех целых чисел, делящихся без остатка на шесть.

Если множества С и D не имеют общих элементов, то . В этом случае множества С и D называются непересекающимися.

Полезно отметить, что.

Пересечением любого (конечного или бесконечного) числа множеств 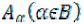называется множество элементов, принадлежащих каждому из

множеств, или

.

Разностью множеств А и В (обозначается А\В) называют множество, состоящее из тех элементов множества А, которые не принадлежат множе-

ству В (см. рис. 3). Ясно, что А\А=.

6

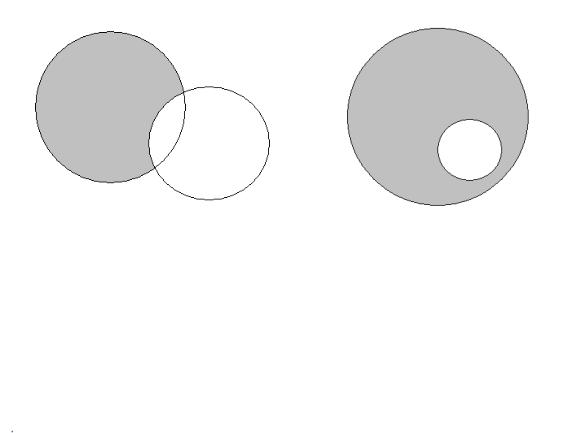
Если В, то А\В называют дополнением множества В до множест-

ва А (см. рис. 4).

Вслучае, когда рассматриваются различные подмножества множества

А(и только они одни), дополнение множества В до множества А называют просто дополнением.

Очевидно, что для любого множества А выполняется АА. Принято также считать, по определению, что пустое множество является подмножеством каждого множества: А. Для любого множества А само А и пустое множество называются его несобственными подмножествами. Если же А, и существует элемент x такой, что x не принадлежит А, то

А называется собственным подмножеством множества В.

Пример 1. Даны множества А, В и С. С помощью операций объединения и пересечения записать множество, состоящее из элементов, принадлежащих:

1) всем трем множествам; 2) хотя бы одному множеству; 3) по крайней мере двум этим множествам.

Решение. 1) (АВ) С;

2)(АВ) С;

3)(АВ) (СВ) (АС).

Пример 2. Найти АВ, АВ, А\В, В\А, если А={-4, -3, -2, -1, 0, 1}, B={-1, 0, 1, 2, 3}.

Решение. АВ={-4, -3, -2, -1, 0, 1, 2, 3}, АВ={-1, 0, 1}, А\В={-4, -3, -2}, В\А={2, 3}.

1.3. Эквивалентные множества

Говорят, что между множествами А и В установлено взаимно однозначное соответствие, если каждому элементу множества А сопоставлен

7

один и только один элемент множества В, так что различным элементам множества А сопоставлены различные элементы множества В и каждый элемент множества В оказывается сопоставленным некоторому элементу множества А.

Множества, между которыми можно установить взаимно однозначное соответствие, называют эквивалентными.

Если множества А и В эквивалентны, то пишут АВ.

Если А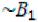, и В не эквивалентно А, то говорят, что множество А имеет меньшую мощность, чем множество В.

Множество А называется конечным, если существует такое число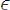 nN,

что А {1, 2, 3,…,n}.

В этом случае говорят, что множество А содержит n элементов или что множество А имеет мощность n.

Мощность пустого множества принимается равной нулю. Множество, не являющееся конечным, называется бесконечным.

Множество А называется счетным, если А N .

Множество называется несчетным, если оно имеет мощность, большую, чем мощность множества .

Теоремы Кантора.

1.Множество всех рациональных чисел счетно.

2.Множество всех действительных чисел несчетно.

Множество А называется множеством мощности континуума, если А.

Примеры с решениями

Пример 1. Даны множества A, B, C. С помощью операций объединения и пересечения запишем множества, состоящие из элементов, принадлежащих: 1) всем трем множествам; 2) хотя бы одному множеству; 3) по крайней мере двум этим множествам.

Решение. 1) (A ∩ B) ∩ C;

2)(A U B) U C;

3)(A ∩ B) U (C ∩ B) U (A ∩ C).

Пример 2. Найти А U В, А \ В, В \ А, А ∩ В, если

А={-4; -3; -2; -1; 0; 1}, В = {-1; 0; 1; 2; 3}.

Решение. А ∩ В = {-4; -3; -2; -1; 0; 1; 2; 3}; А ∩ В = {-1; 0; 1}; А \ В = {-4; -3; -2}; В \ А ={ 2; 3}.

Задачи для самостоятельного решения

Задача 1. Доказать, что включения А В и В А выполняются одновременно тогда и только тогда, когда А = В.

Задача 2. Докажите, что равенство А U В = В верно тогда и только тогда, когда A B.

8

Задача 3. Докажите, что равенство А ∩ В = А верно тогда и только тогда, когда A B.

Задача 4. Докажите, что (А \ В) ∩ (В \ А) = Ø.

Задача 5. Докажите, что любое непустое множество имеет не менее двух подмножеств.

Задача 6. Докажите, что если А В и В D, то A D.

Задача 7. Докажите, что если а А, то одноэлементное множество

{ а } А.

Задача 8. Докажите, что равенство A \ (В \ С) = (A \ B) U С верно тогда

и только тогда, когда А С.

Задача 9. Докажите равенство A \ (A \ B) = A ∩ B. Задача 10. Докажите, что А U (B U C) = (A U B) U C.

Задача 11. Докажите, что A ∩ (B U C) = (A ∩ B) U (A ∩ C). Задача 12. Докажите, что A ∩ (B U A) = A.

Задача 13. Докажите, что A U A = A.

Задача 14. Докажите, что A ∩ A = A.

Задача 15. Докажите, что (A \ B) U (B \ A) = (A U B) \ (A ∩ B). Задача 16. Докажите, что (A \ B) \ C = A \ (B U C).

Задача 17. Докажите, что (A \ B) ∩ C = (A ∩ C) \ (B ∩ C). Задача 18. Докажите, что A U (B \ C) (A U B) \ C. Задача 19. Докажите, что (A U C) \ B (A \ B) U C.

Задача 20. Докажите, что X \ ( αUB A α ) = αIB (X \ A α ).

Задача 21. Докажите, что X \ ( αIB A α ) = αUB (X \ A α ).

Задача 22. Найти А U В, А \ В, В \ А, А ∩ В, если

А = {- 1; 0; 1; 2; 3; 4; 5}, В = { 2; 3; 4; 5}.

Задача 23. Найти А UВ, А \ В, В \ А, А ∩ В, если

А = {- 1; 0; 1; 2; 3}, В = {- 2;- 1; 0; 1}.

1.4. Свойства действительных чисел

Операция сложения.

Для любых двух чисел a и b определено единственным способом число, называемое их суммой и обозначаемое a + b. Сумма обладает свойствами:

1.Для любых двух чисел a и b выполняется a + b= b + a. Это свойство называется переместительным (коммутативным) законом сложения.

2.Для любых трех чисел a, b, с выполняется a + (b + с)= (b + с)+а. Это свойство называется сочетательным (ассоциативным) законом сложения.

3.Существует число 0, называемое нулем, такое, что для любого числа a выполняется a + 0= a.

9

4. Для любого числа a существует число, обозначаемое -a и называемое противоположным данному, такое, что a +(- a)=0.

Далее вместо a +(- b) будем писать a - b.

Операция умножения.

Для любых двух чисел a и b определено единственным способом число, называемое их произведением и обозначаемое a b. Произведение обладает свойствами:

5. Для любых двух чисел a и b выполняется a b= b a. Это свойство называется переместительным (коммутативным) законом умножения.

6. Для любых трех чисел a, b, с выполняется a (b с)= (b с) а. Это

свойство называется сочетательным (ассоциативным) законом умножения. 7. Существует число 1, называемое единицей, такое, что для любого

числа a выполняется a 1= a.

8. Для любого a 0 существует число, обозначаемое и называе-

мое обратным данному, такое, что a =1.

Связь операции сложения и умножения.

9. Для любых трех чисел a, b, с выполняется a (b + с)= b а + с а.

Это свойство называется распределительным (дистрибутивным) законом умножения относительно сложения.

Упорядоченность.

Для любых двух чисел a и b определено одно из соотношений a < b (a меньше b), a = b (a равно b), a > b (a больше b) так, что выполняются свойства:

Свойство непрерывности.

12. Каковы бы ни были непустые множества у которых для любых элементов a A, b B выполняется неравенство a то существует такое число z, что для всех x A, y B выполняется

x.

1.5. Числовые промежутки

Отрезок, интервал, полуинтервал записываются соответственно как

[a,b]={x : a x b}, (a,b)={x : a x b}, [a,b)={x : a x < b}, (a,b]={x : a x b}.

Бесконечные промежутки записываются:

10