Автоматизированная обработка электроэнцефалограмм на ЭВМ (96

Московский государственный технический университет имени Н.Э. Баумана

П.В. Лужнов, И.К. Сергеев

АВТОМАТИЗИРОВАННАЯ ОБРАБОТКА ЭЛЕКТРОЭНЦЕФАЛОГРАММ НА ЭВМ

Методические указания к выполнению лабораторной работы по курсу «Методы обработки биосигналов»

М о с к в а Издательство МГТУ им. Н.Э. Баумана

2 0 0 6

УДК 681.30.2 ББК 53.4

Л82

Рецензент А.В. Самородов

Лужнов П.В., Сергеев И.К.

Л82 Автоматизированная обработка электроэнцефалограмм на ЭВМ: Методические указания к выполнению лабораторной работы по курсу «Методы обработки биосигналов». – М.: Изд-воМГТУим. Н.Э. Баумана, 2006. – 24 с.: ил.

ISBN 5-7038-2823-6

Даны практические рекомендации по изучению электроэнцефалографических сигналов. Рассмотрены вопросы генеза электроэнцефалограмм. Приведены современные методы оценки электроэнцефалографических сигналов с использованием спектральных методов и теории цифровой обработки сигналов.

Длястудентов4-гокурсафакультета«Биомедицинскаятехника». Ил. 8. Библиогр. 4 назв.

УДК 681.30.2 ББК 53.4

Петр Вячеславович Лужнов Игорь Константинович Сергеев

Автоматизированная обработка электроэнцефалограмм на ЭВМ

Редактор А.В. Сахарова Корректор М.А. Василевская

Компьютерная верстка А.Ю. Ураловой

Подписано в печать 28.03.2006. Формат 60 84/16 Бумага офсетная. Печ. л. 1,5. Усл. печ. л. 1,4. Уч.-изд. л. 1,3 Тираж 100 экз. Изд. № 20. Заказ

Издательство МГТУ им. Н.Э. Баумана 105005, Москва, 2-я Бауманская ул., 5

ВВЕДЕНИЕ

Аппараты и системы электрофизического воздействия на биоткани используют ответные реакции систем организма для задач терапии и диагностики. Количественно и качественно оценить такие реакции невозможно без адекватного метрологического обеспечения самого воздействия, т. е. без определения плотности токов, потоков мощности электрического поля в том или ином органе или ткани организма. Сложность физически корректного их описания обусловлена, во-первых, существенным различием удельных электрических сопротивлений биотканей и, во-вторых, неправильностью геометрической формы границ органов и тканей.

Эти проблемы затрудняют использование аналитических методов расчета токов в неоднородных биотканях, поэтому при расчете, как правило, приходится применять весьма трудоемкие и громоздкие численные методы. Однако независимо от выбранного в конечном итоге метода на начальном этапе решения реальных задач необходимо проводить их качественный анализ, который обычно основан на использовании известных аналитических решений подобных задач, а также на оценке их точности. Эту точность сопоставляют с точностью используемых методов измерения медикобиологических параметров ответных реакций живых систем на воздействие. Анализ погрешности большинства традиционных методов измерения параметров сердечно-сосудистой, дыхательной, костномышечной и других систем организма показывает, что она, как правило, не превышает 15…25 %. Повышение точности измерений затруднительно, так как интерпретация данных в параметрах состояния живых систем часто не позволяет осуществлять дифференцированную диагностику патологических процессов.

В данной работе рассмотрены задачи нахождения распределения токов в конечности человека при электростимуляции и при бесконтактном электромагнитном воздействии.

Цели работы – изучение методов формирования базовых моделей для расчета токов в неоднородных средах и исследование распределениялокальныхтоковвконечностиприбиоадекватныхвоздействиях.

3

ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Электростимуляция

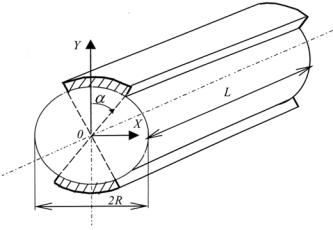
Для расчета параметров электростимуляции рассматриваем конечность (рис. 1), на поверхности которой установлены два длинных прямоугольных проводящих электрода, через которые протекает суммарный ток I. Хороший электрический контакт электродов с поверхностью кожи достигается при использовании, например, токопроводящих паст.

Рис. 1. Геометрические и биофизические параметры модели расчета плотностей токов при электростимуляции:

ρi – удельное электрическое сопротивление

Допускаем, что расположение кости в геометрическом центре конечности не является принципиальным. Обоснованность этого допущения в дальнейшем будет проанализирована.

Задачу распределения токов в такой системе можно разбить на следующие этапы [1]:

– нахождение распределения токов в однородно проводящем цилиндре с радиусом R без неоднородных включений, состоящем только из мягких тканей;

4

–учет влияния кости;

–учет влияния сосудов.

Выражение для комплексной плотности тока в однородно проводящей цилиндрической системе имеет вид (рис. 2) [2]

Рис. 2. Модель однородно проводящей цилиндрической системы

Проинтегрировав плотность тока в средней плоскости конечности, получим для оценки величины C1 общий ток

Из выражений (1) и (2) найдем следующие соотношения:

где k = sin α <1. Следовательно, в разложении (9) допустимо ог-

раничиваться конечным числом членов.

Окончательное выражение для константы С1 принимает вид

где

z =ρcos ϕ+iρsin ϕ,

7

Найденные соотношения позволяют определить значения плотности тока в любой точке цилиндра (см. рис. 2) и, следовательно, являются решением первого этапа задачи.

Вычислительный эксперимент, проведенный c использованием (11), показывает, что при учете реальных размеров конечности и кости плотность тока в пределах области расположения кости можно (с точностью до 10…15 %) считать постоянной по величине и направлению. Таким образом, в качестве модели для второго этапа решения задачи возможно рассматривать достаточно протяженную однородную среду проводимости γ3 с плотностью тока

j3 , в которую внесено цилиндрическое включение с проводимостями γ2 , γ1 (рис. 3).

Рис. 3. Модель для расчета распределения плотности тока в цилиндрическом включении

Расчеты надо проводить в центральной плоскости с тем, чтобы не учитывать эффектов конечной длины включения. В этом случае задача нахождения распределения электрического потенциала является плоской, а ее решение – решением уравнения Лапласа для распределения электрического потенциала, которое в полярных координатах имеет вид

8

Общее решение уравнения Лапласа в полярных координатах имеет вид

где константы определяются из граничных условий и особенностей рассматриваемой задачи. Для симметричной задачи в нашем

случае ϕ(−θ)=ϕ(θ) и, следовательно, в выражении (12) члены с sin (nθ) отсутствуют.

Плотности токов в биосредах определяются как j1 = E1 = γ1E1 = ρ1

= −γ1grad(ϕ1) [1, 4], а вследствие конечности потенциала при r = 0 из выражения (12) имеем

Учитывая, что решение должно иметь период 2π и принимая для внутренней области потенциал в центре равным нулю, получаем выражение для потенциала

Рассуждая аналогично, получаем следующие выражения для двух других областей решения:

j2 = E2 = γ2 E2 = −γ2grad(ϕ2 ), ρ2

При большом удалении от цилиндрического включения поле практически однородно, следовательно, должно выполняться ус-

На границах разделов r = a и r = b выполняются условия непрерывности потенциала и нормальных составляющих плотности тока. Нормальные компоненты плотности тока, как известно, определяются выражением

jni = −γi ∂ϕ∂ri .

Следовательно, имеем уравнения для нахождения оставшихся коэффициентов:

ϕ3 r=b =ϕ2 r=b A3b + Ab4 = E3b + Ab6 ,

10