
Математический анализ (числовые последовательности) (110
..pdf
ε > 0 n0 n ≥ n0 : xn −a ≥ ε;
или |
∞ |
, если существует такая окрестность точки a, вне которой |
|
находится бесконечно много членов последовательности |
. |
||
Последовательность называют расходящейся, если никакое число не является ее пределом, другими словами, если для любого числа a существу-
ет такое число ε > 0, что для любого натурального n0 найдется номер
n ≥ n0 такой, что xn −a ≥ ε, или
a ε > 0 n0 n ≥ n0 : xn −a ≥ ε.
6. Свойства сходящихся числовых последовательностей
1)Сходящаяся последовательность является ограниченной.
αсуществует∞
|
∞ |
|
и |
|
∞ |
|
∞ |
|
|
|
|
|
|
|
|
3) |
Если существуют |
|
∞ |
и |
|
∞ |
, то |
а) |
существует |
∞ |
· |
и |
|
; |
|
б) |
существует ∞ |
∞ |
и∞ |
· |
∞ |
||
|
∞ |
· |
∞ |
∞ |
; |
||
в) если к тому же для любого n выполнено то существует
.
0 и |
∞ |
0, |
4) |
Если |
⁄ |
∞ |
и |
∞ ⁄ |
, иlim |
|
⁄ lim |
|
. |
|
|
∞ |
|
|
∞ |
|
|
∞ |
|
∞ |
||
|
|
|
|
|
|
|
для всех n, начиная с неко- |
||||
торого, выполняется неравенство |
|
, то |
|
∞ |
. Это свой- |
||||||
ство называют леммой «о двух милиционерах». |
|
|
|
|
|||||||
5) |
Если |
|
∞ |
|
, и для всех n, начиная с некоторого, выпол- |
||||||
няется неравенство |
|
|
|
( или |
), то |
|
(или |
). |
|
|
|
6) |
Если |
|
∞ |
|
(или |
∞ |
|
), то для всех n, начиная |
|||
с некоторого, выполняется неравенство |
(или |
). |
|
|
|||||||
7. Бесконечно малые и бесконечно большие числовые последовательности
Сходящаяся последовательность, предел которой равен нулю, называ-
ется бесконечно малой.
Теорема. Для того, чтобы число а было пределом последовательности , необходимо и достаточно, чтобы для всех п
11

xn = a +αn ,
где |
-- бесконечно малая последовательность. |
|
|||||||
Последовательность |
|
|
|
называют бесконечно большой, если для ка- |
|||||
ждого |
ε > 0 существует |
такое натуральное число n0 , |
что для любого |
||||||
n ≥ n0 |
верно неравенство |
|
xn |
|
> ε, и в этом случае пишут |
|
|||
|
|
|
|||||||
|
|
|
|
|
|
∞ |
∞. |
|
|
Бесконечно |
большая |
последовательность |
имеет пределом ∞ |
||||||
(соответственно |
∞), если для каждого ε > 0 |
существует такое натураль- |
|||||||
ное число n0 , что для любого n ≥ n0 |
верно неравенство |
(соответст- |
|||||||
венно |
). Этот факт записывают так: |
|
|
||||||
|
|
∞ |
∞ (соответственно |
∞ |
∞). |
||||
Во всех рассмотренных случаях говорят, что последовательность име-
ет бесконечный предел.
Всякая бесконечно большая последовательность является неограни-
ченной. |
|
|
|
|
|
|
8. Частичный предел. Теорема Больцано – Вейерштрасса |
|
|||||
Если |
подпоследовательность |
последовательности |
имеет |
|||
конечный или бесконечный предел |
∞ |
, то а называют частич- |
||||
ным пределом последовательности |
|
|
|
|
||
Если |
∞ |
, где а конечный или бесконечный предел, то лю- |
||||
бая подпоследовательность |
последовательности |
имеет тот же |
||||
предел.
Теорема (Больцано – Вейерштрасса). Любая ограниченная последова-
тельность содержит сходящуюся подпоследовательность.
Всякая неограниченная последовательность имеет частичный предел ∞ или ∞. Таким образом, множество частичных пределов любой последовательности не пусто.
Пусть L – множество частичных пределов последовательности
(наряду с |
числами L может содержать и значения ∞ и ∞). |
Верхним |
|
(нижним) |
пределом последовательности |
называют sup L ( |
inf L ), и |
обозначают его ∞ ∞ .
Верхний и нижний пределы последовательности являются ее частичными пределами.
12

9. Фундаментальные последовательности. Критерий Коши
Последовательность называют фундаментальной, если для каждого ε > 0 существует такое натуральное n0 , что для любых натуральных
n, m ≥ n0 , верно неравенство xn − xm <ε.
Используя логические символы данное определение можно записать в
виде
ε >0 n0 N n, m N n, m ≥ n0 : xn − xm <ε.
Сформулированное утверждение называют условием Коши. Это же условие можно сформулировать и так: для каждого ε > 0 существует такое нату-
ральное n0 , что для любого натурального n ≥n0 и любого натурального р
верно неравенство xn+p − xn < ε.
В символической записи определение выглядит так
ε >0 n0 N n N n ≥n0 p N : xn+p −xn <ε.
Теорема (критерий Коши). Для того, чтобы последовательность имела конечный предел, необходимо и достаточно, чтобы она была фундаментальной.
Для того, чтобы последовательность не имела конечного предела, необходимо и достаточно, чтобы она не удовлетворяла условию Коши, т.е. удовлетворяла отрицанию условия Коши: существует такое ε >0 , что для
любого натурального n0 найдутся такие натуральные n, m ≥ n0 , что
xn − xm ≥ ε, или в символической записи:
ε > 0 n0 N n, m N n, m ≥ n0 : xn − xm ≥ε.
Примеры с решениями
Пример 1. Используя определение предела числовой последовательно-
сти, доказать, что число 1 является пределом последовательности |
, где |
|||||||||||||||||
xn = n /(n +1) |
(n =1, 2, 3,K). |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
xn −1 |
|
|
|
n |
|
|
|
|
|
1 |
|
|
||||
Решение. Рассмотрим модуль разности |
|
|
= |
|
|
|
−1 |
= |
. |
|||||||||
|
|
|
|
|
|
|||||||||||||
n |
+1 |
n +1 |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||
Возьмем произвольное число ε>0 . Неравенство |
|
|
xn −1 |
|
< ε будет вы- |
|||||||||||||
|
|
|
||||||||||||||||
полнено, если |
1 /(n +1) < ε , т.е. при n >1/ ε −1. Пусть A натуральное число, |
|||||||||||||||||
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
удовлетворяющее условию |
A >1/ ε−1, |
тогда 1/(A +1)< ε и для всех |
||||||||||
n ≥ A выполнены неравенства |
|
1 |
|
|
1 |
|
|
|||||
|
xn |
−1 |
|
= |
|
|
≤ |
|
< ε. |
|||
|
|
|
|
|||||||||
n |
+1 |
A +1 |
||||||||||
|
|
|
|
|
|
|
||||||
Это и означает, что предел рассматриваемой последовательности равен 1. Пример 2. Используя определение предела числовой последовательно-
сти, доказать, что |
∞ |
1 n3 |
0. |
|
|
|
|
|||
Решение. Так как 3 |
> n для любого n N , то |
|||||||||
Пусть ε > 0, |
|
|
(1/ 3)n −0 |
|
|
|
=1/ 3n <1/ n . |
|||
|
|
|
||||||||
выберем натуральное A такое, что 1/ A <ε. Тогда для |
||||||||||
любого n ≥ A имеем |
|
|
|
(1/ 3)n −0 |
|
|
||||
|
|
|
|
|
|
|
<1/ n ≤1/ A < ε . |
|||
|
|
|
|
|
|
|||||
Значит, ∞ |
1 3 |
|
0. |
|
|
|
|
|||
Пример 3. Используя определение предела числовой последовательно-
сти, доказать, что последовательность {(−1)n +1/ n }расходится. Решение. Нужно доказать, что никакое число не является пределом
данной последовательности.
Рассмотрим любые два соседних члена последовательности. Из этих |
||||||||||||||
членов один имеет четный номер n = 2 k , и x2k =1 +1/(2k ) |
>1. |
|||||||||||||
Соседний член имеет нечетный номер 2k +1 (или 2k −1 ), и |
||||||||||||||
x2k +1 |
= −1 + |
1 |
|
< 0 |
(или x2k −1 = −1 |
+ |
1 |
|
≤ 0 ). |
|||||
2k +1 |
2k −1 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||
Очевидно, |
что |
|
xn − xn+1 |
|
>1 . |
Следовательно, |
данная последователь- |
|||||||
|
|
|||||||||||||
ность не удовлетворяет условию Коши. |
|
|
|
|
||||||||||
Пример 4. Доказать, что последовательность {(n2 −10)/ n }расходится. Решение. Докажем, что данная последовательность не ограничена.
Имеем
xn = n −10 / n ≥ n −10 .
Пусть С – произвольное положительное число. Возьмем какое-нибудь натуральное число n0 >C +10 , тогда xn0 ≥ n0 −10 > C . Это означает, что
последовательность {(n2 −10)/ n }не ограничена, и поэтому расходится.
14
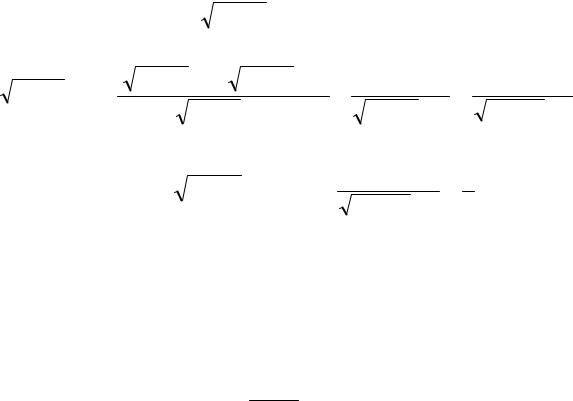
5n3 −3n2
Пример 5. Найти ∞ n3 +1 .
Решение. Преобразуем формулу общего члена последовательности:
|
|
x |
n |
= |
|
5 −3 / n |
. |
|
|
|
|
||
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
1 +1/ n3 |
|
|
|
|||||
Учитывая, что {1/ n}и {1/ n3 }– бесконечно малые последовательно- |
|||||||||||||
сти, и используя теоремы о пределах, получаем |
|
|
|
||||||||||
lim |
5 −3 / n |
|
|
= |
|
|
lim(5 −3 / n) |
= |
5 |
= 5. |
|||
|
|
|
|
|
n→∞ |
|
|
||||||
1 +1/ n3 |
|
|
|
|
lim(1 +1/ n3 ) |
1 |
|||||||
n→∞ |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
n→∞ |
|
|
|
||
Пример 6. Доказать, что |
|
|
(5n / nn )= 0 . |
|
|
|
|||||||
Решение. Для |
всех n ≥15 |
верно неравенство |
5 / n ≤1/ 3, поэтому |
||||||||||
0 < (5 / n)n ≤ (1/ 3)n |
при |
n ≥15 . |
Здесь слева и справа стоят члены беско- |
||||||||||
нечно малых последовательностей. Значит, по лемме «о двух милиционерах»
|
(5 n / n n )= 0 . |
Пример 7. Найти |
( n2 +n −n). |
Решение. Преобразуем формулу общего члена последовательности:
n |
2 |
+ n −n = |
( n2 + n −n)( n2 + n + n) |
= |
n |
|
= |
1 |
|
|
n2 + n + n |
n2 + n + n |
1 +1/ n +1 . |
||||||
Поскольку |
(1/ n)= 0 , то |
|
|
|
|
|
|
||
|
|
|
( n2 +n −n) = |
|
1 |
= |
1 . |
|
|
Пример 8. Для последовательности |
1 +1/ n +1 |
|
|
2 |
|
||||
|
|
|
|
|
|
||||
|
|
|
xn = (3cos (πn / 2)−1 )n +1 |
, n N, |
|
|
|
||
|
|
|
n |
|
|
|
|
|
|
найти |
множество частичных пределов, ее верхний и нижний пределы, а |
также |
и inf {xn }. |
Решение. При n = 4k имеем
xn = 2nn+1 = 2 + 1n ,
15
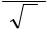
и, значит, |
x4k = 2, |
2 < x4k |
≤ 2 +1/ 4 , причем x4 |
= 9 / 4 . |
|||||||||||||
При n = 4k +1 или n = 4k +3 |
имеем |
|
|
||||||||||||||
|
|
|
xn |
= |
|
−n +1 |
= −1+ |
1 , |
|
||||||||
|
|
|
|
|
n |
|
|
|
|
||||||||
|
−1 < xn |
< 0, |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
и, значит, |
|
|
|
|
|
|
|
∞ 4 |
1 |
|
∞ 4 3 |
1. |
|||||
При n = 4k +2 имеем |
|
|
|
|
−4n +1 |
|
|
1 , |
|
||||||||
|
|
|
xn |
= |
|
|
= −4 + |
|
|||||||||
|
|
|
|
|
|
||||||||||||
значит, − 4 < xn < 0, |
|
|
|
|
|
|
|
|
n |
|
|
|
|
n |
|
||
|
|
|
|
|
|
|
∞ 4 |
2 |
|
4. |
|
|
|||||
Таким образом, числа 2, -1, -4 являются частичными пределами данной |
|||||||||||||||||
последовательности. |
Рассмотренные четыре подпоследовательности |
||||||||||||||||
тельность4 , 4. Отсюда1 , 4 |
следует2 , 4 |
, что3 |
составляют вместе всю данную последова- |
||||||||||||||
|
других частичных пределов последователь- |
||||||||||||||||
ность не имеет. |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
4 |
|
|
|
Очевидно, |
|
|
|
|
|
|
|
|
|
|
|
|
Из предыдущих рассмотре- |
||||
ний следует также, что∞ |
|
|
|
, |
|
|
|
|
|
∞4 |
9 4,inf. {xn }= −4 . |
||||||
|
|
|
|
|
|
|
|
||||||||||
Задачи для самостоятельного решения
Задача 1. Доказать, что следующие последовательности являются бесконечно малыми:
1) |
xn =1/ n; 2) |
xn |
= a / n , где a R; 3) |
xn |
= |
|
(−1)n+1 |
; |
|
|
|
|
|||||||||||||
|
n |
|
|
|
|
|
|||||||||||||||||||
|
xn = 2 +(−1)n ; |
|
|
1+(−1)n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
5) |
xn = |
; 6) |
|
xn = |
1 sin |
πn . |
|
|
|
|||||||||||||||
|
n |
|
|
|
|||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
n |
2 |
|
|
|
|
|
|||||
Задача 2. Доказать, что: |
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
3 |
|
||||||||
1) |
|
n +b |
=1, |
где b R; 2) |
|
|
n |
|
= |
1 |
; 3) |
|
|
= |
; |
||||||||||
∞ n |
|
|
|
|
|
|
2 |
||||||||||||||||||
∞ 2n +1 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
∞ 2n −1 |
|
|
||||||||||||||
4) |
|
2 |
− n |
= −1; |
5) |
n2 +2 |
1 =1; |
6) |
|
|
|
|
1 |
|
= 0 , где p ≥1. |
|
|||||||||
∞ 2 |
+ n |
|
|
|
|
p |
|
|
|||||||||||||||||
|
|
|
|
∞ |
n |
|
|
|
|
∞ n |
|
|
|
|
|
|
|
|
|
||||||
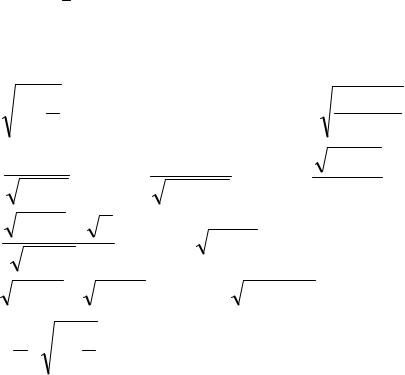
Задача 3. Доказать, что следующие последовательности являются бесконечно малыми:
n2 −1 ; |
|
|
2n +3 |
|
qn |
, |
|
q |
|
≤1; |
|
|
2n +1 |
|
sin n . |
||||
|
|
|
|
||||||||||||||||
|
|
|
; |
|
|
|
|
|
|
; |
|||||||||
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1) |
|
|
2) |
|
|
3) n3 |
|
|
|
|
4) |
|
|
5) |
|
||||
n |
|
|
|
n2 |
|
16 |
|
|
|
|
(n +1)2n |
n |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 4. Доказать, что следующие последовательности являются расходящимися:
|
|
|
|
}; 2) |
{n}; |
|
|
|
|
πn |
|
|
{sin n}; |
|
|
|
n |
|
|
2 |
πn |
|||||||
|
(− |
)n |
|
sin |
2 |
; |
4) |
5) |
|
|
|
|
cos |
|
3 |
. |
||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||
1) { |
|
1 |
|
|
3) |
|
|
|
|
|
|
n +1 |
|
|
|
|
||||||||||||
Задача 5. Найти пределы следующих последовательностей: |
|
|
||||||||||||||||||||||||||
|
|
|
|
1 n |
|
|
|
|
|
|
4 n+3 |
|
x |
|
|
|
n |
|
n |
|
|
|
||||||
1) |
x |
n |
= 1− |
|
|
; |
2) |
x |
n |
= 1+ |
|
; |
3) |
n |
= |
|
|
|
; |
|
|
|||||||
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
3n |
|
|
|
|
n |
|
|
n +5 |
|
|
|
|
||||||||||||||
4) |
xn |
= n[ln(n +3) −ln n]; 5) |
xn = n[ln n −ln(n + 2)]; |
|
|
|
|
|||||||||||||||||||||
n
6)xn = n −3 2
n
Задача 6. Найти пределы следующих последовательностей:
|
x |
|
= |
9 + |
|
1 ; |
|
|
x |
|
= |
|
8 − |
1 |
−1/ 3 |
; |
|
|
|
|
3 n |
+ |
0,25 |
|
||||
1) |
|
|
2) |
|
|
|
|
|
3) |
x |
|
= |
|
; |
||||||||||||||
|
|
|
n2 |
|
|
|
|
|
||||||||||||||||||||
|
n |
|
|
|
|
n |
n |
|
|
|
|
|
|
|
|
n |
|
8n +1 |
|
|||||||||
4) |
xn = n +1 |
1 |
; |
5) xn = n +1 |
; |
|
6) xn = 3 n2 + n |
; |
|
|||||||||||||||||||
|
|
|
|
n2 + |
|
|
|
|
|
|
n2 + 2n |
|
|
|
|
|
n + 2 |
|
|
|||||||||
7) |
xn = |
n2 |
|
+1 + |
|
n |
; |
8) |
x = n2 −1 −n −1; |
|
|
|
|
|
||||||||||||||
|
|
|
3 n3 |
|
+ n + n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
9) |
xn |
= |
n2 +n − |
|
n2 −n; 10) xn |
= 3 |
n3 +2n2 |
−n; |
|
|
|
|||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11) xn = |
|
|
|
1+ |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
3 |
n |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 7. Найти пределы следующих последовательностей:
1) |
xn = |
9 + n /(n +1) |
; |
2) xn = |
|
|
3 +0,5n |
|
|
; |
3) xn = |
|
n |
|
|
; |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
0,3 |
n+1 |
+5 |
|
|
|
|
|
|||||||||||||||||||||||||
|
2 +1/ n |
|
3n + 2 |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 −n |
|
|
n 2 |
−n |
|
|
|
|
|
|
|
|
n −1 |
|
5 |
|
|
|
|
3 |
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
4) |
xn = |
+ |
|
|
|
; 5) xn |
|
= |
|
|
|
|
|
; |
6) xn |
= |
n |
+ 27 |
; |
||||||||||||||||||||
|
|
|
|
|
n |
||||||||||||||||||||||||||||||||||
n +1 |
n +2 |
|
|
4 |
−15 |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|||||||||||||||||
7) |
xn = |
|
(n +5)3 −n (n +7)2 |
|
; |
|
8) |
|
xn = |
n2 +1 |
|
− |
3n2 +1; |
|
|||||||||||||||||||||||||
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
2n +1 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6n +1 |
|
|
||||||||||||
9) |
xn = |
|
(−1)n +1/ n |
|
; |
10) |
x |
|
|
= |
|
|
|
3n |
|
|
; |
|
|
|
|
|
|
|
|
|
|
||||||||||||
1/ n |
2 |
− |
|
n |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
5 +3 |
n+1 |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
(−1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
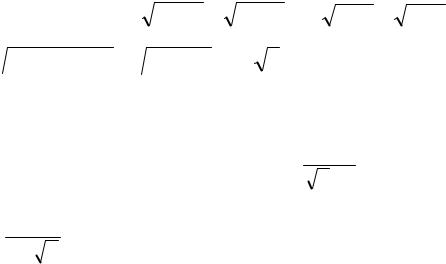
11) |
x |
|
= |
1+2 +K+n |
− n |
; |
12) |
x = |
2n+2 +3n+3 |
; |
||
n |
|
|
n +2 |
|
2 |
|
n |
2n +3n |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
13) |
x |
n |
= |
|
5 2n −3 5n+1 |
. |
|
|
|
|
|
|
100 2n +2 |
5n |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|||||
Задача 8. Найти пределы следующих последовательностей, если фор-
мула общего члена последовательности имеет вид: |
|||||||||||
|
(n +1)4 −(n −1)4 |
; 2) |
(n2 +3n + 4)3 −(n2 +3n −4)3 |
||||||||
1) |
|
|
|
|
; |
||||||
(n2 +1)2 −(n2 −1)2 |
|||||||||||
(n2 +5n +6)3 −(n2 +5n −6)3 |
|||||||||||
3) |
n2 |
|
− |
|
n3 |
; 4) |
n2 +1 − n2 −1; 5) 3 n +1 −3 n −1; |
||||
n +1 |
n |
2 |
+1 |
||||||||
6)  (n +2)(n +1)−
(n +2)(n +1)− n (n −1); 7) 3n 8.
n (n −1); 7) 3n 8.
Задача 9. Доказать, что следующие последовательности являются бесконечно большими:
|
|
n |
n |
|
n2 |
|
|
n |
! |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
; |
|
|
|
1 |
; |
|||||||||||
1) |
|
|
|
|
; |
2) |
|
|
|
3) |
|
|
|
; |
4) |
|||||||||
|
|
n +8 |
|
|||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||
|
10 |
|
|
|
4n |
n |
2 |
− |
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|||||
|
|
2 |
|
|
5n |
|
|
n |
|
|
|
a |
|
>1, |
|
k N. |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
5) |
|
|
n |
; 6) |
|
2 ; |
7) |
ak |
, где |
|
|
|||||||||||||
|
1− |
|
|
n |
|
n |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Задача10. Найтивсечастичныепределыследующихпоследовательностей:
|
(−1)n |
|
n2 |
|
1−n3 |
4) {(−1)n }; |
|||||||
1) |
n +1 |
; |
2) |
|
|
; |
3) |
1 |
+n2 |
; |
|||
n +5 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
π n |
|
|
|
π n |
|
||
|
n |
|
sin |
; |
|
n cos |
|
|
. |
||||
5) {3(−1) n }; 6) |
|
|
|
4 |
7) |
|
|
2 |
|
||||
Задача 11. Найти верхние и нижние пределы последовательностей:
|
|
πn |
|
|
|
|
|
n 2n + |
1 |
|
|
|
|
|
|
|
2 |
πn |
|
n |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
cos |
|
; |
|
|
|
(−1) |
|
|
|
|
; |
|
|
1,5cos |
|
|
|
|
|
|
|
; |
|
|
|
|
|||||||||||
1) |
|
3 |
|
|
2) |
|
|
|
|
n |
|
|
3) |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
{xn } |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
4) |
= |
1, |
1 |
, |
2 |
,K, |
9 |
, |
1 |
|
, |
|
|
2 |
|
,K, |
|
99 |
, K, |
|
|
1 |
|
, |
|
|
2 |
|
|
, K, |
10n −1 |
, K . |
||||||
|
|
|
|
2 |
|
|
|
2 |
|
|
2 |
|
|
|
n |
|
|
|
n |
|
n |
|||||||||||||||||
|
|
|
10 |
|
10 |
10 |
10 |
|
10 |
|
10 |
|
|
10 |
|
10 |
|
10 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
18

Варианты заданий, предлагавшихся на рубежных аттестациях
Вариант № 1 Задание 1. Сформулируйте и докажите теорему Больцано – Вейерштрасса о
существовании сходящейся подпоследовательности у ограниченной числовой последовательности.
Задание 2. Сформулируйте и докажите лемму «о двух милиционерах». Задание 3. Дайте определение ограниченной сверху последовательности.
Приведите примеры.
Задание 4. Дайте определение сходящейся последовательности. Приведите
|
примеры. |
|
Задание 5. |
Пусть последовательность {xn } сходится и ее предел a > 0 . |
|
|
Можно ли из {xn } выделить подпоследовательность, все члены |
|
|
которой отрицательны? |
{xn }, из |
Задание 6. |
Пусть x0 ≠ y0 . Постройте такую последовательность |
|
|
которой можно выделить две подпоследовательности |
{xn } и |
|
{xn }, одна из которых сходится к x0 , а вторая к y0 . |
m |
|
|
|
|
k |
|
Задание 7. |
Будет ли последовательность {xn }, где xn =3sin 4n, n N , ог- |
|
раниченной?
2n
Задание 8. Докажите, что ∞ n +1 =2.
Вариант № 2 Задание 1. Сформулируйте и докажите теорему о существовании предела у
монотонно возрастающей, ограниченной сверху последовательности.
Задание 2. Сформулируйте и докажите теорему об ограниченности сходящейся последовательности.
Задание 3. Дайте определение ограниченной последовательности. Приведите примеры.
Задание 4. Дайте определение неубывающей последовательности. Приведите примеры.
Задание 5. Пусть в некоторой окрестности точки a лежит бесконечно много членов последовательности {xn }. Следует ли отсюда, что никакая точка вне этой окрестности не является пределом последова-
тельности {xn }?
Задание 6. Покажите, что из любой неограниченной последовательности можно выделить бесконечно большую подпоследовательность.
19
Задание 7. Будет ли последовательность {xn }, где |
xn = (−1)n 3n2 +1 |
, n N, |
||
ограниченной? |
n |
|
||
|
|
|||
|
2n |
|
|
|
Задание 8. Докажите, что ∞ |
|
=0. |
|
|
n2 +1 |
|
|
||
Вариант № 3 Задание 1. Сформулируйте и докажите теорему о существовании предела у
монотонно убывающей, ограниченной снизу последовательности.
Задание 2. Сформулируйте и докажите свойства пределов числовых последовательностей.
Задание 3. Дайте определение верхнего предела числовой последовательности. Приведите примеры.
Задание 4. Дайте определение монотонно возрастающей последовательности. Приведите примеры.
Задание 5. Пусть последовательность {| xn |} сходится. Будет ли из этого вытекать, что последовательность {xn }будет сходящейся?
Задание 6. Пусть последовательность {xn } сходится, а последовательность {yn } расходится. Докажите, что сумма этих последовательностей {xn + yn } расходится.
Задание 7. Будет ли последовательность {xn }, где xn = n cos( π2n), n N,
ограниченной?
cos n
Задание 8. Докажите, что ∞ n2 +1 =0.
Вариант № 4 Задание 1. Сформулируйте и докажите теорему Больцано – Вейерштрасса о
существовании сходящейся подпоследовательности у ограниченной числовой последовательности.
Задание 2. Сформулируйте и докажите теорему о единственности предела числовой последовательности.
Задание 3. Дайте определение ограниченной снизу последовательности. Приведите примеры.
Задание 4. Дайте определение бесконечно большой последовательности. Приведите примеры.
20
