Линейные регрессионные модели (96

Используя формулу (7) для определения Sост2 , получаем искомую точечную оценку

Se2 = 5 1−1 (0,103 −0,1)2 + (0,183 −0,2)2 + (0,309 −0,3)2 +

+(0,422 −0, 4)2 +(0,487 −0,5)2 = 0,00025 м2 .

Замечание. Обычно вид адекватной модели заранее не известен. В этом случае дисперсия σe2 оценивается с использованием повторных опытов при фиксированных значениях факторов. Для этого, например, проводится специальная серия из L опытов при фиксированных значениях факторов, причем результаты этих опытов уже не используются для получения точечных оценок коэффициентов регрессии. Тогда точечную оценку дисперсии σe2 находим по формуле

чечной оценки bi минимальна в классе линейных несмещенных оценок, где ci+1 i+1 — элемент матрицы С, причем кова-

риация случайных величин bi и bj равна σ2e ci +1 j +1 .

11

Свойства 1 и 2 справедливы независимо от вида закона распределения случайной величины e. Если дополнительно предположить, что случайная величина e подчиняется нормальному закону N (0, σe ) , то можно сформулировать еще

одно свойство точечных оценок МНК.

3. Точечные оценки b0, b1, ..., bd подчиняются совместному (d +1) -мерному нормальному закону распределения и

совпадают с оценками, полученными методом максимального правдоподобия.

Пример 3. Определим дисперсию точечной оценки b, полученной МНК в примере 1.

Согласно второму свойству, имеем

Таким образом, дисперсия оценки b определена в долях от σe2.

Замечание. Если в примере 1 считать, что допустимо повторное проведение эксперимента и фактор t может изменяться в пределах от 0 до 50 с, то для достижения минимальной дисперсии D[b] следует выбрать t1 = ... = t5 = 50 с.

Тогда при одинаковом количестве опытов

что более чем в 2 раза меньше по сравнению с предыдущим вариантом.

12

3. СТАТИСТИЧЕСКИЙ АНАЛИЗ РЕЗУЛЬТАТОВ

Статистический анализ позволяет получить ответ на вопрос о пригодности регрессионной модели. Если модель непригодна, то ее необходимо изменить. Это приведет к построению более сложной математической модели и проверке ее пригодности и т. д. до тех пор, пока не будет получена пригодная математическая модель.

Статистический анализ, как правило, проводят в несколько этапов: проверка значимости коэффициентов регрессии; проверка адекватности регрессионной модели; проверка работоспособности регрессионной модели.

3.1. Проверка значимости коэффициентов регрессии

В результате этой проверки выясняется, обусловлено ли отличие bi от нуля чисто случайными обстоятельствами или же это отличие неслучайно и вызвано тем, что в теоретической регрессионной модели действительно присутствует соответствующий коэффициент регрессии, т. е. βi ≠ 0.

Проверка осуществляется путем вычисления статистик

где i = 0, …, d. Если |ti| не превосходит критического значения t , то соответствующий коэффициент регрессии полага-

ется незначимым и может быть исключен из регрессионной модели.

Критическое значение t равно значению tν, α/ 2 , которое

является квантилем уровня 1 −α/ 2 распределения Стьюдента и зависит от числа степеней свободы ν = νe и уровня значимости α (обычно α = 0,05 ). Значения квантилей tν,γ уровня 1 − γ распределения Стьюдента в зависимости от числа степеней свободы ν и вероятности γ приведены в табл. 2.

13

14

Конечным результатом после проверки значимости всех коэффициентов регрессии является регрессионная модель, содержащая лишь значимые коэффициенты β(j), где j = 0, …, d. Причем d +1 ≤ N , где d +1 — общее число значимых коэффициентов регрессии.

3.2. Проверка адекватности регрессионной модели

Такая проверка регрессионной модели имеет своей целью выяснение вопроса о том, правильно ли выбран вид модели. Проверка адекватности регрессионной модели возмож-

на при условии, что d +1 < N и известна точечная оценка Se2

дисперсии случайной величины e.

Если d +1 = N , то проверять адекватность регрессионной модели не имеет смысла, так как в этом случае поверхность, соответствующая уравнению регрессии, проходит точно через все экспериментальные точки.

При проверке адекватности используют статистику

F = Sост2 Se2 .

Если F не превосходит критического значения F*, то модель

адекватна. В противном случае говорят о наличии дополнительного рассеивания, обусловленного несоответствием модели реальному объекту. Тогда необходимо либо усложнить регрессионную модель, либо уменьшить интервалы варьирования факторов.

Критическое значение F* равно значению Fν1 , ν2 , α , кото-

рое является квантилем уровня 1 −α распределения Фишера и зависит от степеней свободы ν1 = N −d −1 , ν2 = νe и уров-

ня значимости α. Значения квантилей Fν1 , ν2 , α уровня 1 −α

распределения Фишера в зависимости от ν1, ν2 и вероятности α = 0,05 приведены в табл. 3.

15

После проверки адекватности регрессионной модели, содержащей лишь значимые коэффициенты регрессии, имеет смысл рассматривать вопрос о ее работоспособности.

3.3. Проверка работоспособности регрессионной модели

Необходимость такой проверки обусловлена тем, что нередко даже адекватная регрессионная модель на практике оказывается бесполезной, например, в силу своей низкой точности предсказания. Эта проверка может включать в себя несколько различных процедур, описанных ниже.

Исследование остатков. Остатки ei = yi − yi — это раз-

ности между фактически наблюдаемыми значениями yi в i-м опыте и значениями yi , предсказанными с помощью уравне-

ния регрессии

y (x1, x2 , ..., xn )= b(0) F(0) (x1, x2 , ..., xn )+

+b(1) F(1) (x1, x2 , ..., xn )+... +b(d ) F(d ) (x1, x2 , ..., xn ),

где b(0), b(1), ..., b(d) — точечные оценки значимых коэффициентов регрессии β(0), β(1), ..., β(d) соответственно.

Если регрессионная модель подобрана правильно, то остатки содержат информацию о свойствах случайной величины e. Тогда следует выяснить, не противоречат ли эти свойства предположениям, на которых основан весь анализ.

Вычисление точечной оценки коэффициента детерми-

нации. Коэффициент детерминации характеризует точностные свойства регрессионной модели, изменяясь в пределах от 0 до 1. Точечная оценка R2 коэффициента детерминации определяется по формуле

18

Здесь

где yi — значения отклика в i-м опыте; yi — значения, предсказанные с помощью уравнения регрессии; y — среднее значение отклика.

Если у модели R2 ≥ 0,75 ( Sост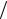Sy ≤ 0,5 ), то это обеспечивает уменьшение ошибки предсказания по крайней мере в 2 раза относительно примитивного предсказания по среднему значению отклика. Сопоставление точечной оценки коэффициента детерминации с R2 = 0,75 является простейшей процедурой, позволяющей получить общее представление о ценности найденной модели. Если число опытов велико по сравнению с числом коэффициентов в уравнении регрессии, то близость R2 к 1 говорит о хорошей точности регрессионной модели.

Дополнительные проверки. Они могут включать в себя выяснение правдоподобности регрессионной модели в соответствии с физикой протекающих в объекте процессов и рассмотрение ряда других вопросов, которые учитывают специфику задачи.

4. РЕШЕНИЕ ТИПОВОЙ ЗАДАЧИ

Механизм, состоящий из подвижной части, пружины и демпфера, соединен с неподвижным основанием. Под действием силы F(t) подвижная часть механизма перемещается по закону x(t), который является одинаковым для всех опытов. Расчетная схема механизма представлена на рис. 3.

19