6. Экстремум функции нескольких переменных

Определение. Функция z=f(x,y) имеет в точке М₀ максимум (минимум), если значение функции в этой точке наибольшее (наименьшее) по сравнению с точками, близкими к М₀.

Необходимые условия экстремума: если функция z=f(x,y) имеет в точке М₀ максимум (минимум), то ее частные производные первого порядка в этой точке равны нулю.

Отметим, что равенство нулю частных производных не означает существование экстремума (максимума или минимума). Например, для гиперболического параболоида (см. рис. 9) в точке (0,0) частные производные равны нулю, но эта точка не является ни максимумом, ни минимумом.

Достаточные условия экстремума функции двух переменных: если для функции z=f(x,y) в точке М₀ частные производные первого порядка равны нулю и значения вторых производных в этой точке равны

, , ,

то функция имеет максимум, если Δ=AּC-B²>0 при A<0, и минимум при A>0.

Задание 5. Исследовать на экстремум заданную функцию.

№	z=f(x,y)	№	z=f(x,y)
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Типовой пример. Исследовать на экстремум функцию .

Решение. Находим частные производные функции:

; .

Воспользовавшись необходимыми условиями экстремума, находим стационарные точки. Для этого решаем систему уравнений

откуда x=1; y=2. Таким образом, стационарной является точка M(1,2). Находим значения частных производных второго порядка в точке M:

; ; .

Составляем выражение .

Так как и , делаем вывод о наличии минимума в точке M(1,2). При этом минимальное значение функции . Для проверки и сравнения можно вычислить значение функции в точке, близкой к M(1,2).

7. Условные экстремумы функций нескольких переменных

Задачи на нахождение экстремумов функций нескольких переменных, в которых независимые переменные связаны между собой соотношениями, называются задачами на условный экстремум. Разъясним это понятие на простом примере функции двух переменных.

Пусть задана функция и линия AB с уравнением на плоскости (см. рис. 11). Задача состоит в том, чтобы на AB найти такую точку M₁, в которой значение функции является наибольшим по сравнению со значениями этой функции в точках AB, находящихся вблизи точки M₁. Такие точки называются точками условного экстремума функции z. В отличие от обычной точки экстремума значение функции в точке условного экстремума сравнивается со значениями функции не во всех точках некоторой ее окрестности, а только в тех, которые лежат на линии AB. Графиком функции является верхняя полусфера. Эта функция имеет максимум в точке , ему соответствует вершина полусферы (рис.10). Геометрически ясно, что для точек этой линии наибольшее значение функции достигается в точке 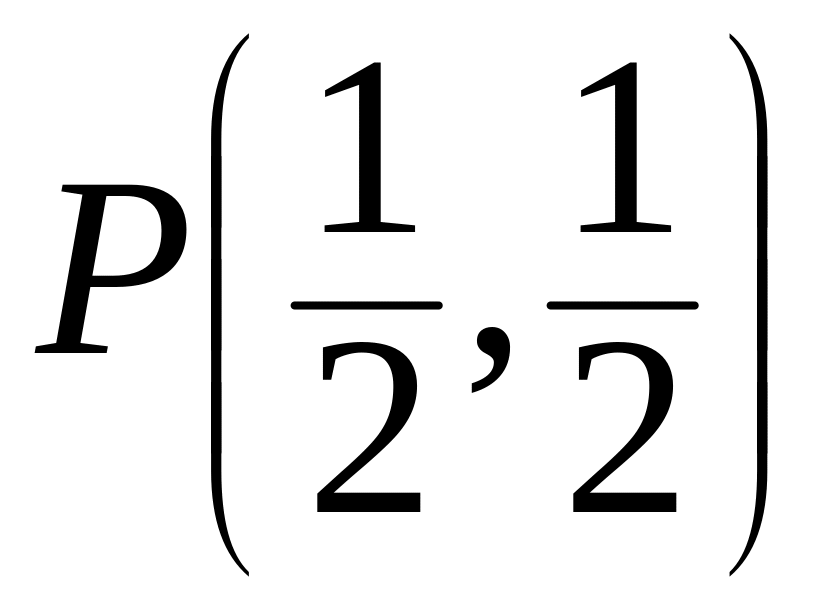, лежащей посередине между точками А и В. Это и есть точка условного экстремума (максимума) функции на данной линии, ей соответствует точка M₁ на полусфере.

z

M

M₁

O y

P B

A

x

Рис. 11

Правило. Для нахождения экстремума функции при условии необходимо составить вспомогательную функцию Лагранжа

,

(параметр играет вспомогательную роль) и для нее найти обычный экстремум, т.е. приравнять нулю частные производные

, , .

Типовой пример. Из данного куска жести площадью 2 нужно сделать закрытую коробку в форме параллелепипеда, имеющую наибольший объем.

Решение. Обозначим длину, ширину и высоту коробки через . Задача сводится к нахождению максимума функции при условии, что .