Контрольные вопросы

1. Как определяется градиент функции отклика?

2. От чего зависит величина составляющих градиента?

3. Как выбирается шаг движения по градиенту?

4. Что представляет мысленный опыт и алгоритмы его реализации?

5. Из какой точки плана начинают движение по градиенту?

6. В каком случае движение по градиенту считается эффективным?

7. Какие возможны исходы при крутом восхождении?

8. Как учитывается возможный временной дрейф при крутом восхождении?

Лекция 4 Ротатабельное планирование второго порядка

В некоторых случаях ортогональное планирование второго порядка не отвечает потребностям практики – при описании поверхности отклика, особенно в окрестностях точки оптимума, более значимой является оценка дисперсии уравнения в целом, чем оценка дисперсии отдельных коэффициентов полинома. В этом случае обычно стремятся к равномерности распределения информации в уравнении функции отклика по всем направлениям. Такому положению отвечают ротатабельные планы. Кроме сказанного, подобные планы второго порядка позволяют минимизировать систематические ошибки, связанные с неадекватностью представления результатов полиномами второго порядка.

Ротатабельным является такое планирование, у которого корреляционая матрица (Х^тХ)^-1 инвариантна к ортогональному вращению координат [2]. Это условие удовлетворяется для плана второго порядка, если все нечеткие моменты до четвертого порядка равны нулю, а для четных моментов имеет место соотношение:

(1)

где λ₂, λ₄ – некоторые константы, удовлетворяющие неравенству ;

N=2^k+2k+n₀ – общее количество опытов в плане; k – количество факторов.

Свойство ротатабельности не инвариантно к изменению масштабности независимых переменных. Вид информационного профиля зависит от λ₄ .

Иногда интерес представляет информация о функции отклика в некоторой окрестности центра плана. В этом случае следует добиться одинаковой погрешности модели внутри гиперсферы единичного радиуса. План, обеспечивающий такое свойство функции отклика, называется униформ-ротатабельным (λ₄<=1). При этом теряется ортогональность:

Для его формирования  достаточно обеспечить равенство дисперсии в центре плана (ρ = 0) и на поверхности гиперсферы радиуса ρ = 1. Этого добиваются подбором числа наблюдений n₀ в центре плана, а именно параметр λ₄ следует взять равным положительному корню квадратного уравнения [11]:

2λ₄ (λ₄ – 1)(k + 2) + λ₄ (k + 1) – (k – 1) = 0.

Ротатабельные планы с равномерным расположением точек на сфере приводят к выражденным матрицам (Х^тХ). Для устранения этого принимают комбинации ротатабельных планов с различным радиусом сферы.

 Точки ротатабельного центрального композиционного плана (РЦКП) Бокса второго порядка располагают на концентрических гиперсферах, количество которых не менее двух. Первая гиперсфера может быть вырожденной, т.е. представлять собой центральную точку плана, ее радиус ρ₁ = 0. Именно такая сфера часто используется на практике.

Вторая гиперсфера соответствует вписанному в нее кубу, выбранному в качестве ядра плана. Для ядра х_i =  1, следовательно, радиус этой гиперсферы равен:

ρ₂ = (х₁² + х₂² + … + х_k²)^1/2 = (k)^1/2.

Ядро представляет собой ПФЭ вида 2^k или ДФЭ вида 2^{k – p} , причем должно соблюдаться условие (k – p)/4 > 3/4. Следовательно, с учетом ограничений на ЦКП Бокса, если k ≥ 5, то в качестве ядра можно использовать полуреплику, если k ≥ 8, ядром может служить четверть реплики.

Третья гиперсфера имеет радиус ρ₃ = 2 ^{k / 4} для ядра в виде ПФЭ и радиус ρ₃=2^(k-p)/4 для ядра в виде ДФЭ.

Таким образом, каждый фактор в РЦКП Бокса варьируется на пяти уровнях. В некоторых случаях радиусы второй и третьей гиперсферы совпадают:

k = 2:

ρ₂ = 2 ^1/2, ρ₃ = 2 ^2/4 = 2^1/2;

k = 8 и p = 2:

ρ₂ = 8 ^1/2 = 2 ^3/2, ρ₃ = 2 ^{(8 – 2)/4} = 2^3/2.

Для каждого из факторов кроме нижнего, верхнего и основного уровней устанавливаются два дополнительных уровня “”, где  вычисляется по формуле:

,

где k – количество факторов.

В таблице 1 приведены необходимые сведения для составления ротатабельных центральных композиционных планов (РЦКП).

Таблица 1 - Сведения для составления ротатабельных центральных композиционных планов

Количество факторов	Число точек ПФЭ	Число звездных точек	Число точек в центре эксперимента	Значение α
2	4	4	5	1,414
3	8	6	6	1,682
4	16	8	7	2,000
5	32	10	10	2,378
5, полуреплика	16	10	6	2,000
6	64	12	15	2,828
6, полуреплика	32	12	9	2,378
7	128	14	21	3,333
7, полуреплика	64	14	14	2,828

Рассмотрим для примера случай объекта с двумя входными переменными (k = 2) [10]. Точки исходного симплексного плана находятся в вершинах равностороннего треугольника (рис.1).

Рисунок 1 – Построение РЦКП с двумя факторными переменными

Соединим точки в вершинах равностороннего треугольника с началом координат (находящемся в центре треугольника) и получим три вектора, концы которых дают еще три точки плана. Складывая вектора по три, получаем центральную точку. Первоначальные точки и новые точки дают ротатабельный план второго порядка.

В теории планирования эксперимента показано, что при помощи операции суммирования векторов, идущих из начала координат в вершины симплекса (с центром в начале координат), по два, по три и т. д. до k, можно при любом k построить множество точек, добавление которых к точкам исходного симплекса и добавляя к ним центральные точки получают ротатабельный план второго порядка. Полученные таким способом планы называют симплексно-суммируемыми.

Пример. В качестве примера рассмотрим матрицу рототабельного униформ-планирования второго порядка для k=3 [2]. При использовании полинома в качестве математической модели процесса факторы кодируют по формуле

где x_i – кодовое значение i-го фактора, z_i – натуральное текущее значение i-го фактора, z_i0 – начальный уровень фактора, ∆z_i – интервал варьирования i-го фактора.

Таблица 2 - Матрица планирования РЦКП (униформ-планирование)

второго порядка для k=3

x0	x1	x2	x3	x12	x22	x32	x1x2	x1x3	x2x3
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	-1 1 -1 1 -1 1 -1 1 -1,682 1,682 0 0 0 0 0 0 0 0 0 0	-1 -1 1 1 -1 -1 1 1 0 0 -1,682 1,682 0 0 0 0 0 0 0 0	-1 -1 -1 -1 1 1 1 1 0 0 0 0 -1,682 1,682 0 0 0 0 0 0	1 1 1 1 1 1 1 1 2,828 2,828 0 0 0 0 0 0 0 0 0 0	1 1 1 1 1 1 1 1 0 0 2,828 2,828 0 0 0 0 0 0 0 0	1 1 1 1 1 1 1 1 0 0 0 0 2,828 2,828 0 0 0 0 0 0	1 -1 -1 1 1 -1 -1 1 0 0 0 0 0 0 0 0 0 0 0 0	1 -1 1 -1 -1 1 -1 1 0 0 0 0 0 0 0 0 0 0 0 0	1 1 -1 -1 -1 -1 1 1 0 0 0 0 0 0 0 0 0 0 0 0

Коэффициенты модели и их дисперсии рассчитываются по формулам [11]:

,

;

;

;

;

;

;

.

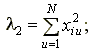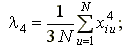
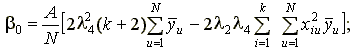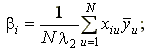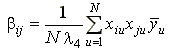Представленные формулы справедливы для ротатабельного планирования при любом количестве независимых переменных. Такое планирование не позволяет получить независимые оценки для всех коэффициентов модели, коррелированными оказываются коэффициенты (β₀, β_ii) и (β_ii, β_ij). Взаимную связь этих пар коэффициентов можно охарактеризовать ковариациями:

cov(β ₀, β _ii) = – 2σ²(ỹ) λ₄ A/N ;

cov(β _ii, β _ij) = σ² (ỹ) (1–λ₄ )A/N.

При использовании ротатабельных планов второго порядка отпадает необходимость в постановке дополнительных опытов для оценки дисперсии воспроизводимости. Дисперсию воспроизводимости определяют по опытам в центре плана. Вычисляется среднее значение

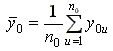
и величина дисперсии воспроизводимости

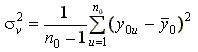
Дисперсия воспроизводимости будет несмещенной оценкой дисперсии ошибок наблюдения. При ненасыщенном планировании остаточная сумма

отличается от нуля. Здесь – величина, предсказанная уравнением модели, – найденная экспериментально.

Величина

σ_R² =S²_R / [N–(k+1)(k+2)/2]

характеризует неадекватность модели и также является несмещенной оценкой дисперсии ошибок наблюдения.

На основании рассчитанных величин можно провести все необходимые проверки коэффициентов и модели в целом. Адекватность модели проверяется по критерию Фишера:

.

Значимость коэффициентов модели проверяется по критерию Стьюдента аналогично определению значимости при ортогональном планировании эксперимента:

.

Если незначимым оказался один из квадратичных эффектов, то его следует исключить и коэффициенты уравнения регрессии пересчитать.