
- •Методы оптимальных решений
- •ОГЛАВЛЕНИЕ
- •3. ПОСЛЕДОВАТЕЛЬНОСТИ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ
- •3.1. Задачи о непрерывном начислении процентов
- •4.7. Метод наименьших квадратов
- •27. Предполагая, что между переменными х и у существует квадратическая зависимость у = а0 + а1х +а2х2, найти параметры этой зависимости, используя метод наименьших квадратов, по следующим опытным данным:
- •Методы оптимальных решений
а)
|
|
x |
|
1 |
|
2 |
|
5 |
|
6 |
|
|
|
|
|
y |
|
2,5 |
3,1 |
|
4,1 |
|
5,3 |
|
|||
б) |
|
|
|
|
|
|
|
|
|
|
|
||
|
x |
-1 |
|
1 |
|
2 |
3 |
|
5 |
|
6 |
|
|
|
y |
7,2 |
|
5,8 |
|
5 |
3,9 |
2 |
|
0 |
|
||
27. Предполагая, что между переменными х и у существует квадратическая зависимость у = а0 + а1х +а2х2, найти параметры этой зависимости, используя метод наименьших квадратов, по следующим опытным данным:
а)
x |
-1 |
1 |
3 |
4 |
6 |
y |
5,5 |
4,8 |
-2,3 |
-1,2 |
0,3 |
б)
x |
1 |
1,5 |
2 |
2,5 |
3 |
y |
2,2 |
3,1 |
2,4 |
2 |
1,3 |
28. Данные о среднесуточной переработке свёклы у ( тыс.ц) в зависимости от основных производственных фондов х ( тыс.руб.) приведены в таблице:
x |
175 |
225 |
275 |
325 |
376 |
y |
7 |
7,3 |
7,64 |
7,93 |
8,3 |
Предполагая, что между этими переменными существует линейная зависимость у=ах+b, найти параметры а и b , используя метод наименьших квадратов. Вычислить для х = 225 отклонение табличного значения у от соответствующего значения функции.
29. Рост продукции (млн руб.) некоторого завода по годам характеризуется следующими данными:
Год, х |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
Объём |
|
|
|
|
|
|
|
|
|
продукции, у |
8,2 |
6,0 |
8,7 |
10,0 |
16,5 |
20,3 |
30,0 |
38,5 |
54,7 |
|
|
|
|
42 |
|
|
|
|
|
|
Считая, что рост продукции |
задается |
квадратической |
зависимостью |
||||
у=а0+а1х+а2х2, найти параметры а0 |
, а1, а2 , |
используя метод |
наименьших |
|||||
квадратов. |
|
|
|
|
|
|
||
|
30. Данные о средней производительности труда |
за последние пять лет, |
||||||
представлены в следующей таблице: |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Год |
|
1 |
2 |
3 |
|
4 |
5 |
|
Средняя производительность |
|
|
|
|
|
|
|
|
труда |
|
235 |
250 |
270 |
|
292 |
300 |
Предполагая, что рост производительности труда следует линейному закону, определить параметры уравнения а и b, используя метод наименьших квадратов.
31. В таблице приведены значения выработки валовой продукции у (руб.) и производственной нагрузки на одного среднегодового работника х (усл.ед.)
|
Производственная |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
нагрузка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
на 1 |
работника |
|
20,2 |
|
|
22,4 |
24,5 |
25,8 |
31,5 |
|
34,4 |
|
|
36,7 |
|
38,1 |
|||||
|
(усл. ед.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Валовая |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
продукция |
на |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
одного |
средне- |
|
1 820 |
|
1 890 |
2 010 |
2 230 |
1 840 |
2 430 |
|
2 690 |
|
2 250 |
||||||||
|
годов. |
работника |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
(руб.) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
44,0 |
|
45,2 |
|
|
46,3 |
|
49,0 |
51,2 |
|
53,8 |
|
54,7 |
|
55,1 |
57,2 |
||||||
|
2 820 |
|
2 920 |
|
2 150 |
|
2 240 |
2 150 |
|
2 040 |
|
1 960 |
|
1 885 |
1 800 |
|||||||
|
Установить вид связи |
между рассматриваемыми |
показателями, |
найти |
||||||||||||||||||
уравнение этой связи, по |
методу |
наименьших квадратов. Найти значение |
||||||||||||||||||||
фактора х, при котором у достигает максимального значения. |
|
|
|
|
||||||||||||||||||
32.Себестоимость у (руб.) одного экземпляра книги в зависимости от тиража
х(тыс. экз.) приведены в таблице:
х |
1 |
2 |
3 |
5 |
10 |
20 |
30 |
50 |
100 |
200 |
у |
10,15 |
5,25 |
4,08 |
2,85 |
2,11 |
1,62 |
1,41 |
1,30 |
1,21 |
1,15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
43 |
|
|
|
|
|
Установить вид связи между рассматриваемыми показателями, найти уравнение связи, используя метод наименьших квадратов.
33. Выпуск продукции на предприятии характеризуется следующими данными:
Год |
2001 |
2002 |
2003 |
2004 |
2005 |
2006 |
2007 |
Выпуск |
|
|
|
|
|
|
|
продукции |
9,5 |
9,7 |
8,3 |
10,5 |
10,4 |
11,4 |
9,2 |
(млн руб.) |
|
|
|
|
|
|
|
Необходимо: а) установить вид зависимости выпуска продукции от времени и соответствующее уравнение по методу наименьших квадратов; б) пользуясь найденным уравнением, найти выпуск продукции в 2009 г.
34. В таблице приведены данные о выработке одним рабочим за смену изделий в зависимости от стажа его работы:
Cтаж, (лет) |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
Выработка |
|
|
|
|
|
|
|
|
одного рабочего |
|
|
|
|
|
|
|
|
за смену (шт.) |
80 |
100 |
90 |
120 |
110 |
130 |
150 |
160 |
Необходимо: установить вид зависимости выработки рабочего за смену от его стажа и найти параметры этой зависимости, используя метод наименьших квадратов.
35. Фактические данные о затратах на рекламу х и спросе на продукцию у приведены в таблице:
Затраты на |
13 |
14 |
|
15 |
18 |
20 |
22 |
рекламу |
|
|
|
|
|
|
|
Спрос |
11,6 |
12,9 |
|
14,1 |
17,2 |
18,7 |
20,9 |
Определить вид зависимости |
спроса на продукцию от затрат на рекламу, |
||||||
найти параметры этой зависимости, пользуясь методом наименьших квадратов.
44

5. ОПРЕДЕЛЁННЫЙ ИНТЕГРАЛ В ЭКОНОМИКЕ
5.1. Экономический смысл определённого интеграла. Пусть функция z = f(t) описывает изменение производительности некоторого производства с течением времени. Найдём объём продукции U, произведённой за промежуток времени [0; Т]. Если производительность не изменяется с
течением времени (f(t) – постоянная функция), то объём |
продукции |
U, |
||||||||||||
произведённой за некоторый промежуток времени [t, |
t+ |
t], задаётся формулой |
||||||||||||
U |
= |
f(t) |
t. В общем |
случае |
справедливо |
равенство |
U = f( ) t, где |
|||||||
|
[t, |
t+ t], которое оказывается тем более точным, чем меньше |
t. |
|
|
|||||||||
|
|
Разобьём |
отрезок |
[0,T] |
на промежутки |
|
времени |
точками: |
||||||
0 = t0 <t1 < t2 |
<….< tn = |
T. Для величины |
объёма |
|
продукции |
Ui, |
||||||||
произведённой |
за промежуток времени [ti-1, ti], |
имеем |
U |
= f( |
) |
t, где |
||||||||
|
|
|
|
|
|
n |
|
n |
|
|
|
|
|
|
i |
[ti-1, ti], |
ti = ti‒ ti-1, i = 1,2, ..., n. Тогда U |
Ui |
|
f ( i ) |
ti . |
|
|
|
|||||
|
|
|
|
|
|
i 1 |
|
i 1 |
|
|
|
|
|
|
При стремлении max ti |
к нулю каждое из использованных приближённых |
|||||||||||||
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
равенств становится всё более точным, поэтому U = |
lim |
|
|
f ( i ) |
ti .. |
|
|
|||||||
|
|
|
|
|
|
|
max ti |
0 |
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
i |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Используя |
определение |
определённого |
интеграла, |
окончательно |
||||||||||
получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
T |
|
|
|
|
|
|
|
|
|
|
T |
|
U = f (t)dt , т.е. если f(t) – производительность труда в момент t, то |
f (t)dt |
|||||||||||||
|
|
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
есть объём выпускаемой продукции за промежуток [0, T].
Величина и объём продукции, произведённой за промежуток [0, T], численно равны площади под графиком функции Z = f(t), описывающей изменение производительности труда с течением времени, на промежутке [0, T].
Пример 1. Известно, что численность населения определяется формулой y 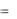 y0ekt , где y0 – число жителей в начальный момент времени. Известно также,
y0ekt , где y0 – число жителей в начальный момент времени. Известно также,
что потребление населением в единицу времени некоторого продукта пропорционально числу жителей. Пусть коэффициент пропорциональности равен q, тогда функция потребления Р(t) будет иметь вид: Р=q y=q∙ y0ekt . Найти объём продукта, необходимого для потребления на промежуток времени [t1, t2].
Решение. В малый промежуток времени dt (dt= t) количество жителей будем считать постоянным, следовательно, за этот элементарный промежуток времени
45

потребляется количество продукта dS = pdt = q· y0ekt dt. Интегрируя это равенство, получим количество S продукта, необходимое для населения на весь промежуток времени от t1 до t2 :
|
t |
2 qy |
|
ekt dt |
|
|
1 ekt |
|
t2 |
qy0 |
ekt2 ekt1 . |
|
|
|
|
|
|||||||
S= |
|
|
qy |
|
|
|
|||||
|
0 |
0 |
|
|
|
||||||
|
t1 |
|
|
k |
|
t |
k |
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
5.2. Восстановление функций экономического анализа по их предельным характеристикам. В зависимости от конкретного смысла функции f(x) (физического, геометрического, экономического) при интегрировании f(x) мы получаем выражение для соответствующего закона, описывающего данный объект. Так, по скорости (t) прямолинейного движения можно восстановить зависимость пути от времени t; по скорости распада радия можно найти закон распада радия и т.д. Характеристики экономических закономерностей также можно восстановить, если известна скорость (интенсивность, плотность) или темп роста (относительная скорость) соответствующего экономического процесса.
Зная предельные издержки производства y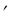 = f(x), можно найти издержки производства y = f(x) dx + c (здесь х – объём однородной продукции). Зная
= f(x), можно найти издержки производства y = f(x) dx + c (здесь х – объём однородной продукции). Зная
скорость y |
= f(x) (или темп |
y |
|
) изменения производительности труда, можно |
||||||
y |
||||||||||
|
|
|
|
|
|
|
|
|||
найти производительность труда |
y = |
f(t) dt + c. |
|
|
|
|
||||
|
|
|
|
|
x2 |
6x, если 0 |
x |
4, |
||
Пример |
2. Пусть f(x) |
= |
0, |
если |
4 x |
5, |
функция, |
|||
|
|
|
|
|
x2 13 x 40, |
если 5 |
x 8 |
|||
характеризующая изменение производительности труда; х – время, отсчитываемое от начала рабочего дня. Определить объём продукции, произведенной за весь рабочий день.
Решение. Объём произведённой продукции можно рассматривать как сумму объёмов продукции, произведённой за 4 часа работы до обеденного перерыва и за оставшиеся 3 часа работы:
46

4 |
( x2 |
6x)dx |
8 |
( x2 13x 40)dx |
x3 |
6 |
x2 |
|
4 |
x3 |
13x2 |
40x |
8 |
31,17( усл.ед.). |
|
|
|
|
|
|
|
|
|
|
|
||||||
0 |
|
|
5 |
|
3 |
2 |
|
0 |
3 |
2 |
|
5 |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||
Если в функции Кобба – Дугласа считать, что затраты труда есть линейная
зависимость от |
времени, а затраты |
капитала неизменны, то она примет |
вид: q(t) = ( t + |
) e t. Тогда объём выпускаемой продукции за Т лет составит |
|
|
T |
|
|
Q = |
( t + ) e t dt. |
|
0 |
|
Пример 3. Найти объём продукции, произведенной за 4 года, если функция Кобба – Дугласа имеет вид q(t) = 10 (1+t) e3t.
Решение. Применяя формулу интегрирования по частям, получим
4 |
|
|
|
u t 1 dv e3t dt |
|
10 |
|
|
|
10 |
4 |
10 |
|
|
|
10 |
|
4 |
|||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
||||||||||||||||
Q=10 (1 |
t) e3t dt |
|
|
|
|
|
|
1 |
|
3t |
|
|
e3t |
(t 1) |
|
e3t dt |
(5e12 |
1) |
|
e3t |
|
||||||
|
|
du dt v |
e |
3 |
0 |
|
3 |
3 |
|
9 |
0 |
||||||||||||||||
0 |
|
|
|
3 |
|
|
|
|
|
0 |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
10 |
(5e12 |
1) |
10 |
(e12 |
1) |
10 |
(14e12 |
2) |
2,53 106 |
( усл.ед.). |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
3 |
|
|
9 |
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пусть известна функция t = t(x), описывающая изменение затрат времени t на изготовление изделия в зависимости от степени освоения производства, где х – порядковый номер изделия в партии. Тогда среднее время tср, затраченное на изготовление одного изделия в период освоения от х1 до х2 изделий, вычисляется по теореме о среднем:
|
|
1 |
|
x2 |
|
tср |
|
|
t(x)dx . |
(5.1) |
|
|
|
|
|||
x2 |
|
|
|||
|
|
x1 x |
|
||
|
|
|
1 |
|
|
Функция изменения затрат времени на изготовление изделий t = t (x) обычно имеет вид t = ax-b, где a – затраты времени на первое изделие; b – показатель производственного процесса.
Пример 4. Найти среднее время, затраченное на освоение одного изделия в период освоения от х1 = 100 до х2 = 121 изделий, полагая а = 600 (мин), b = 0,5.
|
|
|
|
1 |
121 |
1 |
|
600 |
|
|
121 |
400 |
|
||
Решение. |
tср |
|
|
600x 2 dx |
2 x |
|
57,2 (мин). |
||||||||
|
|
|
|
|
|
|
|
||||||||
121 |
100 |
21 |
|
100 |
7 |
|
|||||||||
|
|
100 |
|
|
|
|
|
|
|
||||||
5.3. Определённый интеграл в финансовом анализе
Определение начальной суммы по её конечной величине, полученной через время t (лет) при годовом проценте (процентной ставке) р, называется
47

дисконтированием. Задачи такого рода встречаются |
при |
определении |
экономической эффективности капитальных вложений. |
|
|
Пусть Kt – конечная сумма, полученная за t лет, и |
К – |
дисконтируемая |
(начальная) сумма, которую в финансовом анализе называют также современной
суммой. Разность между конечной суммой |
Kt |
и дисконтируемой суммой К |
||||||||||
называется дисконтом: D = Kt – K. |
|
|
|
|
|
|
|
|
|
|
||
Если проценты простые, |
то Kt = K (1+i |
∙ |
|
t), где |
i |
|
p |
– удельная |
||||
|
|
|
|
|
||||||||
|
100 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|||
|
Kt |
|
|
|
|
|
|
|
|
|
|
|
процентная ставка. Тогда K |
|
. |
|
|
|
|
|
|
|
|
|
|
1 i t |
|
|
|
|
|
|
|
|
|
|
||
В случае сложных процентов Kt = K (1 + i ∙ t) |
t |
, поэтому |
|
K |
|
|
Kt |
. |
||||
|
|
|
i t)t |
|||||||||
|
|
|
|
|
|
|
(1 |
|
||||
Пусть поступающий ежегодно доход изменяется во времени и описывается функцией f(t) при удельной норме процента, равной i, процент начисляется непрерывно. Можно показать, что в этом случае дисконтированный доход К за время Т вычисляется по формуле
|
T |
|
K |
f (t)e it dt. |
(5.2) |
|
0 |
|
Пример 5. Определить дисконтированный доход за три года при процентной ставке 8%, если первоначальные капиталовложения составили 10 млрд руб. и намечается ежегодно увеличивать капиталовложения на 1 млрд руб.
Решение. |
По |
условию, капиталовложения задаются функцией |
|
f(t)=10+1 t=10+t. |
Тогда |
по |
формуле (5.2) дисконтированная сумма |
|
3 |
|
|
капиталовложений |
K |
(10 t) |
e 0,08t dt. |
|
0 |
|
|
Интегрируя, получим К = 30,5 млрд руб. Это означает, что для получения одинаковой наращенной суммы через три года ежегодные капиталовложения от 10 до 13 млрд руб. равносильны одновременным первоначальным вложениям 30,5 млрд. руб. при той же начисляемой непрерывно процентной ставке.
Рассмотрим задачу нахождения капитала (основных фондов) по известным чистым инвестициям. Чистые инвестиции (капиталовложения) – это общие инвестиции, производимые в экономике в течение определённого промежутка времени (чаще всего – года), за вычетом инвестиций на возмещение выходящих из строя основных фондов (капитала). Таким образом, за единицу времени капитал увеличивается на величину чистых инвестиций.
48

Если капитал обозначить как функцию времени K(t), а чистые инвестиции –
I(t), можно записать I (t) |
d |
K (t) . |
|
dt |
|||
|
|
Часто требуется найти приращение капитала за период с момента времени t1 до t2, т.е. величину K = K(t2) – K(t1). Замечая, что K(t) является первообразной для функции I(t) можно сразу записать:
|
|
t2 |
|
K K (t2 ) K (t1 ) |
I (t)dt. |
|
|
t1 |
|
З А Д А Ч И |
|
1.Непрерывная |
на отрезке [0,7] |
функция y = f(t) описывает |
производительность труда рабочего в любой момент времени t, отсчитываемый от начала рабочего дня в часах. Функция f(t) измеряется количеством продукции за час работы. Определить выработку рабочего за третий час работы.
2. Пусть f(t) – нагрузка в киловаттах на трансформаторную подстанцию в любой момент времени t, отсчитываемый в часах от начала суток. Найти расход электроэнергии потребителями за промежуток времени от 0 до 24 часов, если f(t) является непрерывной на этом промежутке.
3. Численность населения в любой момент времени t задаётся функцией y = f(t). Потребление некоторого продукта пропорционально численности населения с коэффициентом пропорциональности k. Считая f(t) непрерывной на рассматриваемом промежутке, найти объём потребления рассматриваемого продукта за первое полугодие второго года с момента начала отсчёта.
4. Пусть f(x)=‒ x2+9x – функция, характеризующая изменение производительности труда; х – отрезок времени, отсчитываемый от начала рабочего дня (0 х 8). Определить объём продукции, производимой во второй час рабочего дня.
5. Пусть f (x) |
4 |
x3 |
1 – количество товара, поступающего на склад |
|
27 |
||||
|
|
|
магазина, х – время, отсчитываемое от начала суток (0 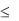 х
х 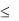 24). Подсчитать, какое количество товара поступает на склад с 12 до 15 часов.
24). Подсчитать, какое количество товара поступает на склад с 12 до 15 часов.
49

6. Определить объём продукции, произведённой рабочим за пятый час рабочего дня, если производительность труда характеризуется функцией
3
f (t) 5. 3t 2
7. |
Определить объём выпуска продукции при производительности |
|||
f(t) = 11,3t |
e-0,417t |
за первые пять часов работы. |
||
8. |
При непрерывном производстве химического волокна производительность |
|||
|
|
|
t |
|
аппарата |
|
|
1 (т/ч) растёт с момента запуска в течение 10 часов, а затем |
|
y(t) e5 |
||||
остаётся постоянной. Сколько волокна даёт аппарат в первые сутки после запуска?
9.Подсчитать выпуск продукции за 5 лет, если функция Кобба – Дугласа имеет вид q(t) = e t (t+1) (100-3t).
10.Пусть f(x) = 2x + 7 – количество стиральных машин, поступающих с завода в магазин за время х (в месяцах), отсчитываемое от начала поступления стиральных машин в магазин. Подсчитать среднее количество машин, поступивших в магазин за 4 месяца.
11.Найти среднее значение издержек К(х) = 3х2 + 4х + 2, выраженных в денежных единицах, если объём продукции х меняется от 0 до 3 единиц. Указать объём продукции, при котором издержки принимают среднее значение.
|
|
12. |
Среднее время освоения данного производства |
задается |
формулой |
||||
|
|
|
|
1 |
|
x2 |
|
|
|
t |
|
|
|
|
ax bdx. |
Найти среднее время освоения производства изделий, если |
|||
ср |
|
|
|
|
|||||
|
|
|
|
||||||
|
|
x2 |
|
x1 x |
|
|
|
||
|
|
|
|
|
|
|
|||
|
|
|
|
|
1 |
|
|
|
|
затраты времени на освоение первого изделия этой серии |
а = 2 |
нормочаса; |
|||||||
b = 0,2 и номера изделий осваиваемой партии изменяются от х1 = 5 до х2 = 10.
13. В 2002 году в некотором городе проживало 380 000 жителей, а в 2007 году – 402 000. Найти среднюю численность населения в этом городе,
50
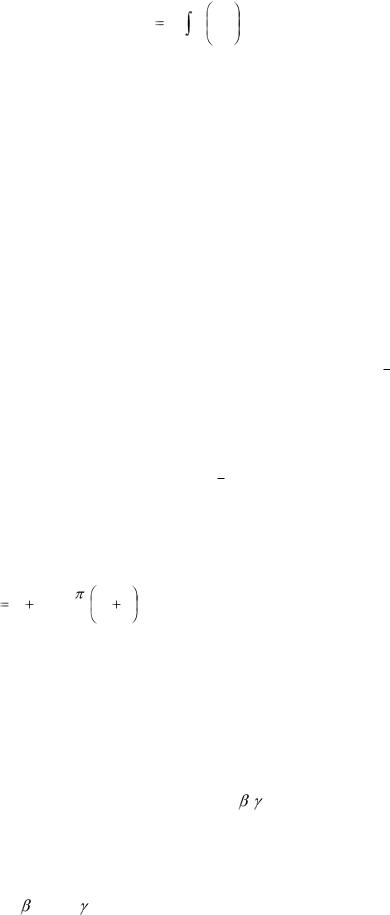
|
|
|
|
|
|
|
|
t |
|||
|
|
1 |
T |
|
ST |
|
|
|
|
|
|
|
|
|
|
T |
|
|
|||||
используя формулу S |
|
|
S0 |
|
|
|
|
dt , где S – средняя численность населения; |
|||
|
T |
|
S0 |
||||||||
|
|
|
0 |
|
|
|
|
|
|
||
T – период наблюдений; |
|
S0 – численность населения к началу периода; |
|||||||||
ST – численность населения к концу периода.
14.Вычислить дисконтированный доход за 5 лет при условии, что годовой доход – f(t) = 400 000 руб., а удельный процент i = 4%.
15.Найти дисконтированный доход за бесконечный промежуток времени при условии, что f(t) = 50 000, i =5%.
16. Вычислить начальный вклад К, если выплаты должны составлять 100 усл. ед. в течение 4 лет, а процентная ставка равна 7.
17. По заданным чистым инвестициях I(t)=7000 
 t . Определить приращение капитала за три года.
t . Определить приращение капитала за три года.
18. Через сколько лет приращение капитала составит 80 000, если чистые инвестиции равны I(t) = 6 000 
 t .
t .
|
19. Зависимость нагрузки на трансформаторную подстанцию (в киловаттах) |
|||||||
от |
времени |
суток t |
(в часах от |
начала суток) |
выражается формулой |
|||
y |
a b cos |
|
|
t |
3 . |
Определить |
суммарный |
расход электроэнергии |
|
|
|
||||||
12 |
2 |
|||||||
потребителями за время от 0 до 24 часов. Провести расчёт при следующих числовых данных: а = 25 тыс.кВт, b = 15 тыс. кВт.
20. Определить объём финансирования на данный момент времени t работ по бурению нефтескважины, если затраты y на бурение каждого метра возрастают с глубиной скважины х по закону y=y0+аx, а скорость проходки скважины убывает со временем по закону - t, где а,  и
и 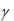 некоторые положительные константы и t – время в днях. Рассчитать необходимые средства финансирования в период с t1 до t2, время, необходимое для проходки скважины глубиной в 1 000 метров, и необходимый для этого объём финансирования работ при y0=150 000,
некоторые положительные константы и t – время в днях. Рассчитать необходимые средства финансирования в период с t1 до t2, время, необходимое для проходки скважины глубиной в 1 000 метров, и необходимый для этого объём финансирования работ при y0=150 000,
а=5, =10 и =0,02.
51
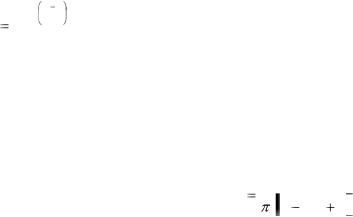
21. При строительстве дома затраты труда на возведение каждого следующего метра по сравнению с предыдущим возрастают на 2%. Определить суммарные затраты труда на возведение дома высотой в 60 м, если затраты на возведение первого метра дома составляют 1 000 ед. труда. Найти, за какой период может быть закончено строительство, если в течение дня может быть использовано 1 000 ед. труда.
|
|
|
x a |
2 |
|
|
|
|
|
22. Пусть |
y N |
e 50 |
характеризует число лицевых счетов, сумма вкладов |
|
|
0 |
|
|
|
которых заключена между х и х+1. Определить общую сумму вкладов в сберкассе и среднюю величину вклада, если а=100 и общее число вкладчиков составляет N0 =1 000 человек.
23. Распределение данного числа N0 человек по величине месячного дохода
(х) характеризуется следующей формулой: y |
|
N0 |
|
, где N0=1 000 и |
|
(x |
a)2 |
1 |
|||
|
|
а =100 руб. Определить среднюю величину месячного дохода.
6. ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ
Дифференциальные уравнения имеют многочисленные приложения в экономике, в изучении закономерностей общественных процессов. Основная сложность их применения состоит в составлении уравнений. Исчерпывающих правил для составления дифференциальных уравнений нет. Рассмотрим некоторые рекомендации.
Составление дифференциального уравнения по условию конкретной задачи включает обычно следующие основные этапы:
а) рассматриваем изучаемый процесс на достаточно малом промежутке его изменения (отрезок времени ∆t, приращение ∆х фактора, определяющего течение процесса) и предполагаем, что на этом промежутке течение процесса подчиняется достаточно простым закономерностям (линейной зависимости, пропорциональности, постоянстве некоторых факторов);
52

б) на выбранном промежутке составляем математическое описание процесса, связывая приращение искомой функции, характеризующей процесс, с другими переменными и постоянными в соответствии с условиями задачи;
в) переходим к пределу, заменяя приращения дифференциалами соответствующих переменных. В результате получаем описание процесса в форме дифференциального уравнения.
6.1. Дифференциальные уравнения в социологических исследованиях.
Предположим, что некоторое сообщение распространяется среди множества N человек. Предполагая, что число встреч для передачи информации за время ∆t пропорционально количеству людей, уже владеющих этой информацией, количеству людей, не владеющих информацией, и промежутку времени ∆t, определить закон распространения сообщения во времени.
Обозначим число людей, владеющих информацией через ∆у. Тогда, согласно условию задачи, число встреч для передачи информации (число людей
получающие информацию |
y за время |
t) будет определяться равенством ∆у = |
|||||||||||||||||||||
ky (N – y) ∆t. Переходя к пределу при ∆t →0, получим |
|
dy = ky (N – y) dt. |
|||||||||||||||||||||
Разделяем переменные и интегрируем: |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
dy |
|
|
kdt |
|
|
dy |
|
|
kdt; |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
y(N y) |
|
|
|
y(N y) |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
1 |
ln y |
ln |
N |
y |
1 |
ln c kt |
ln |
|
y.c |
|
Nkt; |
|||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
N |
|
|
|
|
|
|
|
|
|
|
N |
|
|
|
|
|
|
N |
y |
|
|
|
|
|
|
|
|
|
|
|
yc |
|
|
eNkt |
|
y |
|
N |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
N |
y |
|
1 ce |
Nkt |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Постоянную с можно определять из начальных условий: у(0) = у0. Частное |
|||||||||||||||||||||||
решение: y |
|
|
|
N |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
N |
y0 |
e |
Nkt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
y0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
График этой кривой экономисты называют логистической. Коэффициент k характеризует скорость передачи информации.
Широкое распространение в социологии имеет также модель процесса непрерывного роста (убывания). Пусть из статистических материалов известно, что число новорождённых за год пропорционально численности населения с коэффициентом пропорциональности k1, а число умерших за год также пропорционально численности населения с коэффициентом пропорциональности k2. Найти формулу, определяющую численность населения
53
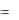
в любой момент времени t, если известна численность населения у0 в момент t=0. Предполагается, что не имеет места эмиграция и иммиграция.
Обозначим численность населения в момент времени t через у, тогда по условию задачи число родившихся за единицу времени равно k1у, а число умерших – k2у. Прирост населения за единицу времени выражается разностью k1y – k2y = (k1 – k2) ydt, а за малый промежуток времени dt: dy = (k1 – k2) ydt.
Число k1 – k2 = k называют коэффициентом естественного прироста. Проинтегрировав уравнение, получим:
у = С е k t.
Используя начальное условие у(0) = у0, находим С = у0. Поэтому искомая формула принимает вид: у = у0 е k t. При k > 0 получаем рост численности населения, при k< 0 – убывание, при k = 0 численность населения сохраняется стабильной во времени.
В ряде задач две переменные величины х и время t, участвующие в них, обладают тем общим свойством, что скорость изменения одной из них (х) по отношению к другой (t) пропорциональна наличному количеству величины х в
рассматриваемый момент времени t. |
|
|
|
|
|
|
|
|||
Учитывая, что скорость |
изменения величины х |
есть |
производная |
dx |
, |
|||||
dt |
||||||||||
|
|
|
|
|
|
|
|
|
||
обозначив |
коэффициент |
пропорциональности |
через |
k, |
получим |
|||||
дифференциальное уравнение, описывающее этот процесс: |
dx |
|
kx. |
|
|
|
||||
dt |
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||
Разделяя переменные и интегрируя, получим x = C∙ekt. |
|
|
|
|
|
|
|
|||
Решением является показательная функция. Условие задачи должно содержать данные:
1)для определения произвольной постоянной, т.е. значение х0 величины х в момент времени t = t0: x (t0) = x0;
2)для определения коэффициента пропорциональности k.
Уравнение описывает процесс непрерывного роста (при k >0) или непрерывного убывания (при k <0).
6.2. Модель естественного роста выпуска. Будем полагать, что некоторая продукция продаётся по фиксированной цене Р. Обозначим через Q (t) количество продукции, реализованной на момент времени t; тогда на этот момент времени получен доход, равный P∙Q(t). Пусть часть указанного дохода расходуется на инвестиции в производство реализуемой продукции, т.е.
54

I (t) = m PQ (t), |
(6.1) |
где m – норма инвестиции, постоянное число, причём 0< m < 1.
Если исходить из предположения о ненасыщаемости рынка (или о полной реализации производимой продукции), то в результате расширения производства будет получен прирост дохода, часть которого опять будет использована для расширения выпуска продукции. Это приведёт к росту скорости выпуска (акселерации), причём скорость выпуска пропорциональна увеличению инвестиций, т.е.
Q |
= I, |
(6.2) |
где 1/ – норма акселерации. Подставив в (6.2) формулу (6.1), получим |
||
Q = kQ, где k = mP. |
(6.3) |
|
Дифференциальное уравнение |
(6.3) представляет |
собой уравнение |
первого порядка с разделяющимися переменными. Общее решение этого
уравнения имеет вид |
|
|
|
|
|
Q = C ekt, |
|
|
|
где С – произвольная постоянная. |
|
|
|
|
Пусть в начальный момент времени t = t0 |
зафиксирован (задан) |
объём |
||
выпуска продукции Q0 , тогда |
Q0 = C ekt0 . Из этого |
условия |
можно |
|
выразить постоянную C = Q0 |
e kt0 . Отсюда |
получаем |
частное решение |
|
уравнения (6.3) – решение задачи Коши для этого уравнения:
Q = Q0 ek t t0 . |
(6.4) |
Данную модель называют моделью естественного роста выпуска.
Усложним условия модели и рассмотрим рост выпуска в условиях конкуренции. Будем полагать, что рынок не насыщается. Пусть P = P (Q) – убывающая функция, т.е. с увеличением объёма продукции на рынке цена на неё падает: dP/dQ < 0. Теперь из формул (6.1) – (6.3) мы получаем нелинейное дифференциальное уравнение первого порядка относительно Q с
разделяющимися переменными: |
|
Q = P (Q)Q, |
(6.5) |
где α = m.
Поскольку все сомножители в правой части этого уравнения положительны,
то Q > 0 , т.е. функция Q (t) возрастающая. |
Характер возрастания функции |
||||
определяется её второй производной. Из уравнения (6.5) получаем |
|||||
Q = Q P(Q) Q |
dP |
Q |
Q P |
dP |
Q . |
|
|
||||
|
dQ |
|
dQ |
||
55 |
|
|
|
|
|
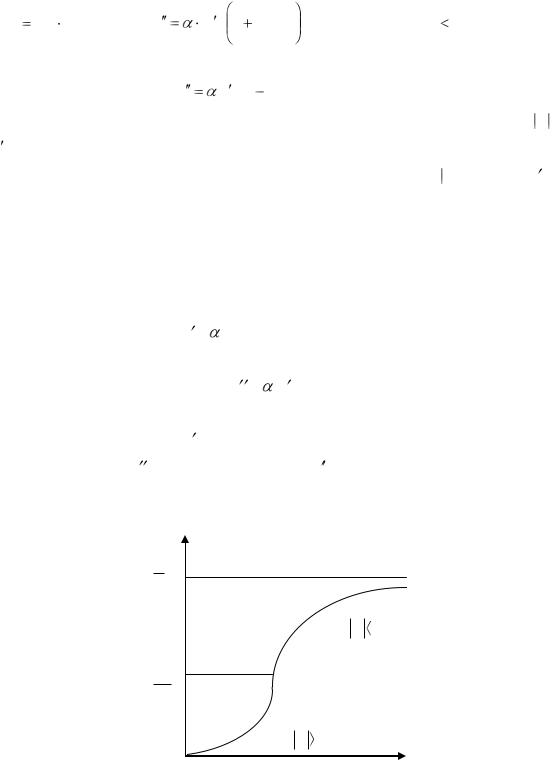
Это равенство можно преобразовать, введя эластичность спроса
E (P) |
dQ |
|
P |
, откуда Q |
Q P 1 |
dP |
|
Q |
, или, так как |
dQ |
0 , значит, Е(Р)<0, |
|
|
|
|
|
|
|
|
|
|||||
|
dP Q |
|
dQ P |
dP |
|
|||||||
окончательно получаем |
|
|
|
|
|
|
|
|
||||
|
|
|
|
Q |
Q P(1 1/ | E |). |
|
|
(6.6) |
||||
Из уравнения (6.6) следует, что при эластичном спросе, |
т.е., когда Е > 1, |
|||||||||||
Q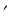 > 0 и график функции Q(t) имеет направление выпуклости вниз, что означает прогрессирующий рост; при неэластичном спросе, когда Е
> 0 и график функции Q(t) имеет направление выпуклости вниз, что означает прогрессирующий рост; при неэластичном спросе, когда Е < 1, Q
< 1, Q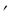 < 0 – направление выпуклости функции Q(t) вверх, что означает замедленный рост
< 0 – направление выпуклости функции Q(t) вверх, что означает замедленный рост
(насыщение). |
|
|
Для простоты примем зависимость в виде линейной функции |
|
|
|
P(Q) = a-bQ, a>0, b>0. |
(6.7) |
Тогда уравнение (6.5) имеет вид |
|
|
|
Q = (a – bQ)Q, |
(6.8) |
откуда |
Q = Q (a - 2bQ). |
(6.9) |
Из соотношений (6.8) и (6.9) получаем: |
|
|
|
Q = 0 при Q = 0 и при Q = a/b, |
|
Q |
> 0 при Q < a/(2b) и Q < 0 при Q > a/(2b); |
|
Q = a/(2b) – точка перегиба графика функции Q = Q (t). |
|
|
Q
a
b
E 1
a
2b
E 1
0 |
t |
Рисунок 6.1– график логистической кривой
Приведённый на рисунке 6.1 график функции (одной из интегральных кривых дифференциального уравнения) носит название логистической кривой.
56

Аналогичные кривые характеризуют и другие процессы, например размножение бактерий в органической среде обитания, динамику эпидемий внутри ограниченной общности биологических организмов и др.
Пример 1. Пусть изучается некоторый показатель экономического процесса y = f(t) в зависимости от времени. Функция f(t) дифференцируема, требуется
вывести темп изменения функции в данный момент времени Т = yy .
.
Решение. Данное соотношение является дифференциальным уравнением. При заданном законе изменения темпа во времени, т.е. при T = y(t), оно
позволяет определить закон изменения у: |
y |
(t), |
|
dy |
(t)dt . |
||
|
|
|
|||||
y |
|
y |
|||||
|
|
|
|
|
|
||
Интегрируя и учитывая |
начальные условия у = у0 |
при t = 0, получим частное |
|||||
решение y= e |
(t )dt . Если |
темп постоянен |
(Т0), |
то формула примет вид |
|||
y = eT0t . |
|
|
|
|
|
|
|
Пример 2. Ежедневный уровень выпуска продукции у возрастает со средним темпом роста Т0 = 0,1%. Определить закон изменения уровня выпуска продукции во времени и суммарный выпуск продукции за 1 месяц (25 рабочих дней), если уровень выпуска в начале месяца составляет 200 единиц в день.
Решение. Определим уровень выпуска из соотношения: y = 200 e0,001 t. Тогда объём выпуска продукции за месяц получим, вычислив интеграл:
25 |
25 |
200 |
|
|
25 |
|
V= ydt |
200 e0,001t dt |
|
e0,001t |
200 000 e0,025 1 . |
||
0,001 |
||||||
0 |
0 |
|
0 |
|||
|
|
|
||||
Пример 3. Пусть эластичность производственной функции y = f(x) относительно переменной х характеризуется соотношением:
x 2x2
Ех(y) = 1 x x2 .
Определить саму функцию, если её график проходит через точку М(1, 2).
Решение. Так как Ех(y)= |
x |
|
dy |
, то |
x |
|
dy |
|
x |
2x2 |
. |
y |
|
dx |
y |
|
dx |
1 |
x x2 |
||||
|
|
|
|
|
|||||||
Решая данное дифференциальное уравнение, получим: y = с (1 + х – х2). Найдём частное решение:
2 = с (1 + 1 – 1), с = 2;
57

иу = 2 (1 + х – х2).
6.3.Модель рынка с прогнозируемыми ценами. В простых моделях рынка обычно полагают, что спрос и предложение зависят только от текущей цены на товар. Однако в реальных ситуациях они зависят ещё и от тенденции ценообразования, и от темпов изменения цены. В моделях с непрерывными и дифференцируемыми по времени t функциями эти характеристики описываются соответственно первой и второй производными функции цены P(t).
Пусть функции спроса D и предложения S имеют следующие зависимости от цены P и её производных:
D(t) |
= 3 P |
- P - 2P + 18; |
|
S(t) |
= 4 P |
+ P - 3P + 3. |
(6.10) |
Принятые в (6.10) зависимости вполне реалистичны: поясним слагаемые с производными функции цены.
1. Спрос подогревается темпом изменения цены: если темп растёт (P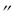 > 0), рынок увеличивает интерес к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус .
> 0), рынок увеличивает интерес к товару, и наоборот. Быстрый рост цены отпугивает покупателя, поэтому слагаемое с первой производной функции цены входит со знаком минус .
2. Предложение в ещё большей мере усиливается темпом изменения цены, поэтому коэффициент при Р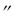 в функции S(t) больше, чем в D(t). Рост цены также увеличивает предложение, поэтому слагаемое, содержащее P , входит в выражение для S(t) со знаком “плюс”.
в функции S(t) больше, чем в D(t). Рост цены также увеличивает предложение, поэтому слагаемое, содержащее P , входит в выражение для S(t) со знаком “плюс”.
Требуется установить зависимость цены от времени. Поскольку равновесное состояние рынка характеризуется равенством D = S, приравняем правые части
уравнений (6.10). После приведения подобных получаем |
|
Р + 2 Р + 5 Р = 15. |
(6.11) |
Соотношение (6.11) представляет линейное неоднородное дифференциальное уравнение второго порядка относительно функции P(t). Общее решение такого уравнения состоит из суммы какого-либо его частного решения и общего
решения соответствующего однородного уравнения: |
|
|
Р |
+ 2 Р + 5P = 0. |
(6.12) |
Характеристическое уравнение имеет вид |
|
|
|
k2 + 2k + 5 = 0. |
|
Его корни – комплексно сопряжённые числа, |
и, следовательно, общее |
|
решение уравнения (6.12) |
даётся формулой |
|
|
58 |
|

~ |
t |
(С1 cos2t C2 sin 2t) |
P (t) e |
|
|
|
|
, |
где С1 и С2 – произвольные |
постоянные. В качестве частного решения |
|
неоднородного уравнения (6.11) возьмём решение P = Pst – постоянную величину как установившуюся цену. Подстановка в уравнение (6.11) даёт значение Pst = 3.
Таким образом, общее решение уравнения (6.11) имеет вид
P(t) = 3 + e-t (C1 cos 2t |
+С2 sin 2t). |
||
Нетрудно видеть, что P(t) |
Рst = 3 при |
t |
, т.е. все интегральные |
кривые имеют горизонтальную асимптоту P = 3 |
и колеблются около неё. Это |
||
означает, что все цены стремятся к установлению с колебаниями около установившейся цены Pst, причём амплитуда этих колебаний затухает со временем.
ЗА Д А Ч И
1.Скорость обесценивания оборудования вследствие его износа пропорциональна его фактической стоимости. Начальная стоимость А0. Какова будет стоимость оборудования по истечении t лет?
2.Производительность труда рабочего в течение смены является функцией времени t. Скорость изменения производительности труда подчиняется закону
y′ = 2at + b, где а и b – заданные постоянные. Найти закон изменения производительности труда во времени, если в момент времени t = 0 она равна у0.
3. Пусть некоторое сообщение распространяется среди 200 студентов, проживающих в общежитии. Предположим, что за 10 минут один студент сообщает информацию пяти студентам. Определить время, за которое: а) половина студентов; б) все студенты будут проинформированы.
4. Пусть |
эластичность |
производственной |
функции |
y = f(x) |
||||
характеризуется формулой Ех(y)= |
|
2x |
. Определить саму функцию, если её |
|||||
|
|
|
||||||
x2 |
4x 3 |
|||||||
|
|
|
|
|
||||
график проходит через точку (4; 3).
59
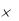
5. Численность населения города на 1 января 2008 г. составляла 600 тыс. человек. Найти численность населения: 1) на 1 января 2010 года, считая, что коэффициент k = 0,002 и не имеет места эмиграция и иммиграция; 2) на 1 января 2010 г., если коэффициент k = -0,001 и в течение каждого года эмигрирует 2% населения.
6. Пусть первоначальная численность некоторой популяции N0. Предположим, что в популяции численности N за малый промежуток времени dt происходит α∙N∙dt рождений и β∙ N∙dt смертей, где α и β – постоянные коэффициенты, характеризующие рождаемость и смертность данной популяции. Составить дифференциальное уравнение процесса. Найдите форму популяционной кривой. Определите, когда популяция вымирает, когда она сохраняет постоянную численность и когда она возрастает.
7. ЛИНЕЙНАЯ АЛГЕБРА
Линейная алгебра – один из разделов математической науки – имеет очень важное значение для экономистов, значительная часть математических моделей экономических процессов записывается в матричной форме.
Используя матричную запись условия экономической задачи, можно найти её решение с помощью правил всевозможных действий над матрицами (сложение, вычитание, умножение матрицы на число, обращение матрицы, умножение матриц и т.д.).
Приведём пример таких задач, предварительно ознакомившись с некоторыми теоретическими сведениями о матрицах.
7.1. Основные сведения о матрицах. Матрицей размера m n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Обозначаются матрицы буквами латинского алфавита : A; B; C; K; E. Например
60
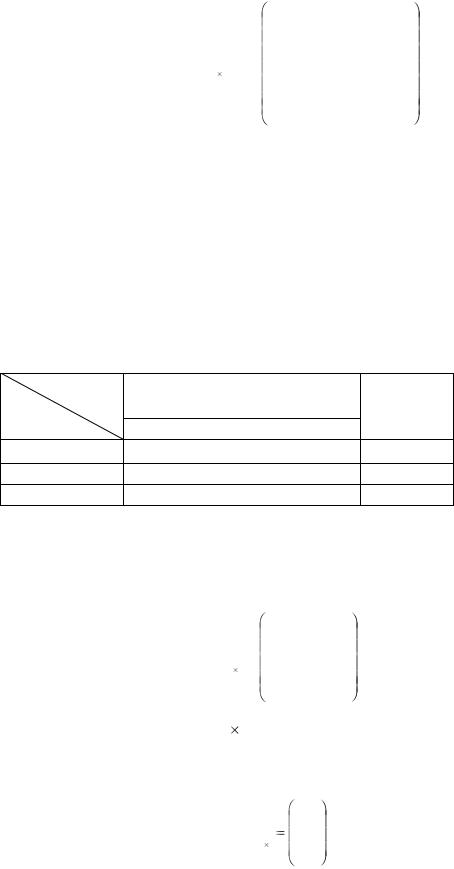
A =
m n
a11 ... a1k ...
a21 ... a2k ...
... |
... |
ai1 ... aik ... |
|
... |
... |
am1 ... |
amk ... |
a1n a2n
...
ain
...
amn
Числа, составляющие матрицу, называют элементами матрицы и обозначаются строчными буквами с двумя индексами – аik, i – номер строки, к – номер столбца.
С помощью матриц удобно записывать некоторые экономические зависимости.
Пример 1. Пусть имеется предприятие, выпускающее 4 вида изделий из трех |
|||||
видов сырья. |
|
|
|
|
|
|
Вид |
Затраты сырья на 1 ед. |
Запасы |
||
Вид |
прод. |
продукции (усл. ед) |
ресурсов |
||
сырья |
1 |
2 |
3 |
4 |
|
|
|
||||
I |
3 |
5 |
1 |
4 |
200 |
II |
2 |
10 |
7 |
8 |
300 |
III |
6 |
1 |
5 |
9 |
220 |
Тогда таблица расхода каждого вида сырья на выпуск 1 единицы продукции может быть записана в виде матрицы А
|
|
3 |
5 |
1 |
4 |
A = |
2 |
10 |
7 |
8 |
|
3 |
4 |
6 |
1 |
5 |
9 |
.
Размерность этой матрицы 3 4. В этой записи элемент а23=7 показывает, сколько ресурса второго вида необходимо затратить для производства одной ед. третьего вида продукции. Запас ресурсов можно записать в виде матрицы R:
200
R 300
3 1
220 .
Матрица состоит из 3 строк и одного столбца. Элемент r21 показывает запас ресурса второго вида.
61
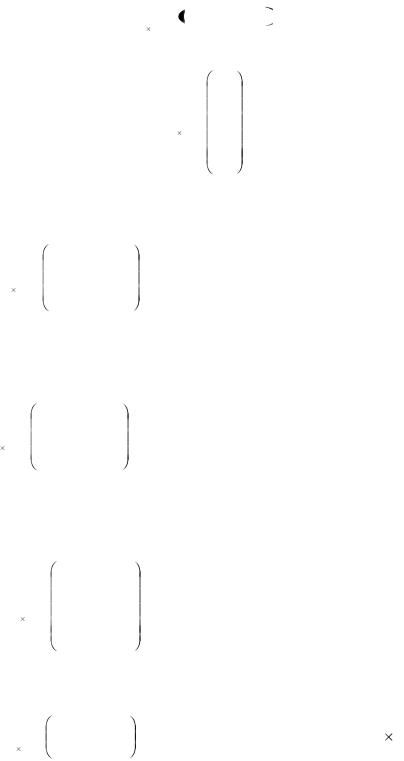
7.2. Виды матриц. Матрица, состоящая из одной строки, называется
матрицей строкой:
A = a11 a12 a1n .
1 n
Матрица, состоящая из одного столбца, называется матрицей столбцом:
k11
k 21
K = k31 m 1
.....
k m1 .
Матрица называется квадратной m-го порядка, если число строк этой матрицы равно числу ее столбцов и равно m. Например,
|
b11 |
b12 |
b13 |
|
B = b21 |
b22 |
b23 |
– квадратная матрица 3-го порядка, |
|
3 |
3 |
|
|
|
|
b31 |
b32 |
b33 |
|
элементы b11, b22, b33, – называются диагональными.
Если все недиагональные элементы квадратной матрицы равны нулю, то матрица называется диагональной.
|
с11 |
0 |
0 |
|
С = 0 |
с22 |
0 |
– диагональная матрица 3-го порядка. |
|
3 |
3 |
|
|
|
|
0 |
0 |
с23 |
|
Если у диагональной матрицы m-го порядка все диагональные элементы равны единице, то матрица называется единичной матрицей m-го порядка. Обозначается единичная матрица буквой Е.
1 0 0 0
E = |
0 |
1 |
0 |
0 |
– единичная матрица 4-го порядка. |
|
4 |
4 |
0 |
0 |
1 |
0 |
|
|
|
0 |
0 |
0 |
1 |
|
Матрица любого размера называется нулевой, если все её элементы равны нулю.
O |
= |
0 |
0 |
0 |
0 |
– нуль-матрица, размерностью 2 4. |
||
0 |
0 |
0 |
0 |
|||||
2 |
4 |
|
|
|||||
|
|
|
|
|
|
|||
Две матрицы К и В одной размерности, называют равными, если равны их соответствующие элементы, т.е. kij = bij, для любых i=1,2,..,m; j=1,2,..;n.
62

7.3. Операции |
над матрицами. Над |
матрицами можно производить |
|||
ряд операций. |
|
|
|
|
|
1. Умножение матрицы на число |
|
|
|
||
Произведением |
матрицы А на число |
называется матрица С= А, элементы |
|||
которой cij= aik, для i=1,2,..,m, ; k=1,2,..,n. |
|
|
|||
|
|
|
a11 |
a12 ... |
a1n |
|
C= A= |
|
a21 |
a22 ... |
a2n |
|
... |
|
... |
... |
|
|
|
|
|||
|
|
|
am1 |
am 2 ... |
amn . |
Следствие: общий множитель всех элементов можно вывести за знак матриц. Произведение матрицы А на число нуль есть нулевая матрица, т.е. 0 А=0 (нуль матрица).
2. Сложение матриц
Суммой двух матриц К и В одинакового размера (m n), называется матрица С=К+В, элементы которой cij=кij+bij, где i=1, m ; j=1, n .
Пример 2. Данные о совокупных продажах (в тыс. руб.) некоторого торга в 1-м и 2-м кварталах определённого года, записаны соответственно матрицами
|
48 |
51 |
38 |
70 |
|
35 |
40 |
30 |
60 |
K = 30 |
45 |
48 |
60 ; |
B = 20 |
40 |
40 |
50 |
||
3 |
4 |
|
|
|
3 |
4 |
|
|
|
|
50 |
48 |
51 |
58 |
|
45 |
45 |
50 |
52 . |
Требуется записать в виде матрицы данные о совокупных продажах (в тыс. руб.) на 1-е полугодие рассматриваемого года.
Решение. Очевидно, искомая матрица Х является суммой двух данных матриц А и В, т.е.
45 |
35 |
51 |
40 |
38 |
30 |
70 |
60 |
80 |
91 |
68 |
130 |
Х = К + В = 30 |
20 |
45 |
40 |
48 |
40 |
60 |
50 = |
50 |
85 |
88 |
110 |
50 |
45 |
48 |
45 |
51 |
50 |
58 |
52 |
95 |
93 |
101 |
110 . |
3. Вычитание матриц
Разность двух матриц одинакового размера определяется через операцию сложения матриц и умножения матрицы на число: К-В=К+(-1) В
4. Умножение матриц
Матрицу К можно умножить на матрицу В только в том случае, когда число столбцов матрицы К равно числу строк матрицы В.
63

Произведением матриц K |
B называется матрица |
m |
s s n |
которой cij, равен сумме произведений элементов i-й соответствующие элементы j-го столбца матрицы В, т.е.
Сm n, каждый элемент
строки матрицы К, на
s |
|
|
|
|
|
cij=кi1 b1j+кi2 b2j+кi3 b3j+…+кis bsj= |
kiq bqj , где i 1, m; j 1, n . |
||||
q |
1 |
|
|
|
|
5. Транспонирование матриц
Транспонированием матрицы называется замена строк матрицы на столбцы с сохранением их прядка. Пусть дана исходная матрица А:
|
a11 |
a12 |
... |
a1n |
|
A |
a21 |
a22 |
... |
a2n |
|
... ... ... ... |
|||||
|
|||||
|
am1 |
am2 |
... |
amn . |
|
Тогда транспонированная матрица АТ к матрице А имеет вид :
|
a11 |
a21 |
... |
am1 |
Т |
a12 |
a22 |
... |
am2 |
A |
... ... ... ... |
|||
|
||||
|
|
|
|
. |
|
a1n |
a2n |
... |
amn |
Пример 3. Магазином в течение дня в розницу продано 45, 30 и 50 единиц трёх видов товаров, соответственно по ценам 1; 2; 0,5 (тыс. руб.). Вычислить дневную выручку от розничной продажи всех видов товаров.
Решение. Представим данные о проданных товарах как |
матрицу |
||
|
|
|
1 |
K = 45 30 50 , а соответствующие цены (тыс.руб.) как матрицу P = 2 |
|||
1 |
3 |
3 |
1 |
|
|
|
0,5 |
Тогда искомую выручку U можно записать как произведение матриц К и Р, т.е.
1
U = K Р = (45 30 50) · 2 =45 1+30 2+50 0,5=130 (тыс. руб.).
0,5
Следовательно, дневная выручка магазина от розничной продажи товара, составляет 130 (тыс. руб.).
64

Пример 4. Предположим, что указанный в предыдущем примере магазин, кроме розничных, осуществляет также продажи оптовые на ярмарке и по линии посылторга. Данные о продажах за 1 день каждого вида товара записаны в таблице.
Вид продаж |
|
Вид товаров |
|
|
Костюм |
Пальто |
Платье |
Розничная |
45 |
30 |
50 |
Оптовая |
38 |
25 |
40 |
Посылторг |
20 |
15 |
20 |
|
|
|
|
Цена одной |
1 (тыс. руб.) |
2 (тыс. руб.) |
0,5 (тыс. руб.) |
ед. товара |
|
|
|
Требуется подсчитать дневную выручку от продаж (розничной, оптовой, посылторговской) каждого вида по отдельности. Выполнять эти вычисления с помощью матричной алгебры.
Решение. Данные о продажах (в штуках) некоторого магазина за один день запишем в виде матрицы:
45 30 50 А = 38 25 40 ,
20 15 20
где в строках указаны количества (в шт.) товара по видам продаж (розничная, оптовая и посылторговская), а в столбцах – количество (в шт.) по видам товаров (костюм, пальто, платье).
1
Данные о ценах (в тыс. руб.) записаны матрицей-столбцом Р= 2 ,
0,5
элементы которой являются ценами соответственно первого, второго и третьего (костюма, пальто, платья) видов товаров.
Искомые дневные выручки U1, U2, U3 продажи каждого из трёх видов товара можно записать в виде матрицы-столбца U и определить эту матрицу как произведение матриц А и Р следующим образом:
U1 |
|
45 |
30 |
50 |
1 |
45 |
1 |
30 |
2 |
50 |
0,5 |
130 |
U = U2 |
A P |
38 |
25 |
40 |
2 |
38 1 |
25 |
2 |
40 |
0,5 |
108 . |
|
U3 |
|
20 |
15 |
20 |
0,5 |
20 |
1 |
15 |
2 |
20 |
0,5 |
60 |
Дневные выручки от продажи первого, второго и третьего видов товара составляют соответственно:130, 108 и 60 (тыс. руб.).
65

Пример 5. Имеется 4 предприятия, выпускающие 3 вида изделий 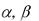
 ɣ и использующие при производстве 2 вида сырья. В таблице приведены данные о дневной производительности предприятий по каждому изделию, о затратах сырья на ед. изделия , о числе дней работы каждого предприятия и стоимости ед. сырья каждого вида.
ɣ и использующие при производстве 2 вида сырья. В таблице приведены данные о дневной производительности предприятий по каждому изделию, о затратах сырья на ед. изделия , о числе дней работы каждого предприятия и стоимости ед. сырья каждого вида.
|
Производительность шт./день |
|
Затраты кг/шт. |
|
|||
Изделие |
1 |
2 |
3 |
4 |
I |
|
II |
|
7 |
10 |
3 |
0 |
5 |
|
12 |
|
|
|
|
|
|
|
|
|
5 |
7 |
2 |
0 |
10 |
|
4 |
|
|
|
|
|
|
|
|
ɣ |
0 |
4 |
8 |
4 |
6 |
|
8 |
|
Количество рабочих дней в году |
Цены ед. сырья |
|||||
|
|
|
|
|
|
|
|
|
100 |
120 |
50 |
200 |
30 |
|
20 |
Требуется определить:
1)cуммарную производительность (за весь рабочий период) каждого предприятия по каждому из изделий.
2)количество каждого вида сырья, необходимого на каждом предприятии и для всех четырех предприятий.
3)размеры кредитов, которые необходимо предоставить всем предприятиям на закупку сырья.
Решение. Запишем условие задачи в матричном виде. Пусть матрица А – матрица производительности, В – матрица затрат сырья , матрица С – матрица цен на сырье, Т – матрица времени работы каждого из предприятий
|
7 |
5 |
0 |
5 |
12 |
|
|
|
100 |
0 |
0 |
0 |
|
10 |
7 |
4 |
|
30 |
|
0 |
120 |
0 |
0 |
||
А= |
; В= 10 |
4 |
; C = |
; Т = |
||||||||
|
3 |
2 |
8 |
6 |
8 |
|
20 |
|
0 |
0 |
50 |
0 |
|
0 |
0 |
4 |
|
|
|
0 |
0 |
0 |
200 . |
||
|
|
|
|
|
|
1. Суммарная производительность (за весь рабочий период) каждого предприятия по каждому из изделий будет равна:
|
100 |
0 |
0 |
0 |
7 |
5 |
0 |
|
700 |
500 |
0 |
|
Т А = |
0 |
120 |
0 |
0 |
10 |
7 |
4 |
= |
1200 |
840 |
480 |
|
|
0 |
0 |
50 |
0 |
3 |
2 |
8 |
|
150 |
100 |
400 |
|
|
0 |
0 |
0 |
200 |
0 |
0 |
4 |
|
0 |
0 |
800 |
. |
66

2. Расход сырья на каждом предприятии найдем из выражения:
|
700 |
500 |
0 |
5 |
12 |
|
8500 |
10400 |
|
|
1200 |
840 |
480 |
|
17280 |
21600 |
|
||
D= (Т А) В = |
10 |
4 |
= |
|
|||||
|
150 |
100 |
400 |
6 |
8 |
|
4150 |
5400 |
|
|
0 |
0 |
800 |
|
4800 |
6400 |
|
||
|
|
|
|
. |
Суммарное количество I и II видов сырья по всем предприятиям можно получить, умножив матрицу – строку L = (1 1 1 1) на матрицу D
|
|
8500 |
10400 |
|
M = L D = (1 1 1 1) · |
|
1720 |
21600 |
= (34 730 43 800 ). |
|
4150 |
5400 |
||
|
|
|
||
|
|
4800 |
6400 |
|
3. Чтобы найти размеры |
кредитов |
определяются стоимостью сырья, |
||
используемого каждым предприятием, умножим матрицу М на матрицу С. |
||||
Р = М С = (34 730 43 800) · |
30 |
= 1 041 900 + 876 000 = 1 917 900. |
||
|
20 |
|
|
|
Таким образом, размер кредитов всем предприятиям равен 1 917 900 руб.
Пример 6. В таблице приведены данные о дневной производительности пяти предприятий, выпускающих четыре вида продукции с потреблением трёх видов ресурсов, а также количество рабочих дней в году каждого предприятия и цены каждого вида сырья:
Вид |
|
Производительность |
|
Затраты ресурсов, |
|||||||
продукции |
предприятий (изд. в день) |
|
ед. веса/изд. |
||||||||
|
1 |
|
2 |
3 |
4 |
|
5 |
1 |
|
2 |
3 |
1 |
4 |
|
5 |
3 |
6 |
|
7 |
2 |
|
3 |
4 |
2 |
0 |
|
2 |
4 |
3 |
|
0 |
3 |
|
5 |
6 |
3 |
8 |
|
15 |
0 |
4 |
|
6 |
4 |
|
4 |
5 |
4 |
3 |
|
10 |
7 |
5 |
|
4 |
5 |
|
8 |
6 |
|
Кол-во раб. дней в году |
Цены ед. сырья |
|||||||||
|
200 |
|
150 |
170 |
120 |
|
140 |
40 |
|
50 |
60 |
Требуется найти:
67

1)годовую производительность каждого предприятия по каждому виду продукции;
2)годовую потребность каждого предприятия по каждому виду ресурса;
3)годовую сумму кредитования каждого предприятия для закупки ресурсов, необходимых для выпуска продукции указанных видов и при определённом количестве рабочих дней.
Решение: Введём следующие обозначения.
|
4 |
5 |
3 |
6 |
7 |
|
А= |
0 |
2 |
4 |
3 |
0 |
|
|
8 |
15 |
0 |
4 |
6 |
|
|
3 |
10 |
7 |
5 |
4 |
. |
Данная матрица является матрицей производительности пяти предприятий по всем 4 видам продукции. Каждый столбец этой матрицы соответствует дневной производительности отдельного предприятия по каждому виду изделий.
Следовательно, годовая производительность к-го предприятия по каждому виду изделий получается умножением к-го столбца матрицы А на количество рабочих дней в году для этого предприятия (к = 1,2,3,4,5) и описывается матрицей:
|
|
200 |
4 |
150 |
5 |
170 |
3 |
120 |
6 |
140 |
7 |
|
800 |
750 |
510 |
720 |
980 |
|
А1 |
= |
200 |
0 |
150 |
2 |
170 |
4 |
120 |
3 |
140 |
0 |
= |
0 |
300 |
680 |
360 |
0 |
|
200 |
8 |
150 15 |
170 |
0 |
120 |
4 |
140 |
6 |
1600 |
2250 |
0 |
480 |
840 |
|
||||
|
|
|
|
|||||||||||||||
|
|
200 |
3 |
150 10 |
170 |
7 |
120 |
5 |
140 |
4 |
|
600 |
1500 |
1190 |
600 |
560 |
. |
|
Матрица затрат сырья на ед. каждого вида продукции имеет вид:
2 3 4 5 S = 3 5 4 8
4 6 5 6 .
Дневной расход по видам ресурсов произведением матрицы S на матрицу А.
2 |
3 |
4 |
5 |
4 |
5 |
3 |
6 |
7 |
|
0 |
2 |
4 |
3 |
0 |
|||||
S∙A = 3 |
5 |
4 |
8 |
||||||
8 |
15 |
0 |
4 |
6 |
|||||
4 |
6 |
5 |
6 |
||||||
3 |
10 |
7 |
5 |
4 |
|||||
|
|
|
|
на |
предприятиях |
описывается |
|||
|
55 |
126 |
53 |
62 |
58 |
= |
68 |
165 |
85 |
89 |
77 |
|
74 |
167 |
78 |
92 |
82 . |
68

Для того чтобы найти годовую потребность каждого предприятия по каждому виду ресурсов, нужно к-й столбец матрицы (S∙A) умножить на количество рабочих дней в году для этого предприятия.
Следовательно, годовая потребность каждого предприятия по каждому виду ресурсов описывается матрицей
С = |
200 |
55 |
150 |
126 |
170 |
53 |
120 |
62 |
140 |
58 |
|
||
200 |
68 |
150 |
165 |
170 |
85 |
120 |
89 |
140 |
77 |
; |
|||
|
|||||||||||||
|
200 |
74 |
150 |
167 |
170 |
78 |
120 |
92 |
140 |
82 |
|
||
|
|
11000 |
18900 |
9010 |
7440 |
|
8120 |
|
|
||||
С= 13600 24750 14450 10680 10780 14800 25050 13260 11040 11480 .
Вектор стоимости ресурсов обозначим матрицей Р = (40 50 60). Следовательно, стоимость годового запаса ресурсов для каждого предприятия, получается умножением матрицы Р на матрицу С, т.е.
11000 18900 9010 7440 8120
Q = Р∙С = (40 50 60) · 13600 24750 14450 10680 10780 = 14800 25050 13260 11040 11480
= (2008000 3496500 1878500 1494000 1552600).
Суммы кредитования предприятия для закупки сырья определяется соответствующими элементами матрицы Q, т.е. q1=2 008 000; q2=3 496 500; q3=1 878 500; q4=1 494 000; q5=1 552 600.
7.4. Системы линейных уравнений. К системам линейных уравнений приводит множество задач, связанных с экономикой.
Система m-линейных уравнений с n неизвестными – это система вида:
a11x1 |
a12 x2 |
... |
a1n xn |
b1, |
a21x1 |
a22 x2 |
... |
a2n xn |
b2 , |
am1x1 |
am2 x2 |
... |
amn xn |
bm . |
69

|
n |
|
|
|
Сокращенная запись системы |
aij x |
j |
bi , |
|
|
j |
1 |
|
|
где аij – коэффициенты при |
неизвестных , |
bi – свободные члены системы |
||
уравнений ( i=1, 2…m; j=1, 2, |
…n). |
|
|
|
Решением системы называется совокупность n чисел ( х1=к1, х2 =к2, ...хn=кn) при которых каждое уравнение системы обращается в верное равенство.
Система уравнений называется совместной, если она имеет хотя бы одно решение, и несовместной, если она не имеет решений.
Совместная система уравнений называется определённой, если она имеет единственное решение, и неопределённой, если она имеет более одного решения.
Две системы называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Запишем систему уравнений в матричной форме
|
a11 |
a12 |
... |
a1n |
; |
|
x1 |
, |
|
b1 |
, |
A |
a21 |
a22 |
... |
a2n |
X |
x2 |
B |
b2 |
|||
... ... ... ... |
|
... |
|
... |
|
||||||
|
|
|
|
|
|
||||||
|
am1 |
am2 |
... |
amn |
|
|
xn |
|
|
bm |
|
где А ‒ матрица коэффициентов при переменных, или матрица системы; |
|||||||||||
Х ‒ матрица – столбец переменных; |
В ‒ матрица – столбец свободных |
||||||||||
членов систем. |
|
|
|
|
|
|
|
|
|
||
Тогда система уравнений примет вид: А∙Х=В.
Рассмотрим частный случай системы, когда число уравнений равно числу неизвестных m=n . Тогда матрица системы является квадратной. Допустим, что
квадратная матрица невырожденная, т.е. её определитель |
. В этом случае |
||||||
существует |
обратная матрица |
, такая, что Х=А-1∙В. |
Элементы обратной |
||||
матрицы можно рассчитать по формуле |
|
||||||
|
|
|
A11 |
A21 .. |
An1 |
|
|
|
1 |
A |
A .. |
A |
, |
|
|
A 1 |
|
|
12 |
22 |
n2 |
|
|
|
A |
|
.. .. .. .. |
|
|
||
|
|
|
|
|
|
||
|
|
|
A1n |
A2n .. |
Ann |
|
|
где Аij – алгебраическое дополнение элемента aij , Аij =(-1)i+j∙Mij,,
70

Mij – минор – определитель, полученный из определителя матрицы системы вычеркиванием i-строки и j-го столбца.
Пример 7. Затраты трёх видов сырья (А; В; С) на производство каждого из трех видов продукции (1, 2, 3) и запасы каждого вида сырья даны в таблице
Вид |
Затраты сырья на 1 ед. |
Запас сырья |
|||
продукции |
|
продукции |
|
|
|
Вид сырья |
|
|
|
|
|
|
|
|
|
|
|
А |
2 |
3 |
|
1 |
245 |
В |
1 |
0 |
|
2 |
130 |
С |
3 |
4 |
|
0 |
270 |
Требуется определить план производства, обеспечивающий использование всего сырья.
Решение. Пусть предприятие выпустит 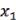 ед. продукции 1-го вида,
ед. продукции 1-го вида,  ед. продукции 2-го вида,
ед. продукции 2-го вида, 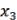 ед. продукции 3-го вида. Расход сырья А, на производство по такому плану, составит (2
ед. продукции 3-го вида. Расход сырья А, на производство по такому плану, составит (2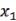 +3
+3  +
+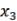 ) ед., что по условию, должно равняться его запасу, т.е. 2
) ед., что по условию, должно равняться его запасу, т.е. 2 +3
+3 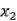 +
+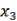 =245. Аналогично, приравнивая расходы и запасы сырья В и С, приходим к системе уравнений:
=245. Аналогично, приравнивая расходы и запасы сырья В и С, приходим к системе уравнений:
2x1 3x2 x3 245, x1 2x3 130,
3x1 4x2 270.
Решим полученную систему матричным способом, решение имеет вид
Х=А-1∙В.
Введем обозначения
матрица системы; |
матрица свободных членов |
матрица неизвестных |
|
|
|
|
|
|
|
Вычислим обратную матрицу по формуле А-1= |
|
1 |
|
· |
А11 |
А21 |
А31 . |
|
|
|
|
|
|||
|
|
А |
|
|
А12 |
А22 |
А32 |
|
|
|
|
|
А13 |
А23 |
А33 |
71
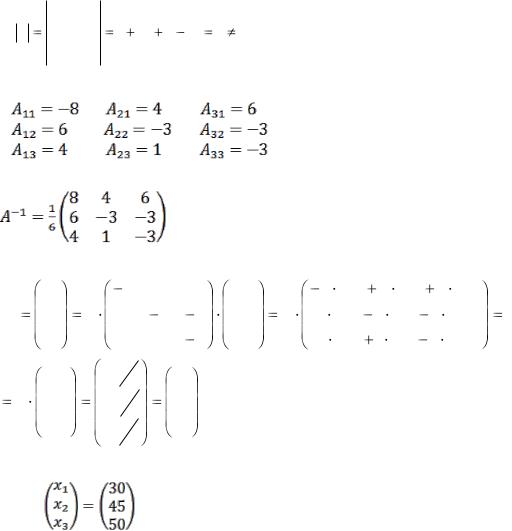
2 3 1
A 3 0 2 0 18 4 16 6 0. . 1 4 0
, тогда
|
|
x1 |
1 |
8 |
4 |
6 |
245 |
1 |
8 |
245 |
4 130 |
6 |
270 |
X |
|
x2 |
6 |
3 |
3 |
180 |
6 245 |
3 130 |
3 270 |
||||
|
|
|
|||||||||||
|
6 |
6 |
|||||||||||
|
|
x3 |
4 |
1 |
3 |
270 |
4 |
245 |
1 130 |
3 270 |
|||
|
|
|
|
||||||||||
|
|
180 |
|
180 |
|
30 |
|
|
|
|
|
|
|
|
1 |
|
6 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
270 |
|
270 |
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
6 |
|
6 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
300 |
|
300 |
|
50 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
X= |
|
. |
|
|
|
|
|
|
|
|
|
|
Итак, предприятие при сбалансированном плане должно выпускать 30 ед. продукции первого вида, 45 ед. продукции второго вида и 50 ед. продукции третьего вида.
Пример 8. На предприятие, с работниками четырёх категорий, привезли заработную плату в купюрах следующего достоинства: по 100 руб. -1 850, по 50 руб. - 230, по 10 руб. – 250, по 1 руб. – 740. Заработная плата работника 1-й
категории составляет 962 |
руб.; 2-й категории – 713 руб.; 3-й категории – |
452 руб.; 4-й категории ‒ |
261 руб. Определить, сколько сотрудников каждой |
категории работает на предприятии, если каждому сотруднику выдали заработную плату минимальным числом купюр.
Решение: условие об оплате минимальным числом купюр является основным в определении количества купюр разного достоинства, выданных сотрудникам разных категорий. Исходя из величины заработной платы по категориям однозначно определяем все виды распределения купюр.
72

Если 1-й категории получает зарплату в размере 962 руб., то ему выдают 9 купюр достоинством 100 руб.; 1 купюру достоинством 50 руб.; 1 купюру достоинством 10 руб. и 2 купюры достоинством 1 руб. составим таблицу распределения купюр по категориям.
Достоинство |
|
Распределение купюр по категориям |
Общее кол- |
|||
купюр в руб |
1 |
|
2 |
3 |
4 |
во купюр |
100 |
9 |
|
7 |
4 |
2 |
1850 |
50 |
1 |
|
- |
1 |
1 |
230 |
10 |
1 |
|
1 |
- |
1 |
250 |
1 |
2 |
|
3 |
2 |
1 |
740 |
Если  , – это соответствующее количество работников каждой категории , тогда 9
, – это соответствующее количество работников каждой категории , тогда 9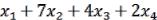 – количество купюр достоинством 100 руб, выданных работникам всех категорий. Так как этих купюр всего 1 850, то можно составить уравнение
– количество купюр достоинством 100 руб, выданных работникам всех категорий. Так как этих купюр всего 1 850, то можно составить уравнение
9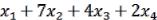 =1 850
=1 850
По аналогии составляем ёще три уравнения
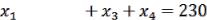 ;
;
 ;
;
Получим систему уравнений, которую можно решить различными способами. Уравнения в этой системе можно записать в разном порядке. Запишем ее так.
|
x1 |
x3 |
x4 |
230, |
|
|
x1 |
x2 |
x4 |
250, |
|
2x1 |
3x2 |
2x3 |
x4 |
740, |
|
9x1 |
7x2 |
|
4x3 |
2x4 |
1850. |
Решив систему, получили: х1=50, х2=120, х3=100, х4=80.
Ответ: Работников 1-й категории 50 человек, работников 2-й категории 120 человек, работников 3-й категории 100 человек, работников 4-й категории 80 человек.
7.5. Модель Леонтьева многоотраслевой экономики (балансовый метод)
Межотраслевой баланс производства и распределения продукции является одним из важнейших экономико-математических методов анализа и
73
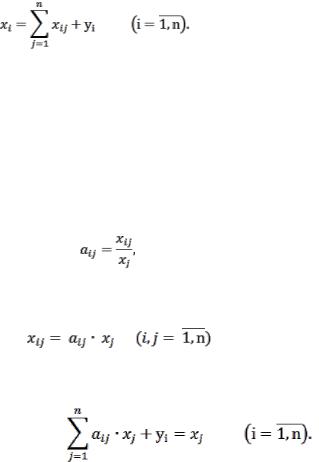
планирования экономических связей отраслей народного хозяйства. Цель балансового анализа – выяснить, каким должен быть объём производства, каждой из n отраслей, чтобы удовлетворить все потребности в продукции этой отрасли. При этом каждая отрасль выступает одновременно как производитель некоторой продукции, так и как потребитель продукции своей и другими отраслями.
Предположим, что рассматривается n отраслей материального производства, каждая из которых производит свою продукцию. Часть этой продукции идёт на внутрипроизводственное потребление самой отраслью и другими отраслями, а другая часть предназначена для конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства и распределения продукции за некоторый период времени (год):
Рассмотрим статический стоимостный баланс, когда все величины, входящие в уравнение, имеют стоимостное выражение.
При построении такой модели исходят из того, что объёмы производственного потребления прямо пропорциональны объёмам производства продукции потребляющих отраслей.
Коэффициентами пропорциональности являются коэффициенты прямых материальных затрат:
которые показывают затраты продукции i-ой отрасли на производство единицы валовой продукции j-й отрасли. Тогда
означает линейную зависимость материальных затрат от валового выпуска, вследствие чего построенная модель примет вид:
Обозначим
74
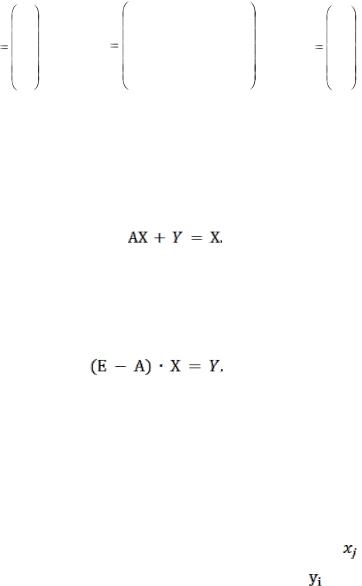
|
x |
|
a11 |
a11 |
.. |
a11 |
|
y |
|
|
1 |
; |
|
|
|
; |
|
1 |
, |
|
x2 |
a21 |
a22 |
.. |
|
y2 |
|||
X |
A |
a2n |
Y |
|
|||||
.. |
|
.. .. .. .. |
.. |
|
|||||
|
|
|
|
|
|||||
|
xn |
|
am1 |
am1 |
.. |
amn |
|
yn |
|
где Х – матрица столбец валового выпуска продукции, А – матрица коэффициентов прямых материальных затрат, Y – матрица столбец конечной продукции.
Тогда математическую модель МОБ можно записать в матричном виде
Основная задача МОБ состоит в том, чтобы отыскать такой вектор валового выпуска Х, который, при известной матрице прямых материальных затрат А, обеспечивает заданных вектор конечного продукта Y.
Из предыдущего уравнения следует:
Если матрица (Е – А) невырожденная, т.е.  , то для неё можно найти обратную матрицу , тогда Х найдем из уравнения
, то для неё можно найти обратную матрицу , тогда Х найдем из уравнения
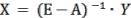 .
.
Матрица 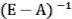 =В называется матрицей коэффициентов полных материальных затрат, элементы которой показывают потребность в валовом выпуске продукции отрасли i для производства единицы конечной продукции в
=В называется матрицей коэффициентов полных материальных затрат, элементы которой показывают потребность в валовом выпуске продукции отрасли i для производства единицы конечной продукции в
отрасли j. В соответствии с экономическим смыслом, значения |
|
должны быть |
неотрицательными при неотрицательных значениях |
и |
аij ≥ 0, |
где (i ,j=1,2 , ...n). |
|
|
Рассмотрим конкретный пример задачи, для которой необходимо составить математическую модель и ответить на поставленный в ней вопрос.
Пример 9. Предприятие состоит из трёх цехов, каждый из которых выпускает один вид продукции. Прямые затраты  единицы продукции i-го цеха, используемые как сырьё (промежуточный продукт) для выпуска единицы продукции j-го цеха, а также количество единиц конечной продукции i-го цеха, предназначенный для реализации, представлены в таблице:
единицы продукции i-го цеха, используемые как сырьё (промежуточный продукт) для выпуска единицы продукции j-го цеха, а также количество единиц конечной продукции i-го цеха, предназначенный для реализации, представлены в таблице:
Продукция |
|
Прямые затраты |
Конечный |
||
цехов |
1 |
|
2 |
3 |
продукт |
1-го |
0 |
|
0,2 |
0 |
200 |
2-го |
0,2 |
|
0 |
0,1 |
100 |
3-го |
0 |
|
0,1 |
0,2 |
300 |
|
|
75 |
|
|
|

Определить: а) коэффициенты полных затрат; б) валовый выпуск продукции для каждого цеха; в) производственную программу; г) коэффициенты косвенных затрат.
Решение. Обозначим производственную программу предприятия через
x1
Xx2 , где  валовый выпуск продукции 1, 2, 3 цехов, x3
валовый выпуск продукции 1, 2, 3 цехов, x3
y1
y2 – план выпуска конечной продукции (товарной). y3
0 0,2 0
A 0,2 0 0,1 (aij ) 0 0,1 0,2
Производственные взаимосвязи предприятия представлены следующей системой трёх уравнений
0 |
x1 |
0,2 x2 |
0 x3 |
200 |
x1, |
0,2x1 |
0 x2 |
0,1x3 |
100 |
x2 , |
|
0 |
x1 |
0,1x2 |
0,2x3 |
300 |
x3. |
В матричном виде система примет вид |
|
|
|
или |
, |
||||
где |
|
= В – матрица полных затрат, тогда |
|
|
|
||||
а) для решения системы найдем сначала |
|
, а затем |
= В. |
||||||
|
|
0 |
0,2 |
0 |
1 |
0 |
0 |
|
|
Е |
А |
0,2 |
0 |
0,1 , где Е |
0 |
1 |
0 |
– единичная матрица. |
|
|
|
0 |
0,1 |
0,8 |
0 |
0 |
1 |
|
|
Вычислим
Найдём алгебраические дополнения элементов этой матрицы.
А11=0,79 А21=0,16 А31=0,02 А12=0,16 А22=0,8 А32=0,1 А13=0,02 А23=0,1 А33=0,96,
76

|
1 |
0,79 |
0,16 |
0,02 |
1,04 |
0,21 |
0,03 |
|
тогда (Е-А)-1 = В = |
0,16 |
0,8 |
0,1 |
0,21 |
1,05 |
0,13 . |
||
0,758 |
||||||||
|
0,02 |
0,1 |
0,96 |
0,3 |
0,13 |
1,27 |
Это матрица коэффициентов полных материальных затрат.
1,04 |
0,21 |
0,03 |
200 |
238 |
б) Х = 0,21 |
1,05 |
0,13 |
100 |
186 , т.е. валовый выпуск продукции 1-го, |
0,03 |
0,13 |
1,21 |
300 |
400 |
2-го и 3-го цехов будут соответственно x1=238, x2=186, x3=400.
в) Найдём производственную программу каждого цеха (промежуточный
|
|
|
|
||||||
продукт) по формуле хij = aij ∙ xij , (i=1,3 , j= 1,3 ) |
|
||||||||
х11=а11х1 |
= 0 |
238=0; |
х12=а12х2 |
= 0,2 186 = 37,2 |
37; |
||||
х13=а13х3 |
= 0 |
400 = 0; |
х21=а21х1 = 0,2 238 = 47,6 |
48; |
|||||
х22=а22х2 |
= 0 |
186 = 0; |
х23=а23х3=0,1 400 = 40; |
|
|||||
х31=а31х1 |
= 0 |
238 = 0; |
х32=а32х2 |
= 0,1 186 = 18,6 |
19; |
||||
х33=а33х3 = 0,2 400 = 80.
В результате получим следующую таблицу:
Цех |
Внутрипроизводственные |
Итого |
Конечный |
Валовый |
||||
|
|
потребления |
|
|
продукт |
выпуск |
||
|
1 |
|
2 |
|
3 |
|
|
|
1 |
0 |
|
37 |
|
0 |
37 |
200 |
237 |
2 |
48 |
|
0 |
|
40 |
88 |
100 |
186 |
3 |
0 |
|
19 |
|
80 |
99 |
300 |
400 |
г) Коэффициенты косвенных затрат сij определяются как разности полных внутрипроизводственных затрат bij и прямых затрат аij. В матричной форме:
1,04 |
0,21 |
0,03 |
0 |
0,2 |
0 |
|
1,04 |
0,01 |
0,03 |
С = В – А = 0,21 |
1,05 |
0,13 |
0,2 |
0 |
0,1 |
; С = |
0,01 |
1,05 |
0,03 . |
0,03 |
0,13 |
1,27 |
0 |
0,1 |
0,2 |
|
0,03 |
0,03 |
1,07 |
77

ЗА Д А Ч И
1.Пусть некоторая фирма осуществляет продажи: розничные, оптовые, продажи за рубежом. Данные за год о продажах (в усл. ед.) записаны в виде матрицы
60 30 10 А = 50 60 15 ,
1 2 4
при этом в строках указаны объёмы товаров по видам продаж (розничная, оптовая, продажи за рубежом), а в столбцах – по видам товара (три вида товара).
1
Данные о ценах (в ден. ед.) заданы матрицей Р = 2 , элементы которой
3
являются ценами соответственно 1-го, 2-го и 3-го видов товара. Вычислить выручку за год от продажи каждого вида товара.
2. Два предприятия выпускают три типа мебельных гарнитуров, расходуя при этом четыре вида сырья: фанеру, пластмассу, ткань, древесину. Нормы материальных затрат заданы для каждого предприятия матрицами А и В соответственно
2 |
1 |
5 |
0 |
2 |
3 |
|
|
|
|
|
|||
0 |
4 |
3 |
4 |
1 |
5 |
|
А= 2 |
7 |
1 |
, В= 6 |
0 |
2 |
. Первое предприятие выпустило 100 гарнитуров |
3 |
2 |
8 |
7 |
3 |
1 |
|
1-го типа, 100 – 2-го типа и 0 – 3-го типа, а второе предприятие – соответственно 300, 200 и 100. Найти матрицу полных затрат.
3. В городе имеются три ателье индивидуального пошива женского лёгкого платья 1-го, 2-го и 3-го разрядов. Каждое ателье изготовляет 4 вида изделий – юбки, платья, блузки, брюки. Найти матрицу поквартальной выручки ателье (Т), если матрица расценок D и матрица поквартального плана Р имеют вид
15 |
45 |
20 |
20 |
|
35 |
30 |
40 |
30 |
|
|
30 |
25 |
20 |
20 |
|
||||
D = 20 |
50 |
25 |
25 |
|
|
||||
, Р = |
30 |
35 |
40 |
30 |
. |
||||
25 |
60 |
30 |
30 |
|
|
||||
|
20 |
18 |
15 |
20 |
|
||||
|
|
|
|
|
|
||||
|
|
|
78 |
|
|
|
|
|
|

Матрица поквартальной выручки определяется как произведение матрицы расценок D на матрицу поквартального плана Р , т.е. (Т=D Р).
4. Три предприятия используют два вида сырья: уголь и древесину. Заданы
10 20
матрицы расхода сырья Х= 50 0 и матрица стоимостей перевозок тремя
30 10
3 5 8
видами транспорта Р= 7 2 8 . Определить матрицу затрат по видам транспорта Y=X P.
5. Для изготовления трёх типов игрушек необходимы детали в следующих количествах:
Вид детали |
|
Тип игрушки |
|
||
|
1 |
|
2 |
|
3 |
I |
4 |
|
6 |
|
8 |
II |
2 |
|
2 |
|
3 |
III |
1 |
|
1 |
|
1 |
1)записать в виде матричного соотношения зависимость необходимых деталей каждого вида от количества изготавливаемых игрушек;
2)используя обратную матрицу, записать выражение количества изготовленных игрушек через количество израсходованных деталей;
3)сколько нужно деталей каждого вида для изготовления 3 игрушек 1-го типа, 2 игрушек 2-го типа, 1 игрушки 3-го типа?
4)сколько было изготовлено игрушек каждого типа, если было истрачено 90 деталей 1-го вида, 35 – 2-го вида, 15 – 3-го вида?
6. Два цеха предприятия выпускают продукцию двух видов: первый цех – продукцию 1-го вида, второй – продукцию 2-го вида. Часть выпускаемой продукции идёт на внутреннее потребление, остальная часть является конечным продуктом. Требуется выявить распределение между цехами продукции, идущей на внутреннее потребление, и общие (валовые) объёмы выпускаемой продукции,
79

если заданы параметры прямых затрат А=(аij) и конечного продукта (yj):
|
1 |
1 |
|
|
|
||
|
|
|
|
|
|
|
130 . |
А= |
5 |
10 |
, Y= |
||||
|
1 |
|
1 |
|
|
190 |
|
45
7.Обувная фабрика специализируется по выпуску изделий трёх видов – сапог, кроссовок и ботинок; при этом используется сырьё трёх типов: S1, S2, S3. Нормы расхода каждого из них на одну пару обуви и объём расхода сырья на 1 день заданы таблицей:
Вид |
Нормы расхода сырья на одну |
Расход |
|||
сырья |
|
пару, усл.ед. |
|
сырья на 1 |
|
|
|
|
|
|
день, усл.ед. |
|
сапоги |
кроссовки |
|
ботинки |
|
S1 |
5 |
3 |
|
4 |
2 700 |
S2 |
2 |
2 |
|
1 |
800 |
S3 |
3 |
1 |
|
2 |
1 600 |
Найти ежедневный объём выпуска каждого вида обуви.
8. В таблице приведены данные об исполнении баланса за отчётный период, у.д.ед.:
Производство |
|
Потребление |
Конечный |
Валовый |
|
|
|
|
|
продукт |
продукт |
|
|
|
|
|
|
|
|
1 |
2 |
|
|
Отрасль |
1 |
100 |
160 |
240 |
500 |
|
2 |
275 |
40 |
85 |
400 |
Вычислить необходимый объём валового выпуска каждой отрасли, если конечный продукт первой отрасли должен увеличится в 2 раза, а второй отрасли
– на 20%.
8. ЗАДАЧИ ЛИНЕЙНОГО ПРОГРАММИРОВАНИЯ
Задачи, в которых находится максимум или минимум некоторой функции при наличии ограничений, объединяются общим названием – задачи математического программирования.
80
Линейное программирование – это один из разделов математического оптимального программирования, изучающий способ отыскания максимума или минимума линейной функции при наличии линейных ограничений. При этом линейная функция называется целевой функцией. Перечень переменных, при которых целевая функция достигает max или min, определяет оптимальный план, а всякий другой набор переменных, удовлетворяющий системе ограничений, определяет допустимый план.
Стандартная задача линейного программирования
Z c1x1 |
c2 x2 |
... |
cn xn |
|
max |
|
||
a11x1 |
a12 x2 |
... |
a1n xn |
b1, |
|
|
||
a21x1 |
a22 x2 |
... |
a2n xn |
b2 |
, |
(7.1) |
||
|
|
|
|
|
|
|
|
|
am1 x1 |
am2 x2 |
... |
amn xn |
|
bm . |
|
||
|
|
|
|
|
|
|
|
|
|
x j |
0; |
j 1, n. |
|
|
|||
Алгоритм симплексного метода
1.Записываем данную задачу в исходную симплексную таблицу.
2.Если все элементы оценочной строки симплексной таблицы неотрицательны, то соответствующий план является оптимальным.
3.Если в оценочной строке содержится отрицательный элемент, а в столбце над ним нет ни одного положительного элемента, то целевая функция не ограничена сверху на множестве допустимых планов и задача не имеет решения.
4.Если в каждом столбце соответствующем отрицательной оценке содержится хотя бы один положительный элемент, то можно перейти к “лучшему ” плану следующим образом:
а) выбираем разрешающий столбец по наименьшей отрицательной оценке;
б) выбираем разрешающую строку по минимальному значению ;
 равно отношению свободных членов к соответствующим положительным элементам разрешающего столбца; в) на пересечении разрешающего столбца и разрешающей строки лежит разрешающий элемент;
равно отношению свободных членов к соответствующим положительным элементам разрешающего столбца; в) на пересечении разрешающего столбца и разрешающей строки лежит разрешающий элемент;
г) элементы разрешающей строки делим на разрешающий элемент и записываем в новой таблице, сохраняя порядок строки, оставшиеся элементы разрешающего столбца заполняем нулями;
81

д) элементы остальных строк, в том числе и оценочной строки, вычисляем по формулам прямоугольников
aik |
|
aip |
|
|
aqp |
aik aqk |
aip |
|
|||
|
|
|
|
|
|
aik |
|
||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
aqp |
|
. |
(7.2) |
|
aqk |
|
|
|
aqp |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 1. Задача выпуска продукции. Для изготовления трех видов продукции (А; Б; В) используются три вида сырья (S1, S2, S3). Запасы сырья , нормы его расхода на единицу продукции, цена реализации единицы продукции каждого вида заданы в следующей таблице
Вид сырья |
Нормы расхода сырья на 1ед. продукции |
Запас сырья |
||
|
|
|
|
|
|
А |
Б |
В |
|
|
|
|
|
|
S1 |
7 |
0 |
5 |
220 |
|
|
|
|
|
S2 |
2 |
3 |
2 |
140 |
S3 |
5 |
1 |
1 |
100 |
Цена ед. прод. |
2 |
1 |
1 |
|
|
|
|
|
|
Определить оптимальный план выпуска продукции, при котором выручка от реализации выпущенной продукции будет максимальной. Составить математическую модель задачи, решить задачу симплексным методом.
Решение. |
|
|
|
|
|
|
|
Составим математическую модель. |
|
|
|
||||
Пусть предприятие выпустит x1 единиц – продукции А, х2 |
единиц – |
||||||
продукции Б, х3 единиц – продукции В. |
|
|
|
||||
Расход сырья S1 |
на все виды продукции – 7х 0 х2 |
5х3 . По условию задачи |
|||||
|
|
|
|
1 |
|
|
|
расход сырья S1 |
не должен превышать запаса 220, |
т.е. 7х 0 х |
2 |
5х ≤ 220 |
|||
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|
|
|
Аналогично составляем ограничения расхода сырья S2 и S3. Получим систему |
|||||||
|
7х1 |
0х2 |
5х3 |
220; |
|
|
|
неравенств: |
2x1 |
3x2 |
2x3 |
140; |
|
|
(7.3) |
|
|
|
|
||||
|
5x1 |
x2 |
x3 |
100. |
|
|
|
|
x1 |
0, x2 |
0, x3 0 |
|
|
|
|
|
|
|
|
82 |
|
|
|

Выручка от реализации выпущенной продукции будет равна |
|||||
Z |
2x1 |
x2 |
x3 |
max . |
(7.4) |
Введем балансовые переменные x4 , |
x5 , x6 в каждое неравенство для приведения |
||||
модели к каноническому виду |
|
||||
7x1 |
0x2 |
5x3 |
x4 |
220; |
|
2x1 |
3x2 |
2x3 |
x5 |
140; |
(7.5) |
5x1 |
x2 |
x3 |
x6 |
100. |
|
x j |
|
0 , (j=1,2,…6) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z 2x1 x2 |
x3 |
max . |
|
|
|
|
|
|
|
|
|
|
|
|
|
(7.6) |
|||||
|
Составим симплексную таблицу. |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Базис |
|
|
с1=2 |
с2= 1 |
|
с3=1 |
с4=0 |
с5=0 |
с6=0 |
|
|
|
|
|
|
|
|
||
cj |
|
xj |
ai0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
x2 |
|
x3 |
x4 |
x5 |
x6 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
|
x4 |
220 |
|
7 |
|
0 |
|
|
5 |
1 |
0 |
0 |
220/7 |
|
|
|||||
0 |
|
x5 |
140 |
|
2 |
|
3 |
|
|
2 |
0 |
1 |
0 |
140/2 |
|
|
|||||
0 |
|
x6 |
100 |
|
5 |
|
1 |
|
|
1 |
0 |
0 |
1 |
100/5 min |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
а00 =0 |
а01= |
а02 = |
|
а03 = |
а04= |
а05 =0 |
а06 =0 |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
-2 |
|
-1 |
|
|
-1 |
0 |
|
|
|
|
|
|
|
|
|
|
0 |
|
x4 |
80 |
|
0 |
|
-7/5 |
|
|
18/5 |
1 |
0 |
-7/5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
100 |
|
|
min |
|
||
0 |
|
x5 |
100 |
|
0 |
|
13/5 |
|
|
8/5 |
0 |
1 |
-2/5 |
5 /13 |
|
|
|||||
2 |
|
x1 |
20 |
|
1 |
|
1/5 |
|
|
1/5 |
0 |
0 |
1/5 |
20 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1/ 5 |
|
|
|
|
|
||
|
|
Z |
40 |
|
0 |
|
-3/5 |
|
|
-3/5 |
0 |
0 |
2/5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1740 |
min |
|
||||
0 |
|
x4 |
1740/13 |
0 |
|
0 |
|
|
58/13 |
1 |
7/13 |
-21/13 |
|
|
|||||||
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
58 |
|
|
|
|
|||||||||||||
1 |
|
x2 |
500/13 |
0 |
|
1 |
|
|
8/13 |
0 |
5/13 |
-2/13 |
|
|
|
|
|||||
|
|
|
|
500/8 |
|
|
|||||||||||||||
2 |
|
x1 |
160/13 |
1 |
|
0 |
|
|
1/13 |
0 |
-1/13 |
3/13 |
160 |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Z |
820/13 |
0 |
|
0 |
|
|
-3/13 |
0 |
3/13 |
4/13 |
|
|
|
|
|
|
|
|
|
1 |
|
x3 |
30 |
|
0 |
|
0 |
|
|
1 |
13/58 |
7/58 |
-21/58 |
|
|
|
|
|
|
|
|
1 |
|
x2 |
20 |
|
0 |
|
1 |
|
|
0 |
-8/58 |
18/58 |
4/58 |
|
|
|
|
|
|
|
|
2 |
|
x1 |
10 |
|
1 |
|
0 |
|
|
0 |
-1/58 |
-5/58 |
15/58 |
|
|
|
|
|
|
|
|
|
|
Z |
70 |
|
0 |
|
0 |
|
|
0 |
3/58 |
15/58 |
13/58 |
|
|
|
|
|
|
|
|
Таблица заполняется следующим образом:
Встолбце “ai0” записываются свободные члены уравнений (7.5), в столбцах
“x1”, “x2”, …, “x6” − коэффициенты при соответствующих неизвестных этой системы.
83

В столбце “базис” выписываются базисные переменные, содержащиеся в соответствующих уравнениях системы (7.5).
Верхняя строчка и крайний левый столбец содержат коэффициенты при соответствующих неизвестных целевой функции Z выражения (7.6).
Последняя строка таблицы называется оценочной строкой, а её элементы a0j оценками. Первый элемент a00 оценочной строки равен значению целевой функции Z для начального опорного плана X 0 (0,0,0,220,140,100) . Это значение может быть получено как результат скалярного умножения вектора – столбца “сj “ на вектор – столбец свободных членов “ai0”:
Z( X 0) = a00 = 0·220 + 0·140 + 0·100 = 0.
Остальные значения a0к оценочной строки получаются в результате скалярного умножения вектора – столбца “сj“ на вектор – столбец
коэффициентов при переменной хк с последующим вычитанием |
|||||
соответствующего элемента ск верхней строки: |
|
|
|||
a01 |
= 0·7 + 0·2 +0·5 – 2 = -2; |
|
|
||
a02 |
= 0·0 + 0·3 +0·1 – 1 = -1; |
|
|
||
a03 |
= 0·5 + 0·2 +0·1 – 1 = -1. |
|
|
||
Оценки для базисных переменных всегда равны 0. |
|
|
|||
|
|
|
|
|
|
Исходное опорное решение X 0 (0;0;0;220;140;100), Z0 0 |
не |
является |
|||
оптимальным, в оценочной строке три отрицательные оценки |
(-2), |
(-1), (-1), |
|||
ситуация соответствует пункту 4 алгоритма симплексного метода. |
Перейдём к |
||||||||||||
новому опорному плану: |
|
|
|
|
|
|
|||||||
а) разрешающий столбец соответствует переменной |
x1 , |
т.к. оценка (-2) ─ |
|||||||||||
наименьшая отрицательная оценка оценочной строки; |
|
|
|
|
|||||||||
б) |
третья |
строка |
является |
разрешающей, |
т.к. |
для |
неё |
||||||
min |
min |
220 |
; |
140 |
; |
100 |
|
min 31,4;70;20 |
20 ; |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
7 |
2 |
5 |
|
|
|
|
|
|
|
|||
в) на пересечении разрешающих столбца и строки лежит разрешающий элемент 5, при этом в базис войдёт переменная x1 , а переменная x6 выйдет из базиса;
г) элементы разрешающей строки делим на разрешающий элемент 5 и записываем полученные значения в третьей строке второй таблицы, оставшиеся элементы разрешающего столбца заполняем нулями; Остальные элементы таблицы 2 находим по правилу прямоугольника (7.2). Приведем расчёты некоторых из них:
84

a |
220 5 7 |
100 |
80 , a |
0 5 |
1 7 |
|
7 |
, a |
5 5 |
1 7 |
|
|
18 |
, |
|
|
|
||||||
10 |
5 |
|
|
12 |
|
|
5 |
|
5 |
13 |
|
|
|
|
5 |
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
a00 |
0 5 100 |
( 2) |
40, a02 |
|
5 ( |
1) ( 1) |
( 2) |
|
|
3 |
|
, |
a26 |
|
5 |
0 1 2 |
|
2 |
. |
||||
5 |
|
|
|
|
5 |
|
|
|
5 |
|
|
|
5 |
|
5 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
В |
результате |
первой |
|
итерации |
|
получим |
|
новое |
опорное |
|
решение |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X1(20;0;0;80;100;0) , Z1 |
40 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Вторая итерация приводит к решению: |
|
|
|
( |
160 |
; |
500 |
;0; |
1740 |
;0;0) , Z |
|
820 |
. |
|
|
|
||||||
|
|
X |
2 |
2 |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
13 |
13 |
13 |
|
|
|
|
13 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
После третьей итерации получаем оптимальное решение: |
X 3 (10;20;30;0;0;0) , |
|||||||||||||||||||||
Zm ax |
70 . Дальнейшее увеличение Z невозможно, |
т.к. все оценки оценочной |
||||||||||||||||||||||
строки стали неотрицательными. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
Оптимальное решение исходной задачи получаем отбрасыванием из |
|
|
|
|||||||||||||||||||
|
|
X 3 |
||||||||||||||||||||||
компонент, связанных |
с балансовыми |
|
|
переменными |
|
|
x4 , x5 , x6 , |
т.е. |
||||||||||||||||
|
|
|
(10,20,30) , при этом значение Zm ax |
|
70 не изменится. |
|
|
|
|
|
|
|
|
|
||||||||||
X опт |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Транспортная задача
В пунктах производства А1, А2 , А3 , Аm имеется однородный груз в количестве соответственно а1 , а2 , а3 , аm . Данный груз необходимо доставить в n пунктов назначения В1 , В2 … Вn в количестве соответственно b1 , b2 ,… bn . Стоимость перевозки единицы груза (тариф) из пункта Аi в пункт B j равна cij . Требуется составить план перевозок, при котором все грузы будут вывезены с минимальными затратами.
Модель задачи имеет вид :
m |
n |
|
|
Z |
cij xij |
min |
|
i 1 j |
1 |
|
|
n |
|
|
|
|
xij |
ai , |
i = 1, 2, …, m, |
j |
1 |
|
|
|
|
||
m |
|
|
|
|
xij |
bj , |
j = 1, 2, …, n, |
i |
1 |
|
|
|
xij |
0. |
|
85

|
m |
n |
Транспортная задача называется закрытой если |
ai |
b j . |
|
i 1 |
j 1 |
Чаще же возникают задачи, в которых это условие баланса нарушено в ту или иную сторону.
|
m |
n |
|
|
В случае если |
ai |
b j у некоторых поставщиков |
останется |
|
i |
1 |
j 1 |
|
|
|
|
|
m |
n |
неотправленная продукция, суммарный объем которой равен |
ai |
b j . |
||
|
|
i |
1 |
j 1 |
Чтобы привести задачу к закрытой задаче, вводится дополнительный столбец
так называемого «фиктивного» потребителя |
Bn 1 со спросом, равным избытку |
|||||
продукции. Все показатели ci, n 1 |
этого столбца полагаем равными нулю. |
|||||
|
m |
n |
|
|
|
|
В случае |
ai |
b j приведение к закрытой задаче достигается введением |
||||
i |
1 |
j 1 |
|
|
|
|
«фиктивного» |
поставщика Am 1 |
с |
объемом возможных поставок, равным |
|||
недостатку продукции |
|
|
|
|
||
|
|
|
n |
|
m |
|
|
|
|
|
|
b j |
ai . |
|
|
|
j |
1 |
i |
1 |
Стоимости перевозок сm+1, j , (j = 1, 2, …, n), от фиктивного поставщика ко всем потребителям принимаем также равными нулю.
Пример 2.
|
|
|
|
5 |
3 |
6 |
|
|
ai |
30,45,50,25 ; |
C |
cij |
5 |
1 |
6 |
. |
|
bj |
40,70,30 ; |
2 |
7 |
2 |
||||
|
|
|
||||||
|
|
|
|
8 |
3 |
7 |
|
Решение:
Проверим модель на сбалансированность:
4 |
|
|
|
|
|
|
|
3 |
|
|
|
|
ai |
a1 |
a2 |
a3 a4 |
30 |
45 |
50 |
25 150 , |
b j b1 b2 b3 |
40 |
70 |
30 |
140 . |
i 1 |
|
|
|
|
|
|
|
j 1 |
|
|
|
|
|
|
4 |
3 |
|
|
|
|
|
|
|
|
|
Так |
как |
ai |
b j , |
условие |
баланса |
не выполняется, |
данная |
модель |
||||
|
|
i 1 |
j |
1 |
|
|
|
|
|
|
|
|
является |
открытой. |
Приведём |
задачу к закрытому виду; |
введём |
фиктивного |
|||||||
86

4 |
3 |
|
потребителя B4 , потребность которого равна b4 |
ai |
b j 150 140 10 ед. |
i 1 |
j |
1 |
груза. Стоимости перевозки единицы груза (тарифы) для фиктивного потребителя принимаются равными 0.
Составим исходный план перевозок методом «наименьшего элемента» (минимальной стоимости). Поставки в клетки с нулевыми тарифами осуществляются в последнюю очередь.
1) Выбираем клетку (2,2) с наименьшим «реальным» тарифом равным 1. Записываем в эту клетку максимально возможную поставку 45 ед. груза, т.е. наименьшее из чисел a2 45 и b2 70 . Исключаем при этом из дальнейшего рассмотрения поставщика A2 (его возможности полностью исчерпаны). Запомним, что потребитель B2 еще нуждается в 70−45=25 ед. груза.
2) Минимальный тариф равный 2 соответствует двум клеткам (3,1) и (3,3) выбираем любую, например клетку (3,1), помещаем в эту клетку 40 ед. груза
( a3 |
50 , b1 |
40 ) и исключаем из рассмотрения потребителя B1 (его потребности |
|||||
полностью удовлетворены). У поставщика A3 |
ещё имеется в 50−40=10 ед. груза. |
||||||
3) |
Заполним клетку (3,3), которой соответствует минимальный тариф равный |
||||||
2, поставка в этой клетке равна 10 ( a3 |
10 , b3 |
30 ), исключаем из рассмотрения |
|||||
A3 . У потребителя B3 |
еще имеется потребность в 30−10=20 ед. груза. |
||||||
4) |
В оставшейся |
части таблицы |
наименьший тариф |
3 |
соответствует |
||
клеткам (1,2) и (4,2), |
выберем клетку (4,2) и поместим поставку |
25 ед. груза |
|||||
( a4 |
25,b2 |
25 ). Исключаем из рассмотрения два пункта A4 |
и B2 одновременно, |
||||
поэтому в клетку (4,3), стоящую рядом с клеткой (4,2) запишем 0. |
|
||||||
5)В клетку (1,3) помещаем 20 ед. груза ( a1 30,b3 20 ), исключаем потребителя B3 . При этом у поставщика A1 еще имеется в 30−20=10 ед. груза.
6)Заполним последнюю оставшуюся клетку (1,4) поставкой 10 единиц груза. Все запасы распределены, а потребности удовлетворены.
В опорном плане число занятых поставками клеток должно быть равно числу
m n 1 4 4 1 7 .
87
|
|
|
План- |
|
B1 |
|
B2 |
|
B3 |
|
|
B4 |
U i |
|
|
|
|
|
|
|
1 |
40 |
|
70 |
|
30 |
|
10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
30 |
|
5 |
|
3 |
|
6 |
|
|
0 |
U1 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
10 |
|
|
|
|
|
|
|
|
|
A1 |
-1 |
+ |
1 |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
5 |
|
1 |
|
6 |
|
|
0 |
U 2 |
3 |
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
0 |
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
50 |
|
2 |
|
7 |
|
2 |
|
|
0 |
U 3 |
0 |
|
|
|
|
|
|
|
40 − |
|
|
+ |
10 |
|
|
|
|
|
|
|
|
|
|
|
|
A3 |
|
|
9 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
25 |
|
8 |
|
3 |
|
7 |
|
|
0 |
U 4 |
5 |
|
|
|
|
|
|
|
|
|
25 |
0 |
|
|
|
|
|
|
|
|
||
|
|
|
A4 |
1 |
|
|
|
|
|
-1 |
|
|
|
|
|
|
|
|
|
|
V j |
V1 |
2 |
V2 |
2 |
V3 |
2 |
V4 |
4 |
Z1 |
340 |
|
|
|
|
Z1 |
6 |
20 |
0 10 |
1 45 |
2 |
40 |
2 10 |
3 |
25 |
7 |
0 |
120 |
45 |
80 |
20 |
75 |
340 . |
Проверим полученный план на оптимальность методом потенциалов: |
|
||||||
а) Потенциалами |
строк – |
U i |
и |
столбцов – V j |
называются |
числа, |
|
удовлетворяющие |
условию |
U i |
V j |
cij |
для базисных |
переменных |
(для |
заполненных клеток). |
|
|
|
|
|
|
|
Так как система для |
определения |
потенциалов |
содержит на |
одно |
|||
уравнение меньше, чем число потенциалов, то, чтобы найти решение системы потенциалов, один потенциал задаём произвольно, например, U3 0 .
Остальные потенциалы найдём, решая систему уравнений:
U1 |
V3 |
6, |
V1 |
2 U3 |
2 0 |
2, |
|
U1 |
V4 |
0, |
V3 |
2 |
U3 |
2 0 2, |
|
U 2 |
V2 |
1, |
U 4 |
7 V3 |
7 2 5, |
||
U3 |
V1 |
2, |
V2 |
3 |
U4 |
3 5 |
2, |
U3 |
V3 |
2, |
U 2 |
1 |
V2 |
1 |
2 3, |
U 4 |
V2 |
3, |
U1 |
6 |
V3 |
6 2 |
4, |
U 4 |
V3 |
7, |
V4 |
U1 |
4. |
|
|
б) |
Определяем характеристики для свободных клеток по формуле |
Eij cij |
U i V j и запишем их в левом нижнем углу свободных клеток. План |
является оптимальным если все Eij 0 .
88
E11 |
5 |
(4 |
2) |
1; |
E23 |
6 |
3 |
2 |
1; |
E34 |
0 |
0 |
4 |
4; |
E12 |
3 |
4 |
2 |
1; |
E24 |
0 |
3 |
4 |
1; |
E41 |
8 |
5 |
2 |
1; |
E21 |
5 |
3 |
2 |
0; |
E32 |
7 |
0 |
2 |
9; |
E44 |
0 |
(5 |
4) |
1. |
План 1 не оптимален, так как E11 0 и E44 0 .
Улучшим план. Выберем клетку с наименьшей отрицательной характеристикой, например, клетку (1,1) пометим знаком «+» и построим для неё контур:
(1,1) |
(1,3) (3,3) (3,1). |
Контур удовлетворяет |
следующим условиям: это замкнутая ломаная, |
состоящая из вертикальных и горизонтальных отрезков; отрезки контура могут пересекаться; все вершины контура находятся в заполненных клетках, за исключением той клетки, для которой он строится; число вершин ─ чётное.
Клетки, в которых находятся вершины контура, поочередно помечаем знаками «+» и «─». Из клеток, помеченных знаком «─», выбираем наименьшую
поставку |
min 20,40 20 . Число |
перераспределяется по контуру, в |
клетках со знаком «+» добавляется |
, в клетках со знаком «─» отнимается . |
|
После перераспределения груза, только одна вершина контура становится свободной.
Строим новый план перевозок.
План- |
|
B1 |
|
B2 |
|
B3 |
|
B4 |
U i |
|
2 |
40 |
|
70 |
|
30 |
|
10 |
|
|
|
30 |
|
5 |
|
3 |
|
6 |
|
0 |
U1 |
3 |
|
20 |
|
|
|
|
|
10 |
|
|
|
A1 |
+ |
|
2 |
|
1 |
|
− |
|
|
|
45 |
|
5 |
|
1 |
|
6 |
|
0 |
U 2 |
2 |
|
|
|
45 |
|
|
|
|
|
|
|
A2 |
1 |
|
|
|
2 |
|
1 |
|
|
|
50 |
─ 2 |
|
7 |
+ |
2 |
|
0 |
U 3 |
0 |
|
|
20 |
|
|
30 |
|
|
|
|
||
A3 |
|
|
9 |
|
|
|
3 |
|
|
|
25 |
|
8 |
|
3 |
─ 7 |
+ |
0 |
U4 |
5 |
|
|
|
|
25 |
|
|
0 |
|
|
|
|
A4 |
1 |
|
|
|
|
|
-2 |
|
|
|
V j |
V1 |
2 |
V2 |
2 |
V3 |
2 |
V4 |
3 |
Z2 |
320 |
Затраты на реализацию плана 2 составляют:
Z1 |
5 |
20 |
0 10 |
1 45 |
2 |
20 |
2 |
30 |
3 |
25 |
7 |
0 |
100 |
45 |
40 |
60 |
75 |
320 . |
|
|
|
|
|
|
|
|
|
|
89 |
|
|
|
|
|
|
|
|

Найдем потенциалы строк и столбцов, для чего составим систему уравнений. |
|||||||||||||||||
Потенциал |
U 3 |
примем равным 0. |
|
|
|
|
|
|
|
||||||||
|
U1 |
|
V3 |
5, |
V1 |
2 U3 |
2 0 2, |
|
|
|
|
|
|
||||
|
U1 |
|
V4 |
0, |
V3 |
2 U3 |
|
2 0 2, |
|
|
|
|
|
|
|||
|
U 2 |
|
V2 |
1, |
U4 |
7 V3 |
|
7 2 5, |
|
|
|
|
|
|
|||
|
U3 |
|
V1 |
2, |
V2 |
3 U4 |
|
3 5 |
2, |
|
|
|
|
|
|||
|
U3 |
|
V3 |
2, U2 |
1 V2 |
1 |
2 |
3, |
|
|
|
|
|
||||
|
U 4 |
|
V2 |
3, |
U1 |
5 V3 |
5 2 3, |
|
|
|
|
|
|
||||
|
U 4 |
|
V3 |
7, V4 |
0 U1 |
|
3. |
|
|
|
|
|
|
|
|||
Определим характеристики для свободных клеток. |
|
|
|
||||||||||||||
E12 |
3 |
3 |
2 |
2; |
E23 |
6 |
2 |
2 |
2; |
E34 |
0 |
0 |
3 |
3; |
|
||
E13 |
6 |
(3 |
2) |
1 |
E24 |
0 |
2 |
3 |
1; |
E41 |
8 |
5 |
2 |
1; |
|
||
E21 |
5 |
2 |
2 |
1; |
E32 |
7 |
0 |
2 |
9; |
E44 |
0 |
(5 |
3) |
2. |
|
||
План 2 не является оптимальным, т.к. E44 |
2 |
|
|
|
|
||||||||||||
После применения, рассмотренного выше алгоритма, получили план 3. |
|||||||||||||||||
|
|
|
|
План-3 |
|
B1 |
|
B2 |
|
B3 |
|
B4 |
U i |
||||
|
|
|
|
|
|
|
40 |
|
|
70 |
|
30 |
|
10 |
|
|
|
|
|
|
|
|
|
30 |
|
5 |
|
|
3 |
|
6 |
|
0 |
U1 |
3 |
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
|
A1 |
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
45 |
|
|
5 |
|
1 |
|
6 |
|
0 |
U2 |
1 |
|
|
|
|
|
|
|
|
|
|
45 |
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
2 |
|
|
|
|
3 |
|
2 |
|
|
|
|
|
|
|
|
|
|
50 |
|
|
2 |
|
7 |
|
2 |
|
0 |
U 3 |
0 |
|
|
|
|
|
|
|
20 |
|
|
|
30 |
|
|
|
|
|
|
|
|
|
|
A3 |
|
|
|
|
7 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
25 |
|
|
8 |
|
3 |
|
7 |
|
0 |
U4 |
3 |
|
|
|
|
|
|
|
|
|
|
25 |
|
|
|
0 |
|
|
|
|
|
|
|
A4 |
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
V j |
|
V1 |
2 |
V2 |
0 |
V3 |
2 |
V4 |
3 |
Z2 |
320 |
|
План 3 является оптимальным, т, к. все |
Eij |
0 . Затраты на реализацию |
|||||||||||||||
оптимального плана составляют Z3 |
320 . |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
90 |
|
|
|
|
|

ЗА Д А Ч И
1.Откорм животных выгоден тогда, когда каждое животное будет получать в дневном рационе не менее 6 единиц питательного вещества А, не менее 12 единиц вещества В и не менее 4 единиц вещества С. Для кормления используются два вида кормов. В таблице указано сколько единиц каждого питательного вещества содержит 1 кг каждого вида корма:
Питательные |
|
|
вещества |
Корм 1 |
Корм 2 |
|
|
|
А |
2 |
1 |
В |
2 |
4 |
С |
0 |
4 |
Цена 1-го корма – 5 руб. за 1 кг, 2-го – 7 руб. за 1 кг.
Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты на них были минимальными?
2. Для изготовления столов и шкафов употребляют два вида древесины. Расход древесины каждого вида на каждое изделие задан в таблице (в м3):
Изделие |
Древесина |
Доход с изделия |
|
|
1 вид |
2 вид |
(в тыс. руб.) |
Стол |
0,15 |
0,2 |
120 |
Шкаф |
0,3 |
0,1 |
150 |
Количество древесины |
60м3 |
40м3 |
|
Сколько столов и шкафов должна изготовить мастерская, чтобы обеспечить максимальный доход производства?
3. Для выпуска определённого вида продукции могут применяться два технологических способа с различным соотношением ручного и механизированного труда. Затраты ресурсов для производства единицы продукции, а также объём имеющихся ресурсов приведены в таблице:
91
Ресурс |
Объём ресурсов |
Технологический способ |
|
|
|
I |
II |
Труд (чел/ч ) |
|
|
|
Оборудование, |
240 |
5 |
8 |
(машино/ч) |
120 |
2 |
3 |
Цена ед. |
|
1 |
1 |
продукции |
|
|
|
Составить план производства продукции, обеспечивающий максимальный доход.
4. Предприятие может выпускать продукцию трёх видов – А, Б, В. Уровень выпуска лимитируется ограниченностью ресурсов – сырья, материалов и оборудования. Затраты на единицу изделия и объём ресурсов указаны в таблице:
Вид ресурсов |
Объём |
Норма затрат ресурсов на ед. продукции |
||
|
ресурсов |
А |
Б |
В |
Сырьё, кг |
240 |
5 |
7 |
4 |
Материалы, кг |
800 |
10 |
5 |
20 |
Оборудование 1 |
100 |
5 |
2 |
1 |
Оборудование 2 |
60 |
2 |
1 |
1 |
|
|
|
|
|
Прибыль от |
|
|
|
|
единицы |
|
18 |
12 |
8 |
продукции |
|
|
|
|
Определить объем выпуска продукции каждого вида, обеспечивающий максимальную прибыль, при условии, что продукции типа В должно быть выпущено не менее 20 изделий.
5. Консервный комбинат закупает яблоки у двух поставщиков . Для производства продукции ему необходимо 100 т яблок первого сорта, 60 т яблок второго сорта и 10 т – третьего сорта. Яблоки закупаются несортированные, но известно, что у первого поставщика 70 % яблок первого сорта и 30 % – второго, у второго поставщика 60 % яблок первого сорта, и 30 % – второго и 10 % – третьего. Затраты комбината на покупку и перевозку 1 т составляют 80 тыс. руб. для первого поставщика и 60 тыс. руб. для второго. Требуется осуществить закупку и перевозку яблок так, чтобы затраты были минимальными.
92
6. Со станции отправляются формируемые здесь пассажирские и скорые поезда. Они отличаются по количеству вагонов разных типов. Количество вагонов разных типов ограничено. Требуется найти такое соотношение количества пассажирских и скорых поездов, чтобы общее число мест в них было максимальными. Исходные данные по комплектации поездов даны в таблице:
|
|
|
Тип вагонов |
|
|
|
|
|
|
|
|
|
Багажные |
Почтовые |
Плацкартные |
Купейные |
Мягкие |
|
|
|
|
|
|
Кол-во вагонов в |
|
|
|
|
|
скором |
1 |
- |
5 |
6 |
3 |
Кол-во вагонов в |
|
|
|
|
|
пассажирском |
1 |
1 |
8 |
4 |
1 |
Кол-во мест |
|
|
|
|
|
в вагоне |
- |
- |
58 |
40 |
32 |
Кол-во |
|
|
|
|
|
вагонов на |
12 |
8 |
84 |
70 |
21 |
станции |
|
|
|
|
|
|
|
|
|
|
|
7. Грузовая автобаза, обслуживающая пять объектов строительства, развозит песок с трёх карьеров суммарной производительностью 700 т песка в сутки (соответственно 250, 300, 150 т). В таблице указанно расстояние от карьеров до потребителей (км):
Карьер |
|
Объект строительства (потребитель) |
|
|||
(поставщик) |
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
5 |
|
|
|
|
|
|
|
|
I |
11 |
7 |
20 |
9 |
|
15 |
|
|
|
|
|
|
|
II |
12 |
6 |
8 |
12 |
|
20 |
|
|
|
|
|
|
|
III |
18 |
15 |
20 |
16 |
|
19 |
|
|
|
|
|
|
|
Суточные потребности на объектах соответственно равны 140, 160, 100, 120, 180 т.
Составить план перевозок песка, обеспечивающий минимум объёма перевозок в тоннокилометрах.
8. Определить оптимальный план перевозок горючего из складов районного объединения “Сельхозтехники” на склады сельхозпредприятий. Исходные
93
данные о мощности и потребности горючего, а также расстояние между складами приведены в таблице:
Склады |
|
Склады сельхозпредприятий |
|
Мощность |
||||
“Сельхозтехники” |
|
|
|
|
|
|
|
складов |
В1 |
|
В2 |
|
В3 |
В4 |
В5 |
||
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
А1 |
|
20 |
|
64 |
45 |
34 |
18 |
2 000 |
А2 |
|
48 |
|
14 |
55 |
32 |
50 |
1 500 |
А3 |
|
15 |
|
10 |
25 |
39 |
40 |
1 600 |
Потребность |
|
700 |
|
850 |
1 000 |
1 800 |
600 |
|
колхоза в горючем |
|
|
|
|
|
|
|
|
9. Для пошива 120 комплектов изделий на швейной фабрике необходимо меть заготовки материала в 2,2 м; 1,8 м; 0,7 м. Каждый рулон материала содержит 20 метров. Найти такие способы раскроя материала, чтобы количество использованных рулонов было минимальным (при сохранении комплектности).
10. Необходимо изготовить 80 комплектов заготовок трёх видов длиной в 3 м; 2,4 м; и 1,8 м из стержней длиной 7,8 м. Найти способы раскроя и определить, какие из способов раскроя следует выбрать, чтобы число используемых стержней было минимальным.
11. 8. С двух заводов поставляются автомобили для двух автохозяйств, потребности которых соответственно 200 и 300 машин. Первый завод выпустил 350 машин, а второй – 150 машин. Минимальные затраты на перевозку равны 7 950 ден.ед. Известны затраты на перевозку машин с завода в каждое автохозяйство (см. таблицу).
Завод |
Затраты на перевозку в |
|
|
автохозяйства, ден. ед. |
|
|
I |
II |
1 |
15 |
20 |
2 |
8 |
25 |
Найти оптимальный план перевозок машин.
94
Библиографический список
1.Высшая математика для экономистов : учебник для студентов вузов, обучающихся по экономическим специальностям / под ред. проф. Н. Ш. Кремера. – М. : ЮНИТИ-ДАНА. 2007. – 479 с.
2.Высшая математика. Общий курс / под ред. А. И. Яблонского. – Минск : Высшая школа,1993.
3.Интриллигатор М. Математические методы оптимизации и экономическая теория. – М. : Прогресс, 1975.
4.Карасев А. К. Курс высшей математики для экономических вузов / Карасев А. К., Аксютина З.М., Савельева Т.Н. – М. : Высшая школа,
1982. – Ч. 1, 2.
5.Колемаев В. А. Математическая экономика : учебник для вузов / В. А. Колемаев. – М. : ЭНИТИ ДАНА, 2002. – 399 с.
6.Красс М. С. Основы математики и её приложения в экономическом образовании / М. С. Красс, Б. П. Чупрынов. – М. : Дело, 2011.
7. Математическая экономика : учеб. пособие / под ред.
В.А. Дыхта.  Иркутск : ИГЭА, 1996. – 32 с.
Иркутск : ИГЭА, 1996. – 32 с.
8.Мясников Е. А. Математика в экономике: примеры приложений : метод. указания / Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2013.
9.Мясников Е. А. Практикум по математическому анализу. Часть 1 : учеб. пособие / Е. А. Мясников. – Хабаровск : РИЦ ХГАЭП, 2012. – 100 с.
10.Практикум по высшей математике для экономистов : учеб. пособие для вузов / Н. Ш. Кремер [и др.]; под ред. проф. Н. Ш. Кремера. – М. :
ЮНИТИ-ДАНА, 2002. – 423 с.
11.Руководство к решению задач с экономическим содержанием по курсу высшей математики / под ред. А. И. Карасева и Н. Ш. Кремера. – М. : Экономическое образование, 1989.
12.Сборник задач по высшей математике для экономистов : учеб. пособие / под ред. В. И. Ермакова. – М. : ИНФРА-М, 2002. – 575 с.
13. Солодовников А. С. Математика в экономике : учебник / А. С. Солодовников [и др.]. – М. : Финансы и статистика, 1996. – 376 с.
14.Хайман Д. Н. Современная микроэкономика: анализ и применение. Т. 1, 2 / Д. Н. Хайман. – М. : Финансы и статистика, 1992.
15.Ясеновская И. В. Высшая математика. Приложения производной к исследованию функций : метод.  Хабаровск : РИЦ ХГАЭП, 2003.
Хабаровск : РИЦ ХГАЭП, 2003.
16.Ясеновская И. В. Статистические методы в экономических исследованиях с использованием Excel (Практикум) / И. В. Ясеновская. – Хабаровск : РИЦ ХГАЭП, 2007.
95
