Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5678.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

3.28 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

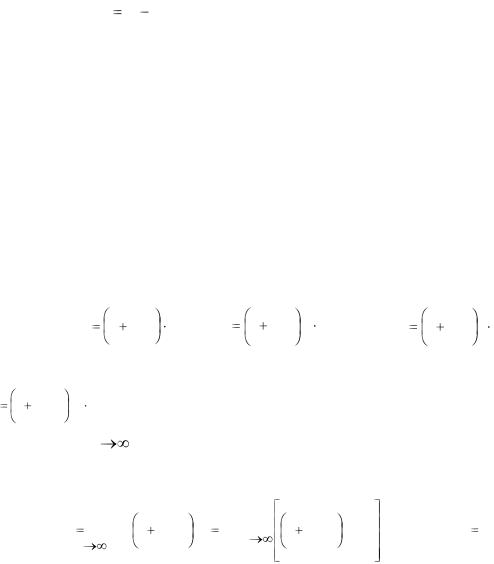
0 ≤ х ≤ 200 справедлива формула у = а / (х+с), причём при х =0, у = 150; при х = 200, у = 50. Вычислить, сколько минут выполняется работа при 50 операциях.

9. Рентабельность			у связана с себестоимостью продукции х следующей
зависимостью:	y	a	1, где а – цена единицы продукции. Построить график

		x

этой зависимости при а = 100. Пояснить его экономический смысл. Вычислить рентабельность при х1 = 50 и х2 = 150, дать пояснения.

3. ПОСЛЕДОВАТЕЛЬНОСТИ В ЭКОНОМИЧЕСКИХ ЗАДАЧАХ

3.1. Задачи о непрерывном начислении процентов

Предположим, что первоначальный вклад в банк составил Q0 денежных

единиц. Банк выплачивает ежегодно р% годовых. Необходимо найти

размер

вклада Qt через t лет.

Последовательно применяя формулу начисления процентов, получим

Q 1

, Q

, … , Qt

Q ,

100

если начислять

проценты

не

один

раз

в году,

а n

раз,

то

получим

Q 1

Q .

100n

Устремляя

, получим значение вклада через t лет при непрерывном

начислении процентов

100n 100

lim Q

lim 1

или

Q e100 .

100n

0 n

100n

Полученное уравнение называется рекуррентным уравнением динамики основного капитала.

В среднесрочных и долгосрочных моделях развития предприятия и экономики страны в целом обязательно участвует уравнение, описывающее динамику капитальных ресурсов, т.е. ресурсов, участвующих в процессе производства, изменение их во времени с учётом возможных инвестиций и износа. При этом предполагается, что ежегодные отчисления (амортизация)

составляют	постоянную	долю	(процент)	остаточной	стоимости
			17

амортизирующегося основного капитала. Эта доля называется коэффициентом

или нормой амортизации. Если норму				амортизации обозначить		через , а
величину основных		фондов	на начало	n-го года через Кn-1 (n=1, 2, …), то
получим	рекуррентное		уравнение	при	отсутствии	инвестиций
Кn=Кn-1 -	Кn-1 = (1-	) Кn-1 (n=1, 2, …).

Если же мы хотим учесть возможные инвестиции, то уравнение изменится. Пусть In – объём инвестиций n-го года. Тогда динамика капитала будет описываться рекуррентным уравнением

Кn = Кn-1 + In - Кn-1 = (1- ) Кn-1 + In (n=1, 2, …).

При этом начальное значение капитала К0 и объём инвестиций In считаются

известными. Предполагая, что существуют lim Кn	К	и lim In I и переходя в
n		n

этом уравнении к пределу при n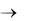, получим предельную стоимость основного капитала:

lim Кn	lim 1
n	n

или К =(1-

Кn 1 In	(1 ) lim Кn 1					lim In ,
			n			n
)К+I, т.е. К=		1	I	1	lim In .
)К+I, т.е. К=			I		lim In .
					n

Пример 1. Найти остаточную стоимость основного капитала на начало 3-го

года и			предельную								стоимость									основного капитала,												если				I	=	n2				2n		3		,
года и			предельную								стоимость									основного капитала,												если				I	=			2n2				1		,
																																								2n2				1
= 0,2,			К0=1 млн у.е.
Решение. Найдём										I1=		12		2	3			2		;
Решение. Найдём										I1=			2 12		1			3		;
													2 12		1			3
			К1 = (1-				)К0+I1 = (1-0,2)1+												2			4		2			22	;		I2 =	22			2	2		3		3		;
			К1 = (1-				)К0+I1 = (1-0,2)1+												3			5	3				15	;		I2 =	2			22	1			9			;
																			3			5	3				15				2			22	1			9
									К2= (1-					)К1 + I2					=		4		22			1		88		25		103	.
									К2= (1-					)К1 + I2					=				15			3		75				75	.
																			5				15			3		75				75
Предельную стоимость основного капитала найдём по формуле
К =	1	lim	I n	1		lim			n2		2n			3	5	1			2,5.
К =		lim	I n			lim					2				5				2,5.
		n			0,2 n				2n			1				2
Найдём				объём				инвестиций							в		первый								год		I1=		12	2 1 3					2		и	стоимость
Найдём				объём				инвестиций							в		первый								год		I1=			2 12	1				3		и	стоимость
																														2 12	1				3
основного капитала К1										на начало второго года К1=(1-																				)К0+I1=(1-0,2) 1+										2			22		.
основного капитала К1										на начало второго года К1=(1-																				)К0+I1=(1-0,2) 1+															.
																																						3				15

Затем найдём I2=	22	2	2	3		1	и стоимость основного капитала на начало
Затем найдём I2=	2	22	1		3		и стоимость основного капитала на начало
	2	22	1		3
третьего года К2= (1- ) К1 + I2				= (1-0,2)				22		1		103	.
третьего года К2= (1- ) К1 + I2				= (1-0,2)				15	3		75		.
								15	3		75

3.2. Паутинообразная модель рынка

Рассмотрим простейшую динамическую модель рынка некоторого товара. В этой модели предполагается, что объём спроса в любой текущий момент времени n t зависит от уровня цены этого периода – Рn, а предложение реагирует на изменение цены с некоторым запаздыванием и зависит от уровня цены в предыдущем периоде – Рn-1. Обозначим через QD(n) и QS(n) объёмы спроса и предложения в период n, тогда QD(n)=f(Pn) и QS(n)=g(Pn-1). Следующее предположение модели состоит в том, что изменение цены во времени происходит таким образом, что текущий спрос равняется текущему предложению, т.е. QD(n)=QS(n) или f(Pn)=g(Pn-1).

Чтобы упростить анализ этого уравнения, предположим, что f(Pn)=an-bPn, g(Pn-1)=Cn-1+dPn-1 (b>0, d>0). Подставив эти выражения в уравнение f(Pn)=g(Pn-1), получим уравнение аn-bPn=Cn-1+dPn-1, которые вместе с

равенствами QD(n)= аn-bPn, QS(n)= Cn-1+dPn-1 образует		так называемую
паутинообразную модель рынка.
Предположим, что существуют lim an	a, lim Cn C и	lim Pn P , тогда,
n	n	n

переходя

lim (an bPn )

в последнем	уравнении к пределу при n	, получим
lim (Cn 1 dPn	1) или a - bP = C + dP. Отсюда найдём
n

Р =	a	c	lim an	lim cn	.
Р =	d	b	d	b	.
			n	n

Можно показать,

что если

1 и существуют

lim a ,

lim c , то существует и

lim Pn

этом случае

называется

предельным значением

равновесных цен Рn.

Пример 2. Найти предельное значение равновесных цен в паутинообразной

модели рынка, если

, b 1,5,

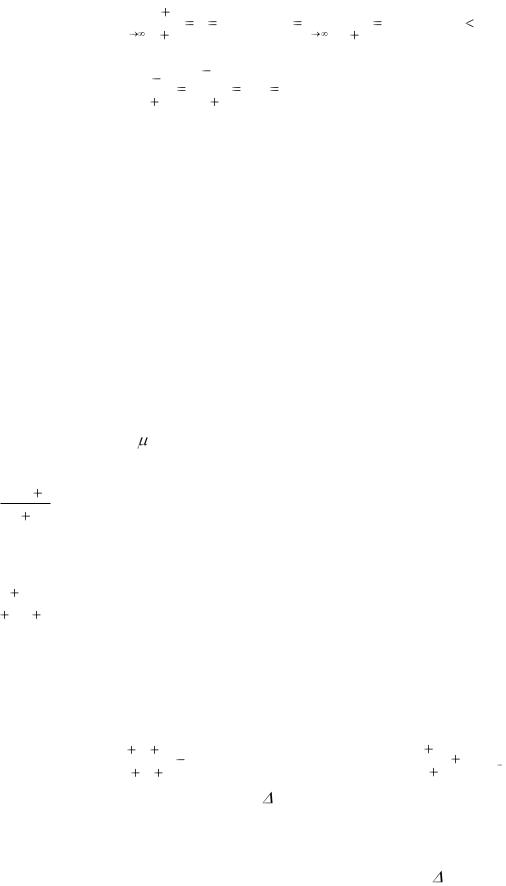
Решение.

Найдем

lim

и c lim

, т.к.

1 и а, с

2n 1

0,5

определены,

то Р =

0,2,

Р –

предельное

значение

1,5

2,5

равновесных цен

ЗА Д А Ч И

1.Годовая процентная ставка р = 9 %. Рассчитать величину вклада через пять лет, если начальный вклад Q0 = 2 000 руб., а проценты начисляются ежеквартально. Вычислить величину вклада через пять лет при непрерывном начислении процентов.

2.За два года величина вклада выросла в 1,4641 раза при начислении процентов раз в полгода. Во сколько раз возросла бы величина вклада при непрерывном начислении процентов?

3. Норма амортизации равна 10%. Найти остаточную стоимость основного капитала на начало 3-го года и его предельную стоимость, если инвестиции в n-й

год In = 0,2n 1 у.е. и начальное значение К0 = 2 у.е. n 3

4. Ежегодные инвестиции в основной капитал определяются равенством

In=	n	1		у.е. Определить предельную стоимость и начальную стоимость

	0,1n2	2n	1,9
	0,1n2	2n	1,9

основного капитала, если норма амортизации 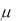= 5% и величина основного капитала на начало второго года К1 = 2,4 у.е.

5. Пусть спрос на некоторый товар в момент времени n определяется

равенством QD(n) =	n2	n	1	0,4Pn , а предложение QS(n)=	n	2	0,2Pn 1	, где
	2n2	n	1		3n	1

Рn – равновесная цена в момент времени n t. Определить значение равновесной цены Р3 и предельное значение равновесных цен Р, если начальная цена Р0=0,5.

6. Пусть Рn – значение равновесной цены в момент времени n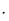 t. Определить Р3 и предельное значение равновесных цен Р, если начальная цена Р0=1, а

объёмы спроса				QD(n)	и предложения QS(n) определяются равенствами
Q (n)=	2n2	n	2	1,2 P ;	Q	(n)=	n2	n	1	0,8P	.

D	n2	n	1	n	S		n2	n	2	n 1

4. ПРОИЗВОДНАЯ. ПРЕДЕЛЬНЫЙ АНАЛИЗ

4.1. Экономический смысл производной

Пусть функция y = f(x) определена на промежутке X. Возьмём точку х X . Дадим значению х приращение х 0 , тогда функция получит приращение

у=f(x+ х)-f(x).

Производной функции y=f(x) называется предел отношения приращения

функции к приращению аргумента при стремлении последнего к нулю								(если
этот предел		существует):
		y		f ( x	x) f ( x)
y	lim		lim			.
y	lim		lim			.
	x 0	x	x 0		x
	Производная		функции	y x	характеризует мгновенный прирост			или
скорость изменения зависимой					переменной y (функции f(x))		в точке x.
	Пример 1.		Стоимость	определённой продукции на 1			рубль основных

производственных фондов (фондоотдача) y зависит от коэффициента сменности оборудования х (характеризующего степень равномерности использования

оборудования по сменам) следующим образом: y=

x +c, где

c –

постоянная

величина. Найти:

а)

скорость изменения

фондоотдачи

при

коэффициенте

сменности

оборудования x=1,35;

б) найти функцию этого изменения, если

c =

0, полагая, что некоторое

время фондоотдача будет меняться с постоянной скоростью.

Решение:

а)

скорость

изменения

фондоотдачи определяется производной y

при

x=1,35 ,

y=(1,35) =

0,43, т.е. при

изменении

коэффициента

2 1,35

сменности на единицу фондоотдача увеличивается приближенно на 0,43 руб.;

б) фондоотдача y будет меняться с постоянной скоростью v= y (1,35) = 0,43 в случае линейной зависимости, т.е. по касательной к кривой в точке x0=1,35; уравнение касательной имеет вид: y – 1,16 = 0,43 (x-1,35), где y(1,35)=1,16. После преобразования имеем уравнение фондоотдачи y=0,43x+0,58.

Пусть функция u = u (t) выражает количество произведённой продукции u за

время t . Необходимо найти производительность труда				в момент t0. За период
времени от t0	до	t0+	t количество произведённой	продукции изменяется
на величину	u	u(t 0 +	t) u(t 0). Тогда средняя производительность труда за

время

будет равна отношению

ср=

. Определим производительность

труда

момент

времени

как

предельное

значение

средней

производительности

при

t 0

, т.е.

lim

t 0

Таким

образом,

производительность

труда

есть

производная

объёма

произведённой продукции по времени.

Темпом изменения функции называется величина

Т y =

y (x)

(ln y) .

Пример 2. Производительность труда бригады рабочих может быть описана уравнением y = -2,5t2 + 15t + 100, 1 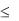t 8 – рабочее время в часах. Вычислить скорость и темп изменения производительности труда при t = 2, t = 7.

Решение. Скорость изменения производительности труда выражается производной

y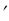= -5t + 15 y (2) = 5 ед/ч y (7) = -20 ед/ч.

Темп изменения (относительная скорость изменения) производительности

труда выражается формулой T =	y	5t 15		.
труда выражается формулой T =				.
y	y	2,5t 15 t	100
	y	2,5t 15 t	100

Тогда Ty (t =2) = 1/24 (ед/ч) , Ty(t=7) = -8/33(ед/ч) .

Знаки плюс и минус показывают, что в начале смены наблюдалось увеличение производительности, а в конце – снижение.

Рассмотрим ещё одно понятие, иллюстрирующее экономический смысл

производной. Пусть		К=К(х) функция издержек производства, где			х – объём
выпускаемой	продукции,		пусть	x – прирост продукции,	ему	будет
соответствовать	y	y(x x)	y(x)	приращение издержек производства.
				22

Величина	y	есть среднее приращение		производства		на единицу

	x
	x
продукции. Найдём предельные издержки lim			y	K (x).	К x	характеризует

			x
		x o	x
		x o

приближенно дополнительные затраты на производство дополнительной единицы продукции.

Предельные издержки зависят от уровня производства (количества

выпускаемой продукции)	х	и	определяются	не	постоянными
производственными затратами, а		лишь	переменными	(на сырьё, топливо,

электроэнергию, и т.п.). Аналогично могут быть определены предельная выручка, предельный доход, предельный продукт, предельная полезность и другие предельные величины.

Предельные величины характеризуют не состояние (как суммарная или средняя величина), а процесс изменения экономического объекта. Таким образом, производная выступает как скорость изменения некоторого экономического процесса по времени или относительно другого исследуемого фактора.

Пример 3. Пусть К(х)=50х-0,05х3

(ден.ед.) функция издержек производства.

Определить

средние и

предельные

издержки, если

объём составляет 10

условных единиц.

Решение.

Средние издержки

К х 50 x

0,05 x3

0,05 x2 , при х=10

К 10

=45 (ден.ед.).

Предельные издержки

К х =50 - 0,15х2

при х=10 К х =50 - 0,15 · 102 = 35 (ден. ед.).

Итак, если

средние

издержки

на

производство

единицы продукции

составляют

45 ден. ед.,

то предельные издержки, т.е. дополнительные затраты

на производство дополнительной единицы продукции при данном уровне производства (объёме выпускаемой продукции 10 ед.), составляют 35 ден.ед.

4.2. Эластичность функции. Свойства эластичности

Для исследования экономических процессов и решения других прикладных задач часто используется понятие эластичности функции. Эластичностью функции EX (у) называется предел отношения относительного

приращения функции у к относительному приращению аргумента х при

x	0
	Ех (y) = lim (	y	:	x	)	x	lim	y	x	y .
	Ех (y) = lim (	y	:		)	y	lim	x	y	y .
	x 0	y		x		y	x 0	x	y

Эластичность функции показывает приближенно, на сколько процентов

изменится функция	у= f(x)	при	изменении		независимой переменной х на
1%. Эластичность функции обладает рядом свойств:
1. Эластичность	функции	равна	произведению независимой переменной
х на темп изменения функции Ту =			(ln y)	y	, т.е.

				y
				y

Ех (у) = х ∙ Ту.

Эластичность произведения (частного) двух

функций

равна

сумме

(разности) эластичностей этих функций

Ex (u

v) = Ex (u) + Ex (v);

= Ex (u) – Ex (v)

Если

Ex ( y)

>1, то изменению

переменной

на 1%

соответствует

изменение функции более

чем

на 1%,

то

говорят,

что функция

эластична

относительно х.

Если

Ex ( y)

1, то

функция

нейтральна, т.е. изменение

на

приводит к изменению y(х) на 1%.

Если

Ex ( y)

<1, функция неэластична, при изменении х

на 1% функция

у(х) изменяется менее чем на 1%.

Пример 4. Пусть функция спроса

на

некоторый

вид товара

имеет

вид

q 2e 2 p , где p–цена товара

(ден.ед.). Определить эластичность спроса при цене

товара p=3 (ден.ед.).

Решение. Рассчитаем эластичность спроса относительно цены.

(q)

(2e 2 p )

2 p .

2e 2 p

Тогда Ep 3 (q) 2 3 6. Это означает, что при цене 3 (ден.ед.) повышение цены на 1% вызовет снижение спроса на 6%, т.е. спрос эластичен.

Пример 5. Пусть спрос на данный товар в зависимости от дохода потребителей выражается формулой q = r , где r – доход. Определить эластичность спроса относительно дохода.

Решение. Эластичность спроса относительно дохода имеет вид:

Er (q) =

0,5.

2 r

Это означает, что повышение дохода потребителей на 1% вызовет повышение спроса на товар на 0,5%.

p2 )

Пример 6.

Пусть S(p) =

–

функция предложения (товара, труда,

8 p

услуг)

в зависимости от цены р.

Найти

эластичность предложения при цене

товара р = 4 (ден. ед.).

Решение. Эластичность предложения относительно цены Ep (s)=

Ep (s) =

p (1

8 p)

p2 )

2 p ( p

4 p2 16)

3 (4 p2 )

1 8 p

(4 p2 ) (1 8 p)

При

р=4

эластичность

Ер(s)

0,7,

т.е. прирост предложения,

соответствующий увеличению цены р = 4 (ден.ед.) на 1%, составляет 0,7%.

4.3. Экстремум

функции

Пусть на промежутке Х задана функция у=f(x).

Необходимое

условие

экстремума.

Если

функция

у=f(x)

дифференцируема в

точке

х0

имеет

экстремум в этой точке, то

у ( х0 )

0 .

Первое достаточное условие экстремума. Если при переходе через точку

х0 производная дифференцируемой функции у=f(x) меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции у=f(x), а если с минуса на плюс, то х0 – точка минимума.

Второе достаточное условие экстремума. Если производная f (x)

дважды дифференцируемой функции равна нулю в некоторой точке x0									X , а
вторая производная			f (x0 )	положительна,		то х0	есть точка	минимума
функции f (x) , если			f (x0 ) отрицательна, то х0			точка максимума.
Пример	7.	Производитель			реализует	свою	продукцию по		цене
р=150 (ден.	ед)	за единицу,		а	издержки при этом		задаются	кубической
					25

зависимостью		S(x)=6x+3x3. Найти оптимальный объём выпуска продукции
при котором прибыль будет максимальной.
Решение.		Пусть	объём	выпускаемой продукции	х. Составим функцию
прибыли C(x) = 150x-(6x+3x3), где рх – доход от реализуемой продукции.
1.	Найдём	производную		C (x) 150 (6 9x2 ) 144	9x2 .
2.	Найдём критические точки.
C (x) 144		9x2 0		х1 = 4, х2 = – 4 (не удовлетворяет смыслу задачи).
3.	Найдём	C (x)	18x и определим знак второй производной при х=4

C(4) 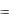72 0 , следовательно, при х=4 прибыль С(х) максимальна.

4.Находим максимум функции Сmax(x=4)=150 4 (6 4 364) 384 (ден.ед.). Пример 8. Капитал в 1 млрд руб. может быть размещён в банке под 50%

годовых или инвестирован в производство, причём эффективность вложения

ожидается

размере

100%, а издержки задаются квадратичной

зависимостью.

Прибыль облагается налогом в р%. При каких

значениях р

вложение в производство

является более эффективным, нежели чистое

размещение капитала в банке?

Решение.

Пусть

(млрд

руб.)

инвестируется

производство, а

(1-х) ‒ размещается

под

проценты.

Тогда

размещенный

капитал

станет

равным (1

x)(1

)

x ,

капитал,

вложенный

производство,

100

x(1

100

)

2x .

100

Издержки

составят

a х2,

т.е.

прибыль

от вложения в

производство

С = 2х - a х2.

Налоги

составят

(2х -

a х2)

т.е.

чистая

прибыль

окажется

100

равной (1

)(2x

ax2 ) .

100

Общая сумма через год составит:

A(x)

)(2x

ax2 )

2(1

)

a(1

)x2 .

100

Требуется найти максимальное								значение						этой			функции на отрезке									0;1 .
Для этого найдём производную функции													A (x)			2(1			p	)		3	2a(1		p	)x и
Для этого найдём производную функции													A (x)			2(1			100	)	2		2a(1	100		)x и
																			100		2			100
									2(1					p	)		3
приравняем её к нулю A (x)						0 , при		x	2(1				100		)	2		.
													100			2

								0							p
											2a(1				p	)
											2a(1					)
													100
Вторая производная					A (x)		2a(1			p		)	0 ,				т.е.,				согласно			второму
Вторая производная					A (x)		2a(1					)	0 ,				т.е.,				согласно			второму
									100
достаточному условию экстремума,								х0 – точка максимума.
Чтобы точка		х0		принадлежала отрезку [0;1],														необходимо					выполнение
условия 0< 2 (1-		p	)	3	1	или	р < 25.
условия 0< 2 (1-			)		1	или	р < 25.
	100			2

Таким образом, если р > 25, то выгоднее ничего не вкладывать в

производство и разместить весь капитал в							банк. Если р < 25 , то можно
показать, что при х = хо
			2 1		p		3	2
	3
A(x0 ) =		+		100			2	3	A(0).
				100			2	3
	2
			4a 1			p		2
						p		2

					100
					100

Таким образом, вложение в производство является более выгодным, чем чистое размещение под проценты.

4.4. Определение оптимального размера партии

Для определения оптимального размера партии изделий введём обозначения:

пусть С1 – затраты на хранение одного изделия в единицу времени;		С2 – общие
затраты на производство одной партии;	n – число изделий	в партии;
Т – продолжительность производства одной партии.
Требуется определить размер партии n,	при котором обработка N изделий

(N>n) за время t потребует минимальных затрат.

Составим		функцию у=f(х), выражающую зависимость суммарных затрат у
от размера партии n.
Общее	число партий		N	,	тогда общие затраты на производство

			n
составят C2	N	. При определении затрат на хранение будем исходить из того,
	n

что партия изделий по мере изготовления поступает на хранение и поэтому за период её изготовления Т хранится в среднем n2 изделий.

Таким

образом, затраты

на хранение

одной партии

составляют

С1

T .

C1TN

Суммарные

затраты

на

хранение

составят

Суммарные

затраты

на

производство

хранение

будут

составлять

y C

TN .

Величины

n и T

взаимозависимые, очевидно, что

NT nt .

Подставляя в функцию y, получим y

C2 N

C1t

n .

Исследуем функцию у = f(n) на минимум (С1, С2, N и t – заданные величины).

Вычислим производную функции y

C2 N

C1t

приравняем её к нулю

n 2

y 0 ,

C2 N

C1t

0 ,

n 2

Вычисли вторую производную функции

2C2 N

, при найденном n0

функция достигает минимума.

Итак, оптимальный размер партии, минимизирующий суммарные затраты

равен	n	2NC2	.

	0	t C1

Пример 9. Пусть планируется строительство и эксплуатация некоторого объекта, срок эксплуатации Т лет. Первоначальные капиталовложения составляют К руб., а последующее ежегодные эксплуатационные расходы х руб. Предположим, что первоначальные капиталовложения зависят от последующих ежегодных расходов К=f(х). Определить оптимальный размер первоначальных капиталовложений, при котором суммарные расходы достигают минимума.

Решение

Суммарные расходы по строительству и эксплуатации данного объекта за Т лет составят y K x T f (x) xT.

Исследуем функцию на минимум

	y	K	T	f x	T ,
y	0 ,	K	T	0 , K	T .
Из уравнения следует, что K < 0, т.е. начальные вложения убывают с ростом
ежегодных эксплуатационных расходов.
Если K >0, то кривая	К=f(х)		вогнутая,		т.е. если с ростом годовых

эксплуатационных расходов, уменьшение начальных капиталовложений

происходит с замедлением, то найденное значение х* из уравнения K	T ,
определяет минимальные суммарные затраты ymin = f(x ) + x ∙ T.

4.5. Функция двух переменных

Пусть имеются две переменных х и у, и каждому набору их значений (х, у) из некоторого множества U соответствует одно вполне определенное значение

переменной величины

Z. Тогда говорят,

что задана функция двух переменных

Z=f(x, у).

Дадим

аргументу х приращение

х, аргументу у – приращение

у.

Величина

f (x

x, y

f (x, y) называется полным приращением

функции в точке (х,у).

Если задать только

приращение

аргумента

или аргумента

у,

то

полученные приращения

функции соответственно

x Z=f(x+

x,y)-f(x,y)

y Z= f(x,y+

y)-f(x,y) называются частными.

Частной производной

функции

z=f(x,y)

по

независимой

переменной

называется функция переменных

х и у,

полученная

при дифференцировании

f(x,

по

предложении,

что

считается

постоянной

(x, y)

lim

x z

x 0

Аналогично частной производной по у

будет Z

f y (x, y)

lim

y z

y 0

Частная производная по переменной х в точке (х,у) характеризует скорость изменения или прирост переменной Z при изменении х и постоянном значении

у.

Коэффициентами частной эластичности Ex(z), Ey(z) называются величины

Ex (z)	x	Zx ,	Ey (z)	y	Z y .
Ex (z)	z	Zx ,	Ey (z)	z	Z y .
	z			z
					29

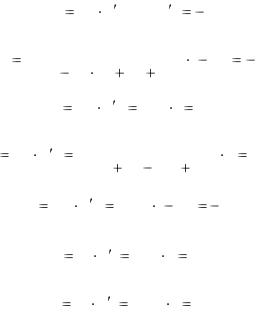
Коэффициент частной эластичности Ex(z) приблизительно показывает, на сколько процентов изменится функция при изменении переменной x на 1% при неизменном значении у.


Пример 10.	Функции спроса на товары А и В имеют вид:
х = 1000 - 20 р1 + р2 + 2m ;		у = 2000 + 2р1 – 10р2 + 3m,
где x, p1	и y, p2 – спрос на товары А и В и их цены соответственно, m –

часть дохода потребителя, которую он расходует на приобретение названных товаров. Определить коэффициенты эластичности функций при p1 = 40, p2 = 50, m = 100.

Решение

				E x p							p1	x p								x p			20.
				E x p							x	x p								x p			20.
							1				x				1						1
							1								1						1
E xp												40										(	20)		1,8.

		1000							20			40				50		200
	1	1000							20			40				50		200
			E x								p2	x						50			1	0,11.
			E x			p	2				x	x	p		2	450					1	0,11.
							2				x				2	450
E y p			p1		y p											40								2	0,043 .
E y p			y		y p				2000							80		500				300		2	0,043 .
1			y				1		2000							80		500				300
1							1
	E y p						p2				y p					50			(		10)		0,27.
	E y p				2			y			y p	2		1880					(		10)		0,27.
					2			y				2		1880
					E xm						m	xm					100				2	0,44.
					E xm						x	xm				450					2	0,44.
											x					450
				E ym						m		уm					100				3	0,16.
				E ym							у	уm				1880					3	0,16.
											у					1880
Величины Exp1 = -1,8		и Eyp1=0,043 показывают, что с ростом цены товара А

на 1%, спрос на товар А снижается на 1,8%, а спрос на товар В повышается на

0,043%.

Аналогично величины Еxр2 и Еyр2 показывают, что с увеличением цены товара В на 1%, спрос на товар А повышается на 0,11%, а спрос на товар В снижается 0,27%.

4.6. Экстремум функции двух переменных

Пусть на множестве U задана функция Z=f(x,y).

Необходимое условие экстремума функции двух переменных – равенство частных производных нулю.

	zx fx (x, y)	0 ; z	y	f	y	(x, y) 0.
			y		y
Достаточное условие экстремума функции двух переменных.
Пусть (х0,у0) – критическая точка функции Z=f(x,y)							, т.е. fx (x0 , y0 ) 0	и
f y (x0 y0 )	0 , а значение вторых частных производных						функции z=f(x,y)	есть
fxx (x0 y0 )	A, fx, y (x0 y0 ) B , f yy (x0 y0 )	C .

Тогда

–если = АС– В2 >0, то функция Z=f(x,y) в точке (х0 у0) имеет экстремум: максимум при А<0;

минимум при A>0;

–если = АС– В2 <0, то экстремума нет;

–если = АС– В2 =0, то вопрос о наличии экстремума остаётся открытым. Пример 11. Фирма продаёт товар на двух рынках в количествах x и y. Заданы

функции дохода фирмы на каждом из этих рынков:

R1(х) = (351 – х) 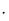х , R2(у) = (451 – 2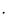у) у.

Функция полных издержек фирмы имеет вид C = Q2 + Q + 10, где Q = х + у. Определить, при каком объёме выпуска продукции достигается максимум

прибыли и какая часть продукции должна продаваться на втором рынке.

Решение

Поскольку прибыль равна разности между доходом от продаж и полными издержками производства J = (351 – х)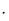х + (451 – 2у) у ‒ C =

= 351 х – х2 + 451 у – 2у2 – (х+у)2 ‒ х ‒ у‒ 10 = 350 х + 450 у ‒ 2x2 ‒ 3у2 – 2ху ‒ 10

Необходимое условие экстремума дифференцируемой функции – равенство

частных производных J x и J y нулю.
J x	= 350 ‒ 4х		‒	2у;
J y	= 450 ‒	6у	‒	2х.
Получим систему линейных уравнений:
	4x 2 y	350		0
	2x 6y 450 0 .
Решив систему уравнений, получим x= 60,			y = 55.
Проверим достаточное условие экстремума:
A = J xx = - 4;
B = J xy = - 2;
	31

<<< < Предыдущая 1 23 / 63 4 5 6 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20223.06 Mб25673.pdf
#
13.11.20223.06 Mб35674.pdf
#
13.11.20223.08 Mб25675.pdf
#
13.11.20223.08 Mб35676.pdf
#
13.11.20223.24 Mб15677.pdf
#
13.11.20223.28 Mб35678.pdf
#
13.11.20223.35 Mб35679.pdf
#
13.11.20223.35 Mб25680.pdf
#
13.11.20223.39 Mб75681.pdf
#
13.11.20223.39 Mб55682.pdf
#
13.11.20223.4 Mб85683.pdf