C = J yy = - 6;

= АС– В2 = 24 – 4 = 20 > 0; A<0.

В точке x= 60 y = 55 имеет место максимум функции прибыли.

Таким образом, оптимальный объём выпуска продукции Q = 135, причём на втором рынке должен продаваться (55/135)·100=41% от общего объёма производства.

4.7. Метод наименьших квадратов

Пусть между переменными величинами х и у имеется или предполагается некоторая функциональная зависимость y=f(x), подлежащая определению. С этой целью выполнены наблюдения, а результаты их представлены в таблице в виде n пар соответствующих значений переменных x и у:

Эти данные можно представить графически, если в прямоугольной системе координат построить точки, координаты которых – пары соответствующих значений переменных х и у , т.е. точки А1(х1,у1), А2(х2,у2), …, Аn(xn,yn).

Предположим что анализ опытных данных (в том числе и расположение точек А1, А2,…,Аn на плоскости) привёл к выводу, что между переменными х и у существует линейная зависимость которая графически изображается прямой на плоскости

ординат точек A1, A2,…An и ординат точек на прямой (4.1), имеющие одинаковые с точками A1, A2,…An абсциссы минимальна. Параметры a и b этой «наилучшей» прямой определяются из системы уравнений:

Система (4.2) называется системой нормальных уравнений.

32

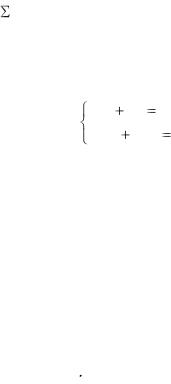
Пример 12. Данные о стоимости основных производственных фондов пяти предприятий х (млн руб.) и среднесуточной переработки свёклы у (тыс.ц) приведены в таблице:

Предполагая, что между переменными х и у существует линейная зависимость, необходимо: а) найти параметры этой зависимости, используя метод наименьших квадратов; б) определить среднесуточную переработку свёклы предприятием, имеющим стоимость основных фондов 9 млн руб.

Решение. Результаты вспомогательных вычислений для получения коэффициентов системы нормальных уравнений (4.2) поместим в следующей таблице:

Следовательно, система нормальных уравнений при n = 5 ( число пар значений переменных) имеет вид

25a 5b 38,

135a 25b 206.

Решим систему и найдем а= 1,6, b = – 0,4, а искомая функциональная зависимость такова: у = 1,6x –0,4.

Среднесуточную переработку свёклы предприятием, имеющим стоимость основных фондов 9 млн руб. найдём, подставив значение x=9 в найденное уравнение зависимости между х и у:

ух=9 = 1,6 9 – 0,4 = 14 (тыс.ц).

Предположим, что зависимость между переменными х и у выражается показательной функцией

Логарифмируя обе части этого уравнения, получим lgy = x ∙ lga + lgb.

33

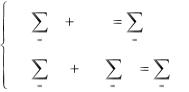
Следовательно, между значениями переменной x и логарифмами значений переменной у существует линейная зависимость с параметрами lga и lgb. Поэтому, если воспользоваться способом наименьших квадратов, то логарифмы а и b параметров функции (4.3) определяются из системы уравнений

Предполагая, что рост численности персонала происходил по показательной кривой у = bаx, найти параметры a и b этой зависимости, пользуясь способом наименьших квадратов.

Решение. Систему координат выберем так, чтобы её начало соответствовало 2005 г. – это упростит вычисления. Следовательно, при решении задачи исходим из следующих данных:

Следовательно, искомая функциональная зависимость такова:

у = 19 124 1,129 х .

Уравнение показывает, что численность персонала в среднем росла ежегодно

в1,129 раза, или на 12,9% ежегодно.

Вслучае если между переменными х и у существует гиперболическая зависимость

значениями переменной у существует линейная зависимость. Поэтому, если воспользоваться способом наименьших квадратов, то параметры а и b функции (4.5) определяются из следующей системы нормальных уравнений:

Предполагая, что между переменными х и у существует гиперболическая зависимость y= ax b , найти параметры a и b этой зависимости, пользуясь способом наименьших квадратов.

35

Решение. Результаты вспомогательных вычислений поместим в таблице:

Подставляя полученные значения в систему (4.6) при n = 6 (число пар соответствующих значений переменных х и у), получим

18782a 6b 134,

1,1921a 1,8782b 53,3148 .

Решая систему, найдём а = 18,8166 18,8 b = 16,4421 16,4.

Следовательно, искомая функциональная зависимость имеет вид:

то параметры а0, а1, а2 функции (4.7) определяются из следующей системы нормальных уравнений:

Пример 15. Ниже приведены данные о помесячной выработке мяса:

мяса, кг

Установить вид функциональной зависимости в изменении выработки мяса и найти параметры этой зависимости с помощью метода наименьших квадратов.

Решение. Данные таблицы показывают, что выработка мяса в начале года убывает, а затем возрастает. Это даёт основание полагать, что искомой функциональной зависимостью является параболическая (4.7).

Для упрощения вычислений за начало отсчёта времени возьмём середину ряда, т.е. будем считать, что месяцам года соответствуют следующие условные числа:

Подставляя найденные численные значения в систему (4.8), получим

Итак, искомая зависимость имеет вид у = 20 998 + 2 951х + 354х2 .

37

Рекомендуем читателю построить в прямоугольной системе координат данные условия примеров 12 – 15 (точки, координаты которых – пары соответствующих значений переменных) и графики найденных функций (на одном чертеже для каждого примера) и убедиться в том, что соответствующие прямая и кривая (показательная кривая, гипербола, парабола) хорошо воспроизводят расположение точек, построенных на основании этих примеров.

предельные издержки при объёмах х = 10, х=20, х=30 условных единиц продукции.

2. Себестоимость продукции y связана с объёмом продукции х уравнением y = 6ln(1+3x). Определить среднюю и предельную себестоимость продукции при объёме 10 ед.

3.Задана функция полных затрат в виде y = x3 – 2x2. При каком объёме производства х предельные и средние затраты совпадают?

4.Зависимость между объёмом выпуска готовой продукции однотипных предприятий y (млн руб.) и объёмом производственных фондов х (млн руб.) выражается уравнением y = 0,6 х – 4. Найти коэффициент эластичности выпуска продукции для предприятий, имеющих фонды 40 млн руб.

Определить функции темпа роста выручки и эластичности цены относительно спроса.

продукции в месяц. Определить скорость и темп изменения себестоимости при выпуске 20 тыс.шт. и 40 тыс. шт. продукции.

38

7. В среднем расходы на питание y в зависимости от годового дохода х на душу населения описывается функцией y 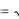2x 40 . Вычислить:

а) скорость изменения расходов на питание при годовом доходе 120 000 руб. и 250 000 руб.; б) полагая, что некоторое время расходы на питание будут изменяться с постоянной скоростью, найти функцию этого изменения.

спроса q (усл.ед.) и темпа роста q, а также вычислить эластичность спроса относительно цены.

предложение уравновешиваются, а также эластичность предложения для этой цены.

11.Функция полных издержек: К = х3 – 6х2 + 15х (ден.ед.). Определить, при каких значениях х (усл.ед.) эластичность полных затрат Ex(K) > 1.

12.Функция спроса от цены имеет вид: q = 100 – p (усл. ед.). Определить, для каких цен спрос эластичен.

спроса от цены и те её значения, при которых спрос относительно цены эластичен.

15. Производственная функция однопродуктовой фирмы, использующей два вида ресурсов – труд (L) и капитал (K) имеет вид: Q = 10 L0,5 K0,5. Найти частные эластичности функции при L = 20 усл. ед.; К = 40 усл. ед.

39

16. Себестоимость продукции С (тыс. руб) описывается функцией

С(х)=0,00025х3+0,0025х2+0,58х+19, 15 x 50 ; где х – объём выпускаемой продукции в месяц. (тыс.ед). Определить, при каком значении х прибыль будет максимальной, если продукция реализуется по цене 2,1 руб. за 1 тыс. ед. Вычислить величину прибыли.

17. Общая сумма расходов на перевозку и хранение деталей на складе определяется формулой С(х)= S q(x) bx / 2 , где х – размер партии деталей; S – затраты на перевозку одной партии; bx/2 – затраты на хранение половины партии (условно средний запас). Определить оптимальный размер партии, при котором расходы будут минимальными. Вычислить это значение при q=50, S=0,2 руб. b=0,1 руб.

18. Ежедневно база обеспечивает потребителей некоторого товара в объёме r=2,5 т. Стоимость хранения h товара на базе равна 0,8 руб за 1т в сутки. Получить товар база может в любом заранее оговоренном количестве и в любое указанное время равными партиями объёма g и через равные промежутки времени Т. Очередной заказ поступает в момент, когда запасы товара становятся

равными 0 . Стоимость хранения запаса g в течение Т суток равна ln gT2 .

Стоимость заказа, независимо от количества привозимого товара, составляет р=100 руб. Определить объём товара, который должна заказывать база, и интервалы его поставки, чтобы суточные затраты были минимальны. При составлении функции суточных затрат учесть, что Т=g/r.

19.Зависимость расхода автомобилем горючего от скорости движения задаётся функцией у=20-0,4х+0,005х2, где у – расход горючего (л) на 100 км пути, х – скорость автомобиля (км/ч). Определить оптимальную скорость автомобиля, при которой расход горючего минимален.

20.Трудоёмкость проектирования микросхем у(х) характеризуется

трудоёмкость её проектирования будет минимальной, и величину соответствующей трудоёмкости.

40

21.Определить оптимальный размер партии и длительность производственного цикла, минимизирующего суммарные затраты из следующих условий:

а) необходимо обеспечить суммарную годовую потребность в 1000 изделий. б) удельные затраты на хранение единицы изделия в течение месяца равны

0,5 руб.

в) производственные затраты на изготовление одной партии равны 10 руб.

22.Функция объёма выпуска продукции для некоторой фирмы имеет вид:

х3 – стоимость оборотных средств. Определить частные эластичности объема выпуска продукции y при х1 = 100 чел; х2 = 100 000 руб; х3 = 10 000 руб.

23. Функция полных издержек двухпродуктовой фирмы задана уравнением C = x2 + 4 y2 + 100, где x и y – объёмы выпуска товаров вида А и В соответственно. Цены этих товаров на рынке равны p1 = 40, p2 = 64. Определить, при каких издержках прибыль достигает максимума.

24.Фирма производит продукцию двух видов в количествах x и y. Функция прибыли задана в виде С = 2x + 4y + 1. Определить, при каких объёмах выпуска продукции достигается максимум прибыли.

25.Урожайность кукурузы z(ц/га) описывается функцией у=15,63х0,372 у0,158, где х (руб./га) – затраты на удобрения и у (руб.) – затраты на семена. Найти:

а) частные коэффициенты эластичности урожайности относительно затрат на удобрение и затрат на семена.

б) значения х и у, при которых прибыль от реализации продукции, выражаемая функцией Р=M у‒ x‒ y‒ k (где – М const – выручка от реализации 1ц кукурузы, к – постоянные затраты, не зависящие от затрат х и у), была бы максимальной .

26. Предполагая, что между переменными х и у существует линейная функциональная зависимость у = ах +b, найти неизвестные значения а и b используя метод наименьших квадратов.

41