Добавил:

ivanov666 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Хабаровский государственный университет экономики и права

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

5667.pdf

Скачиваний:

Добавлен:

13.11.2022

Размер:

2.92 Mб

Скачать

☆

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

3. Степенные ряды

Важным частным случаем функциональных рядов являются степенные ряды. Степенные ряды благодаря их простоте и замечательным свойствам нашли применение практически во всех разделах математики, физики и других наук. Рассматриваемые как предел многочленов при стремлении их степеней к бесконечности, они обладают почти всеми свойствами многочленов с той разницей, что для многих рядов эти свойства выполняются не для всех значений аргумента, а лишь для некоторого ограниченного множества значений.

Определение 7. Функциональные ряды вида

a x

...

xn ...

xn ,

(24)

x x

...

n , (25)

n 0

где а0, а1, а2, ..., аn, ... – постоянные действительные числа (коэффициенты ряда), называются степенными рядами.

Говорят, что ряд (24) расположен по целым неотрицательным степеням переменной x , а ряд (25) – по степеням двучлена x x0 . В (25) x0 – некоторое постоянное число, называемое центром. Нумерации членов этих рядов начинаются с нуля.

Рассматриваемые числовые ряды являются частным случаем функциональных рядов, члены которых имеют, соответственно, следующие виды:

un x an xn , un x an x x0 n .

Члены рядов являются непрерывными и дифференцируемыми функциями на всей числовой оси.

При x0 0 степенной ряд (25) принимает вид (24), поэтому ряд (24) является частным случаем ряда (25). Все последующие рассуждения проще проводить для степенных рядов вида (24). Ряды вида (25) приводятся путём замены переменной

t x x0

(26)

к рядам вида (24) с переменной t . Если ряд (24) сходится на некотором

промежутке X , то ряд (25) будет сходиться в области x : x	x0 X .
Исследуем вид области сходимости степенного ряда (24). Это мно-
жество не является пустым, так как этот ряд сходится при x	0 (сумма ря-
да равна числу a0 ).

Если в (24) переменной x придать определённое значение x1, то получим числовой ряд

a	0	a	x	a	2	x 2	... a	n	x n ...	a	n	x n ,	(27)
	0	1	1		2	1		n	1		n	1
									n	0

который может быть как сходящимся, так и расходящимся.

Определение 8. Если числовой ряд (27) будет сходящимся (расходящимся), то точка x1 будет называться точкой сходимости (расходимости) степенного ряда (27).

Определение 9. Множество значений аргумента x , для которых сходится ряд (24), называют областью сходимости степенного ряда.

В принципе описать область сходимости степенного ряда позволяет теорема Абеля.

Теорема 9 (Абеля). Для степенного ряда (24) имеют место следующие утверждения:

1) если степенной ряд (24) сходится при x x1, то он сходится (при-

том абсолютно) при всех x таких, что х x1 ;

2) если ряд расходится при x x2 , то он расходится при всех x , для которых х x2 .

Доказательство. 1. По условию теоремы числовой ряд (27) сходит-

ся. Следовательно, по необходимому признаку сходимости lim a	x n	0
n	n 1
n

(см. теорему 1 из [7]). Отсюда следует, что сходящаяся числовая последо-

вательность a	x n	ограничена, т.е. найдётся такое число M 0				, что для
	n 1
всех n будет выполняться неравенство
			a	x n	M , n 0,1, 2, ... .
			a	x n	M , n 0,1, 2, ... .
				n 1

Пусть

тогда

величина

и, следовательно,

x n

M qn ,

n 0,1, 2, ...,

т.е.

модуль каждого члена ряда

(24) не превосходит соответствующего члена сходящегося геометрическо-

го ряда

Mqn q

1 . Поэтому, по первому признаку сравнения (см. тео-

рему 3 из [7]) будет сходиться ряд

. Следовательно, при

ряд (24) сходится абсолютно.

2. Дано, что ряд расходится в точке

x x2 ;

нужно доказать, что он

расходится для всех x ,

удовлетворяющих неравенству

. Предпо-

ложим противное: при некотором

x1 ,

удовлетворяющем

неравенству

х1

степенной ряд сходится. Тогда по первой части теоремы Абеля

ряд будет сходиться при всех x ,

для которых

и, в частности, в

точке x2

, что противоречит условию теоремы.

Теорема полностью доказана.

С геометрической

точки

зрения

теореме Абеля утверждается

следующее:

1) если ряд (24) сходится в точке x1

0 , то он абсолютно сходится на

интервале

;

2) если ряд (24) расходится в точке

x2 , то он расходится на луче

, лежащем левее точки

и на луче

, лежащем

правее точки

(см. рисунок).

расходится

сходится

расходится

Для области сходимости степенного ряда (24) возможны следующие ситуации: 1) ряд сходится только в одной точке x 0 (в этой точке сходится всякий степенной ряд (24)); 2) ряд сходится на всей числовой оси; 3) ряд сходится не на всей числовой оси, но и не только в одной точке x 0 .

В третьей ситуации точки сходимости ряда (24) описываются следующей теоремой.

Теорема 10. Если степенной ряд (24) сходится не на всей числовой

оси, но и не только в точке x			0 , то существует число R 0 такое, что:

1)	ряд абсолютно сходится для			x	R ,

2)	ряд расходится при	x	R .

Доказательство. По предположению теоремы множество X сходимости ряда (24) не пусто и ограничено. Его ограниченность следует из теоремы Абеля, поскольку предполагается, что имеется хотя бы одна точка x2 расходимости ряда (тогда точки расходимости удовлетворяют неравенству х x2 , а точки сходимости – х x2 ). У ограниченного множества су-

ществует точная верхняя грань, которую обозначим R R sup X . Число R обладает тем свойством, что в любой его окрестности есть точки, которые как принадлежат множеству X , так и не принадлежат ему. Таким образом, в любой окрестности R есть точки, в которых ряд (24) сходится, а

так же точки, в которых он расходится. Тогда по теореме Абеля при x R
ряд (24) абсолютно сходится, а при x R – расходится.
Теорема доказана.
Определение 10. Число R , введённое в теореме,	называется радиу-
сом сходимости степенного ряда (24). Промежуток	R; R называется

интервалом сходимости степенного ряда (24).

В упоминавшейся ситуации 1) считают, что R 0 (ряд (24) сходится


лишь при x 0 );	в ситуации 2) полагают R		. Следовательно, можно
считать, что радиус сходимости удовлетворяет неравенствам 0 R				.
Остался открытым		вопрос о сходимости степенного ряда (24) на
концах интервала	R, R	, то есть в точках x	R . Общего ответа о схо-

димости ряда в этих точках дать нельзя. В этих точках возможны следующие случаи: 1) ряд расходится в обеих точках; 2) ряд сходится в обеих

точках (в этом случае область сходимости ряда обращается в замкнутый промежуток R, R ; 3) ряд сходится в одной из точек x R и расходится в другой. В каждом конкретном примере надо проводить отдельное исследование поведения степенного ряда на концах интервала R, R .

Замечание 20. Областью сходимости степенного ряда (25) будет либо единственная точка x x0 , либо вся числовая прямая, либо интервал x0 R, x0 R , к которому могут присоединяться один или оба конца. Это следует из замены переменной (26) и утверждений, сформулирован-

ных для ряда (24).

Для отыскания интервала сходимости можно использовать признаки Даламбера или Коши (см. теоремы 6 и 8 из [7]), применённые к ряду, составленному из абсолютных величин членов степенного ряда (24) или (25), т.е. к ряду

или

x )n

n 0

(x 2)n

Пример 19. Найти область сходимости степенного ряда

n 1

Найдём те значения x ,

при которых сходится ряд

2)n

для чего

применим признак Даламбера:

(x 2)n

x 2

n 1

; un

;

un 1

x 2

n 1

x 2

D x

lim

n 1

По признаку Даламбера ряд из абсолютных значений будет сходиться, если D x 1, т.е. если x 2 1. При D x 1 ряд расходится, поэтому ин-

тервал сходимости определяется неравенством

Следовательно,

3 , т.е. интервалом сходимости является интервал 1, 3 .

Исследуем сходимость данного ряда на концах интервала. Подстав-

ляя x

1 в исходный степенной ряд, получим числовой знакопеременный

(

1)n

ряд

лейбницевского типа; он сходится. Абсолютной сходимости

нет, т.к. ряд

1)n

расходится (гармонический ряд). Поэтому

(

n 1 n

(

1)n

ряд

сходится условно. Следовательно, точка x

1 входит в об-

ласть сходимости.

Подставляя x

3 в исходный степенной ряд,

получим числовой ряд

2)n

. Это гармонический ряд, он расходится, поэтому точка

1 n

3 не входит в область сходимости.

Окончательно получаем, что область сходимости исследуемого сте-

пенного ряда есть полуотрезок [1,

3) ,

причём сходимость ряда в точке

1 условная.

х2n

Пример 20. Найти область сходимости степенного ряда n

Применим радикальный признак Коши:

x 2n

x 2

K x

lim n

lim

По признаку Коши

ряд сходится, если

K x

1 ,

и расходится, если

K x

1. Следовательно,

неравенство

х2

1 определяет интервал сходи-

мости.

Отсюда

4 ,

т.е.

Следовательно,

на

интервале

(

2, 2) исходный ряд сходится.

Исследуем сходимость ряда на концах интервала. Подставляем значение x 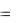2 в исходный ряд, получим:

(

2)2n

n 0 4n

n 0

Для этого ряда не выполняется необходимый признак сходимости:

lim un

lim 1 1

0 .

Ряд

1 расходится, и точка x

2 не входит в область сходимости ис-

ходного степенного ряда.

При x 2 получим ситуацию, аналогичную случаю x 2 . Поэтому

2 также не входит в область сходимости.

Окончательно получаем, что область сходимости степенного ряда

х2n

есть интервал ( 2, 2) .

0 4n

Пример 21. Найти область сходимости ряда

n!(x 3)n . Применим

n 0

признак Даламбера для отыскания интервала сходимости:

3)n

n ;

3)n

n 1 ;

n !(x

n !

un 1

1)!(x

1)!

n 1

D x

lim

un 1

lim

1)!

lim

n !(n

n !

x 3

n !

x 3

при

lim n 1

при

3 0,

Таким образом, ряд сходится абсолютно только при x 3, а в остальных точках числовой прямой ряд расходится.

Пример 22. Найти область сходимости степенного ряда

	3n	1 (x 1)n	.
n 1		nn

Воспользуемся предельным (радикальным) признаком Коши:

n 1

3n 1

1) n

lim n

3 n

K x

lim

n n

lim

Таким образом, имеем K x

1 при любом значении x , т.е. ряд схо-

дится на всей числовой оси (

) .

Замечание 21. Из примеров 21

видно,

что

если

D x

( K x

т.е.

R 0 ,

то

область

сходимости

степенного

ряда

(x x

состоит

из

одной точки

x .

Если

же

D x

n 0

( K x 0 ), т.е. R , то степенной ряд сходится на всей числовой оси. Замечание 22. Для вычисления радиуса сходимости R степенного

ряда можно использовать такие формулы:

R	lim	an		,		(28)
R	lim	an 1		,		(28)
	n	an 1
R	lim	1			.	(29)



	n	n	a
			n

Они являются следствиями применения признаков Даламбера и Коши при отыскании интервала сходимости (см. приведённые выше примеры).

Пример 23. Найти области сходимости степенных рядов:

а)

; б)

;

в)

(nx)n ;

1 n

n 0 n!

n 1

а) в данном случае an

an 1

. Поэтому, применяя форму-

n 1

лу (28), получаем R lim

lim

lim 1

1. Этот ряд ви-

an 1

да (24). Следовательно, интервал сходимости

R, R

1; 1 .

Исследуем ряд на концах интервала. При x

1 получаем ряд

1 n . Данный ряд условно сходится (см. пример 19). Таким образом,

n 1 n

точка x 1 входит в область сходимости.

При x

1 получаем гармонический ряд

, он расходится. Таким

1 n

образом, точка x

1 не входит в область сходимости.

Окончательно имеем, что областью сходимости

степенного ряда

является полуотрезок [

1, 1)

;

n 1 n

б) так как an

, an

, то по формуле (28) получаем, что

1)!

R lim

lim

1)!

lim

n!(n 1)

lim (n 1)

an 1

Следовательно, данный степенной ряд сходится абсолютно на всей

числовой прямой;

в) так как a

nn , то по формуле (29) имеем:

lim

0 .

n nn

Следовательно, данный ряд сходится только в одной точке x

0 .

Определение 11. Каждому значению х из области сходимости степенного ряда (24) соответствует определённое значение величины

S (x)	an xn ,
n	0

которую называют суммой степенного ряда.

Изучим свойства степенных рядов. Так как степенные ряды являются частным случаем функциональных рядов, то к ним можно применять теоремы 5 – 8, приведённые в пункте 1, для функциональных рядов. Сформулируем и докажем эти теоремы для степенного ряда (24). При этом считаем, что R 0 (при R 0 дальнейшие теоремы бессодержательны или тривиальны).

Теорема 11. Степенной ряд (24) с радиусом сходимости

R равно-

мерно сходится на любом отрезке

r, r

, содержащемся

интервале

сходимости.

Доказательство. Так как r

R , то при x

r степенной ряд (24)

схо-

дится абсолютно, то есть сходится ряд

r n . Для любого x из

r, r

r n , т.е.

выполняется неравенство

r .

Тогда

an xn

сте-

пенной ряд (24) является мажорируемым на отрезке

r, r . Следователь-

но, по теореме 5 (признаку Вейерштрасса) он равномерно сходится на этом отрезке.

Теорема 12. Сумма S (x) степенного ряда (24) есть непрерывная

функция на интервале сходимости	R, R .
Доказательство. При любом	x из R, R		можно выбрать число

r 0 таким, чтобы выполнялись неравенства		x	r R . Согласно теоре-

мам 11 и 6 сумма S (x) будет непрерывной в точке x .

Замечание 23. Справедливо более общее, чем в теореме 12, утверждение. Оно состоит в том, что сумма ряда (24) непрерывна на всём промежутке его сходимости. Промежутками же сходимости, как отмечалось

выше, могут быть и R, R ,	R, R ,	R, R ,				,	.
Теорема 13. Степенной ряд (24) можно почленно интегрировать по
любому отрезку a, b , лежащему внутри интервала сходимости								R, R .
Доказательство. Пусть					.	Тогда по условию теоремы
	r max	a	,	b
r R и по теореме 11 ряд равномерно сходится на							r, r . Следовательно,
он сходится равномерно и на отрезке		a, b , так как отрезок a, b						r, r
(см. замечание 1). Поскольку все члены un x						an xn ряда непрерывны на
a, b , то утверждение этой теоремы следует теперь из теоремы 7.
Пример 24. Проинтегрируем степенной ряд (24) по переменному
промежутку 0, x , где 0 x	R . Для членов этого ряда по формуле Нью-
тона – Лейбница имеем:

n 1

ant

(подстановка нижнего предела t

0 даёт нуль). Учитывая это, для суммы

S (x) степенного ряда (24) из теоремы 13 следует равенство

S t dt

ant

n 0 n 1

0 n 0

n 0 0

При R x

0 интегрирование проводится по отрезку

x, 0 , а затем

обе части равенства умножаются на

1 .

Таким образом, внутри интервала сходимости степенного ряда (24)

справедливо равенство

n 1

S t dt

0 n 1

где S (x) an xn . Полученный в результате интегрирования ряд снова

является степенным рядом.

Пример 25. Рассмотрим степенной ряд

1 n xn 1 x x2 x3

1 n xn

n 0

радиус сходимости которого, очевидно, равен единице. Ясно, что в точках x 1 и x 1 этот ряд расходится. Таким образом, областью сходимости этого ряда является интервал 1,1 . Сумма этого геометрического ряда

есть функция S(x)			1		. По теореме 13 для каждого x из																1,1 имеем

			1	x
x 1		dt	x 1 t t 2			t3				dt x					x2			x3		x4	,
		dt	x 1 t t 2			t3				dt x											,
01	t		0													2		3	4
откуда вытекает равенство
			ln 1		x x		1	x	2		1	x	3	1		x	4		.

							2				3			4
							2				3			4

Теперь наряду с рядом (24) рассмотрим ряд

a	2a	2	x	3a x2	n 1 a	n	1	xn	,	(30)
1		2		3		n	1

составленный из производных членов исходного ряда. Ряд (30) снова является степенным. Если областью сходимости ряда (24) является интервал 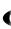R, R , то можно доказать, что ряд (30) сходится на том же интервале. Тогда по теореме 11 оба ряда будут равномерно сходящимися на любом отрезке r, r , содержащемся в интервале R, R . Тогда по теореме 8 возможно дифференцирование ряда (24) (члены рядов (24) и (30) являются непрерывными функциями). Сформулируем сказанное.

Теорема 14. Степенной ряд (24) можно дифференцировать в любой точке интервала сходимости, причём справедливо равенство

d	an xn	n 1 an 1xn .

dx
dx	n 0	n 0

Теорему 14 можно применить для нахождения сумм некоторых степенных рядов.

Пример 26. Требуется найти сумму степенного ряда

1 2x	3x2	n 1 xn	n 1 xn .
		n	0
Наряду с рядом рассмотрим степенной ряд
1	x x2 x3	xn	xn .
		n	0

Последний ряд является геометрическим рядом со знаменателем q x и первым членом, равным единице. Геометрический ряд сходится только при x 1, т.е. радиус сходимости этого степенного ряда равен единице. По

формуле (11) из [7] сумма этого ряда есть функция		S(x)			1	:

					1 x
1 x x2 x3	xn	1		.


	1		x

Продифференцировав этот ряд, получим следующее:

1 2x 3x2	n 1 xn	1	1		1	1	.

		1 x		1 x 2		x 2
					1

<<< < Предыдущая 1 23 / 83 4 5 6 7 8 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
13.11.20222.72 Mб15662.pdf
#
13.11.20222.81 Mб25663.pdf
#
13.11.20222.82 Mб65664.pdf
#
13.11.20222.86 Mб85665.pdf
#
13.11.20222.89 Mб15666.pdf
#
13.11.20222.92 Mб25667.pdf
#
13.11.20222.96 Mб45668.pdf
#
13.11.20222.96 Mб25669.pdf
#
13.11.20223.01 Mб15670.pdf
#
13.11.20223.01 Mб15671.pdf
#
13.11.20223.03 Mб35672.pdf