
- •Введение
- •1. Основные понятия и утверждения о функциональных рядах
- •2. Упражнения и вопросы для самопроверки
- •3. Степенные ряды
- •4. Упражнения и вопросы для самопроверки
- •5. Ряды Тейлора и Маклорена
- •6. Упражнения и вопросы для самоконтроля
- •7. Применение степенных рядов в приближённых вычислениях
- •8. Упражнения и вопросы для самопроверки
- •9. Ряды Фурье
- •10. Упражнения и вопросы для самопроверки
- •Библиографический список
- •Содержание
Министерство образования и науки Российской Федерации
Государственное образовательное учреждение высшего профессионального образования
«Хабаровская государственная академия экономики и права»
Кафедра математики и математических методов в экономике
М.Ф. Тиунчик, Е.О. Старкова, С.В. Тонконог
Математический анализ
Функциональные ряды
Хабаровск 2011
ББК В Т 45
Тиунчик М. Ф. Математический анализ. Функциональные ряды : учеб. по-
собие / |
М. Ф. Тиунчик, Е. О. Старкова, С. В. Тонконог. – Хабаровск : |
РИЦ |
ХГАЭП, 2011. – с. |
Содержание учебного пособия соответствует государственным образовательным стандартам дисциплины «Математический анализ» по изучению раздела «Числовые и функциональные ряды». Перед изучением данного пособия необходимо ознакомиться с учебным пособием авторов [7]. Для выполнения индивидуальных заданий по данной тематике можно использовать методическую разработку авторов [8].
Пособие предназначено для бакалаврантов и магистрантов по направлениям подготовки «Экономика», «Менеджмент», «Торговое дело», «Сервис», «Туризм», «Государственное и муниципальное управление», «Товароведение», «Прикладная информатика».
Рецензенты: А. И. Ивлева, канд. физ.-мат. наук, доцент Хабаровского пограничного института Федеральной службы Российской Федерации;
Е. В. Карачанская, канд. физ.-мат. наук, доцент кафедры прикладной математики ТОГУ
Утверждено издательско-библиотечным советом академии в качестве учебного пособия
Тиунчик М.Ф, Старкова Е.О., Тонконог С.В., 2011 Хабаровская государственная академия экономики и права, 2011
2
Введение
Данное учебное пособие является продолжением работы [7] авторов и посвящено изучению теории рядов – важнейшего раздела дисциплины «Математический анализ». В нём на базе дифференциального и интегрального исчислений функции одной действительной переменной и на основе знаний материала по числовым рядам излагается теория функциональных рядов.
В первом параграфе приведены основные понятия и утверждения, описаны поточечная и равномерная сходимости функциональных рядов, рассмотрены вопросы непрерывности суммы ряда, почленного дифференцирования и интегрирования. В последующих параграфах на этой основе изучаются степенные и тригонометрические ряды, ряды Тейлора и Фурье. В отдельном параграфе показано применение теории степенных рядов в приближённом вычислении значений функции и определённых интегралов, при нахождении решений обыкновенных дифференциальных уравнений.
По всем темам имеются подробные теоретические сведения, большинство утверждений приведено с доказательством. Доказательства опущены лишь в тех случаях, когда требуются дополнительные знания из математического анализа, выходящие за рамки государственных образовательных стандартов для бакалаврантов по указанным в аннотации направлениям подготовки. Напоминаются все основные понятия из предыдущих изученных разделов дисциплины «Математичекий анализ».
Теоретический материал сопровождается рассмотрением разнообразных примеров, поясняющих введённые определения и полученные выводы. Приведено значительное число замечаний, уточняющих применяемые понятия и утверждения. Эти замечания в основном предостерегают читателя от возможных неправильных заключений.
Каждый параграф сопровождается набором задач для аудиторной и самостоятельной работы. Имеется также список теоретических вопросов для самоконтроля. Студент может считать материал усвоенным, если смо-
3

жет выполнять предложенные упражнения и отвечать на вопросы для самоконтроля.
В пособии принята сплошная нумерация отдельно для определений, теорем, замечаний и примеров в теоретической части. В упражнениях и вопросах для самопроверки к каждой теме проведена отдельная нумерация.
Пособие рассчитано на студентов очной и заочной форм обучения и может быть использовано преподавателями при проведении практических занятий.
1. Основные понятия и утверждения о функциональных рядах
Сначала изучим функциональные последовательности. Рассмотрим последовательность
f1 x , f2 x , ... , fn x , ..., |
(1) |
членами (элементами) которой являются функции одной действительной переменной x . Последовательности вида (1) называются функциональ-
ными.
Чаще всего встречаются такие функциональные последовательности, члены которых задаются одной и той же формулой (аналитическим выра-
жением). В этом случае fn x |
называют общим членом последователь- |
ности (1). Каждая из функций |
fn x n 1, 2, ... может иметь свою область |
определения X n . Тогда последовательность (1) считается заданной на од-
ном и том же множестве X , |
являющемся пересечением множеств X n |
X X n . Обычно в качестве |
X будут фигурировать некоторые проме- |
жутки числовой оси (отрезки, полуотрезки, интервалы, лучи) или вся числовая ось.
При некотором x0 из X функциональная последовательность (1)
обратится в числовую последовательность |
|
f1 x0 , f2 x0 , ... , fn x0 , ..., |
(2) |
4

которая может как сходиться, так и расходиться (см. [7]). Пусть последова-
тельность (2) сходится, тогда lim |
fn x0 |
f x0 , где f x0 |
– некоторое |
|
n |
|
|
|
|
число. |
|
|
|
|
Определение 1. Функциональная |
последовательность |
fn x |
назы- |
|
вается сходящейся на некотором |
промежутке D X , если |
она |
сходит- |
|
ся как числовая последовательность при каждом значении x из этого промежутка.
Если это определение выполняется, то значение предела зависит от
x , т.е. является функцией, определённой на D . Тогда можно сказать, |
что |
|
на D функциональная последовательность (1) имеет пределом некоторую |
||
функцию f |
x : |
|
|
lim fn x f x . |
(3) |
|
n |
|
Функция f |
x называется предельной функцией функциональной после- |
|
довательности (1) в области D . |
|
|
В этой ситуации говорят о поточечной сходимости fn x к f |
x . |
|
Далее будет рассмотрен и другой тип сходимости функциональной последовательности.
Естественно выяснить свойства предельной функции – её непрерывность, дифференцируемость, интегрируемость. Функциональные свойства f x , как будет изложено ниже, зависят не только от свойств членов последовательности (1), но и от характера их приближения к предельной функции.
Пример 1. Пусть fn |
x |
1 |
|
x |
n |
, т.е. функциональная последова- |
||||
|
|
|
|
|||||||
|
n |
|
||||||||
|
|
|
|
|
|
|
|
|
||
тельность имеет вид |
|
|
|
|
|
|
|
|
|
|
|
x |
1 |
|
x |
2 |
|
x |
3 |
||
1 |
|
, |
1 |
|
|
|
, |
1 |
|
, .... |
1 |
2 |
|
3 |
|||||||
|
|
|
|
|
|
|
||||
Все её члены определены и непрерывны на  ,
,  . Из второго замечательного предела следует, что
. Из второго замечательного предела следует, что
5

|
|
x |
n |
|
lim fn x |
lim 1 |
|
e x , |
|
n |
||||
n |
n |
|
т.е. f x ex . Предельная функция ex также определена и непрерывна на всей числовой оси.
ex . Предельная функция ex также определена и непрерывна на всей числовой оси.
Пример 2. Рассмотрим последовательность
1 |
|
, |
1 |
|
, |
1 |
|
, |
, |
1 |
|
, |
, |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
1 |
x |
2 |
|
x |
3 |
|
x |
n |
|
|
|||
члены которой имеют различные области определения, на отрезке |
0,1 , |
||||||||||||||
где определены все члены. Для всех x из |
0,1 |
верно равенство |
|
||||||||||||
|
lim |
fn |
x |
lim |
|
1 |
0 . |
|
|
||||||
|
|
|
|
|
|||||||||||
|
x |
n |
|
|
|||||||||||
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
||
Поэтому предельной функцией этой последовательности на отрезке |
0,1 |
||||||||||||||
является функция, тождественно равная нулю на 0,1 : |
|
||||||||||||||
|
|
|
|
f x |
0, 0 |
|
x |
1. |
|
|
|
|
|||
Все функции этой последовательности на отрезке |
0,1 непрерывны. Пре- |
||||||||||||||
дельная функция является постоянной, она также непрерывна на 0,1 . Пример 3. Требуется найти предельную функцию последовательно-
сти x, x2 , ... , xn , ... на отрезке 0,1 . Для всех 0 x 1 имеем, что
lim xn 0 .
n
Если x 1, то имеем последовательность, состоящую из единиц; её предел будет равен единице. Таким образом,
f |
x |
0, если 0 |
x |
1; |
1, если x |
1. |
|
||
|
|
|
||
Предельная функция f x |
разрывна на |
0,1 . |
Она имеет разрыв первого |
|
рода в точке x 1, хотя все члены функциональной последовательности fn x xn непрерывны на данном отрезке.
xn непрерывны на данном отрезке.
Пример показывает, что непрерывная на некотором промежутке D последовательность функций может сходиться к функции, имеющей на данном промежутке разрывы.
6

Пусть для функциональной последовательности (1) при всех x |
из |
||||||||||||
некоторого промежутка D имеет место равенство (3). |
|
|
|||||||||||
Тогда можно сказать следующее: при каждом фиксированном x |
x0 |
||||||||||||
из промежутка D для любого заданного |
|
0 найдётся такой номер N |
, |
||||||||||
что для всех n |
N будет выполняться неравенство |
|
|
||||||||||
|
|
|
|
fn x0 |
f x0 |
|
. |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
Если взять другое значение x |
x1 из D , |
то даже для того же |
но- |
||||||||||
мер N , после которого будет выполнено неравенство |
|
|
|||||||||||
|
|
|
|
fn x1 |
f x1 |
|
, |
|
|
|
|||
|
|
|
|
|
|
|
|
||||||
вообще говоря, будет другим. |
|
|
|
|
|
|
|
|
|||||
Таким образом, номер N , после которого выполняется неравенство |
|||||||||||||
|
|
|
|
|
fn x |
f x |
|
, |
|
|
(4) |
||
|
|
|
|
|
|
|
|
||||||
зависит и от |
, и от x |
N N |
, x . |
Возникает вопрос, существует ли та- |
|||||||||
кой номер N , который при заданном |
|
|
0 пригоден для всех x из проме- |
||||||||||
жутка D . Оказывается, что для некоторых функциональных последова- |
|||||||||||||
тельностей такой номер существует, а для других – нет. |
|
|
|||||||||||
Определение 2. Функциональная последовательность fn x , имею- |
|||||||||||||
щая на промежутке D предельную функцию f |
x , называется равномер- |
||||||||||||
но сходящейся к f x |
на D , |
если для любого |
0 можно указать такой |
||||||||||
не зависящий от x номер N |
, что при всех n |
N |
неравенство (4) вы- |
||||||||||
полняется для всех x из D . |
|
|
Неравенство (4) равносильно неравенствам |
|
|
f x |
fn x f x |
. |
Поэтому определение 2 геометрически означает, что графики функций fn x , начиная с некоторого номера, полностью расположены в полосе
ширины 2 , ограниченной графиками функций f x |
и |
f x |
(гра- |
фики этих последних функций получаются смещением на |
вниз и на |
||
вверх графика функции f x ). |
|
|
|
Отметим, что равномерная сходимость влечёт поточечную сходимость: если fn x сходится к f x
сходится к f x равномерно на D , то для любой точки
равномерно на D , то для любой точки
7

x0 из D справедливо равенство |
lim |
fn |
x0 f |
x0 . Обратное утвержде- |
||||||
|
|
|
|
|
|
n |
|
|
|
|
ние неверно. |
|
|
|
|
|
|
|
|
|
|
Если все функции |
fn x |
|
и |
f x |
непрерывны на D , то равномерная |
|||||
сходимость означает, что при n |
|
|
|
|
|
|||||
|
|
|
|
|
|
0. |
(5) |
|||
|
|
max |
fn x |
f x |
|
|||||
|
|
x D |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Геометрически max |
fn x |
f |
x |
|
означает наибольшее расстояние между |
|||||
x D |
|
|
|
|
|
|
|
|
|
|
графиками функции fn x |
и функции f x |
|
на промежутке D . |
|||||||
Если условие (5) не выполнено, то сходимость последовательности |
||||||||||
fn x к f x
к f x не является равномерной.
не является равномерной.
Приведённые геометрические интерпретации позволяют по графикам функций fn x и f x
и f x (без аналитических доказательств выполнения неравенства (4)) выяснить, является ли последовательность fn x
(без аналитических доказательств выполнения неравенства (4)) выяснить, является ли последовательность fn x равно-
равно-
мерно или неравномерно сходящейся к предельной функции f x на некотором промежутке.
на некотором промежутке.
Пример 4. Покажем, что функциональная последовательность из примера 2 равномерно сходится на отрезке 0,1 . Так как согласно примеру 2 предельная функция на этом промежутке равна нулю, то при любом вы-
бранном |
0 надо найти такой номер N |
, после которого для всех x из |
||||||||||||||||||||||||
0,1 |
|
выполнялось бы неравенство (4). В данном случае это неравенство |
||||||||||||||||||||||||
имеет вид |
|
1 |
|
|
0 |
|
или |
|
|
1 |
|
. Так как 0 x |
1 и x |
n n , то оче- |
||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
x |
|
n |
|
|
|
|
x |
|
n |
|
|
|
|
|
|
|
||||
видны неравенства |
0 |
|
1 |
|
|
|
1 |
. Если потребовать, чтобы выполнялось |
||||||||||||||||||
x |
n |
|
n |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
неравенство |
1 |
|
, то |
будет |
|
выполняться |
|
|
и |
нужное |
неравенство |
|||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||
|
n |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
0 |
|
|
. |
|
Для |
выполнения |
|
неравенства |
1 |
|
необходимо, |
чтобы |
|||||||||||
|
1 |
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
||||
n |
1 |
. Отсюда |
|
видно, что в |
качестве |
N |
можно взять |
целое |
число |
|||||||||||||||||
|
|
|||||||||||||||||||||||||
8

N |
1 |
|
|
1, где |
1 |
– целая часть числа |
1 |
. Таким образом, номер N |
|||
|
|
|
|
|
|
||||||
зависит только от |
и не зависит от значения x из отрезка 0,1 . Проведе- |
||||||||||
но |
аналитическое |
|
доказательство того, |
|
что |
последовательность |
|||||
fn x |
1 |
|
равномерно сходится на отрезке 0,1 |
к своей предельной |
|||||||
|
|
|
|
|
|||||||
|
|
|
|
|
|||||||
|
|
x |
n |
|
|
|
|
|
|||
функции f |
x 0 . |
|
|
|
|
|
|||||
|
Замечание 1. Если fn x сходится равномерно к f x на промежут- |
||||||||||
ке D , то она равномерно сходится к этой функции на любом промежутке |
|||||||||||
D* |
D . Так, рассмотренная в последнем примере последовательность бу- |
||||||||||
дет равномерно сходиться к f x 0 на любом промежутке, являющемся частью отрезка 0,1 .
0 на любом промежутке, являющемся частью отрезка 0,1 .
Пример 5. Покажем, что последовательность |
fn x |
xn из примера |
3 не является равномерно сходящейся на отрезке |
0,1 . |
Сначала её рас- |
смотрим на полуотрезке 0,1 . Из примера 3 известно, что на этом промежутке предельная функция f x есть тождественный нуль. При фиксиро-
есть тождественный нуль. При фиксиро-
ванном n имеем: xn 1, если x 1 . Если изобразить графики функций
x , x2 , x3 , … на этом полуотрезке, то станет наглядно видно, что при |
1 |
их графики не попадают в нужную полосу, а именно полосу, ограниченную прямыми y 0  и y 0
и y 0  (см. геометрическую интерпретацию
(см. геометрическую интерпретацию
равномерной сходимости). Это значит, что последовательность fn x xn
xn
на полуотрезке 0,1 сходится к предельной функции f |
x 0 неравномер- |
но. Тем более нет равномерной сходимости и на отрезке |
0,1 . |
Замечание 2. Равномерная сходимость последовательности к предельной функции существенно зависит от множества, на котором функциональная последовательность рассматривается. Одна и та же функциональная последовательность на одном множестве может сходиться равномерно, а на другом – неравномерно. Например, только что рассмотренная в
примере 5 последовательность fn x xn на отрезке |
0, |
1 |
будет равно- |
|
2 |
||||
|
|
|
9

мерно сходиться к своей предельной функции на этом отрезке (попрежнему f x 0 ). Это легко можно проверить геометрически путём по-
0 ). Это легко можно проверить геометрически путём по-
строения графиков функций x , x2 , x3 , … на отрезке 0, 12 .
Замечание 3. Если нет равномерной сходимости на некотором промежутке, то её нет и на любом промежутке, его содержащем (это уже отмечалось в примере 5).
Если равномерной сходимости на некотором промежутке нет, то на некоторой его части она может быть (см. замечание 2).
Если равномерная сходимость наблюдается на некотором промежутке, то могут быть промежутки, его включающие, на которых её нет (см. пример 5 и замечание 2).
Сделанные выводы, естественно, дополняются замечанием 1.
Пример 6. Рассмотрим на всей числовой оси |
, |
последова- |
||||
тельность непрерывных функций fn |
x |
|
nx |
. Очевидно, что на этом |
||
|
|
|||||
|
n2 x2 |
|||||
|
1 |
|
|
|
||
множестве её предельной функцией будет непрерывная функция f x 0 . Выясним, является ли эта последовательность равномерно сходящейся на отрезке 0,1
0 . Выясним, является ли эта последовательность равномерно сходящейся на отрезке 0,1 к своей предельной функции, которой является тождествен-
к своей предельной функции, которой является тождествен-
ный нуль |
на этом отрезке. |
Возьмём точку x |
|
1 |
, |
которая |
при |
всех |
||||||
|
||||||||||||||
|
|
|
|
|
|
|
n |
|
|
|
|
|
||
n |
1, 2, 3, ... |
принадлежит данному отрезку. Очевидно, |
что fn |
1 |
|
1 |
. При |
|||||||
n |
2 |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
малых |
1 |
ни одна |
из функций fn x |
не |
попадёт |
в полосу |
||||||||
|
|
|||||||||||||
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
0 |
, 0 |
для всех значений x от 0 до 1 (ни одна из кривых данной по- |
||||||||||||
следовательности не примыкает к оси Ox полностью на всём протяжении отрезка от 0 до 1). Это не входит в противоречие с тем, что f x 0 на 0,1 , так как по каждой вертикали, взятой в отдельности, точки кривых с увеличением n приближаются к оси Ox , т.е. к прямой y 0 ; иными сло-
0 на 0,1 , так как по каждой вертикали, взятой в отдельности, точки кривых с увеличением n приближаются к оси Ox , т.е. к прямой y 0 ; иными сло-
вами, имеется поточечная сходимость fn x к f x |
0 . Итак, последова- |
тельность fn x сходится к f x 0 неравномерно на |
0,1 . |
10

Для функций fn x из примера 6 легко установить, что точка |
x |
1 |
|
||||||||||
|
|
||||||||||||
n |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||
из отрезка |
0,1 |
|
будет точкой максимума при всех n 1. При этом все |
||||||||||
|
1 |
|
1 |
|
|
|
1 |
. Таким образом, |
|
||||
ymax fn |
|
. Поэтому max |
fn x |
f x |
не вы- |
||||||||
n |
2 |
2 |
|||||||||||
|
x 0,1 |
|
|
|
|
|
|
||||||
полняется условие (5) и имеем ещё одно подтверждение неравномерной сходимости.
В этом примере «горбы» всех кривых fn x |
высоты |
1 |
смещаются |
|||
2 |
||||||
|
|
|
|
|
||
вместе с точками x |
1 |
к оси ординат. |
|
|
|
|
n |
|
|
|
|||
|
|
|
|
|
||
Читателю рекомендуем выяснить, может ли функциональная последовательность примера 6 сходиться равномерно к предельной функции f x 0 на каких-нибудь промежутках числовой оси и на всей числовой оси.
0 на каких-нибудь промежутках числовой оси и на всей числовой оси.
Теперь без доказательства сформулируем основные свойства предельной функции функциональной последовательности.
Теорема 1. Предельная функция f x равномерно сходящейся функциональной последовательности непрерывных функций fn x
равномерно сходящейся функциональной последовательности непрерывных функций fn x на некотором промежутке D есть непрерывная на этом промежутке функция.
на некотором промежутке D есть непрерывная на этом промежутке функция.
Замечание 4. Требование равномерной сходимости последовательности, составленной из непрерывных функций, фигурирует в этой теореме как достаточное условие непрерывности предельной функции, но оно не является необходимым условием.
Приведём примеры неравномерно сходящихся последовательностей непрерывных на некотором промежутке функций к непрерывной на нём
функции. |
Простейшим примером |
является последовательность |
|||
fn x 1 |
x |
n |
|
|
|
|
непрерывных на |
, |
функций из примера 1. Хотя |
||
n |
|||||
|
|
|
|
||
эта последовательность на  ,
, 
 не является равномерно сходящейся к предельной функции f x
не является равномерно сходящейся к предельной функции f x ex , последняя является непрерывной функцией на всей числовой оси.
ex , последняя является непрерывной функцией на всей числовой оси.
11
В качестве ещё одного примера можно привести неравномерно сходящуюся на отрезке 0,1 последовательность непрерывных функций из примера 6 с непрерывной на этом отрезке предельной функцией f x
последовательность непрерывных функций из примера 6 с непрерывной на этом отрезке предельной функцией f x 0 .
0 .
Замечание 5. Если все функции функциональной последовательности непрерывны на некотором промежутке, а её предельная функция на этом промежутке имеет разрывы, то это означает, что функциональная последовательность сходится к ней неравномерно на промежутке (это утверждение иллюстрирует пример 5).
Теорема 2. Если функции fn x непрерывны на a, b
непрерывны на a, b и равномерно сходятся на этом отрезке к функции f x
и равномерно сходятся на этом отрезке к функции f x (непрерывной на a, b
(непрерывной на a, b по теоре-
по теоре-
ме 1), то предельная функция интегрируема на a, b . При этом числовая
b |
|
|
|
|
|
|
b |
последовательность fn |
x dx |
|
сходится к интегралу |
f x dx , т.е. имеет |
|||
a |
|
|
|
|
|
|
a |
место равенство |
|
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
lim |
|
fn |
x dx |
f |
x dx . |
(6) |
n |
a |
|
|
a |
|
|
|
|
|
|
|
|
|
||
Замечание 6. Так как lim |
fn x |
f x |
, то равенство (6) можно пе- |
||||
|
n |
|
|
|
|
|
|
реписать в виде |
|
|
|
|
|
|
|
|
b |
|
|
b |
|
|
|
lim |
f n |
|
x dx |
lim |
f x dx , |
|
|
n |
a |
|
|
a |
n |
|
|
в котором переставлены знаки предела и интеграла. Следовательно, равенство (6) означает, что допустим предельный переход под знаком интеграла.
Замечание 7. В этой теореме, как и в теореме 1, условие равномерной сходимости последовательности является лишь достаточным, но не будет необходимым. Предельная функция неравномерно сходящейся последовательности так же может быть интегрируемой (см. пример 6).
Замечание 8. Требование непрерывности функций fn x в теореме 2 можно заменить на требование их интегрируемости в промежутке a, b .
в теореме 2 можно заменить на требование их интегрируемости в промежутке a, b .
12

Теорема 3. Пусть выполняются следующие условия: |
|
|
||||||||||||
1) все функции |
|
fn x |
непрерывно |
дифференцируемы |
на отрезке |
|||||||||
a, b , т.е. функции fn x |
непрерывны на |
a, b ; |
|
|
|
|||||||||
2) последовательность |
fn x |
сходится хотя бы в одной точке x0 от- |
||||||||||||
резка a, b к числу f |
x0 |
; |
|
|
|
|
|
|
|
|
|
|
||
3) последовательность |
fn x |
|
равномерно сходится на a, b к неко- |
|||||||||||
торой предельной функции g x . |
|
|
|
|
|
|
|
|
|
|||||
Тогда верны следующие утверждения: |
|
|
|
|||||||||||
1) функциональная последовательность сходится на |
a, b |
равномер- |
||||||||||||
но к своей предельной функции |
f |
x |
; |
|
|
|
|
|
|
|||||
2) предельная функция |
f |
x |
последовательности |
fn x |
дифферен- |
|||||||||
цируема, причём |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f |
|
x |
g x . |
|
|
|
|
(7) |
|
Замечание 9. Так как по условию теоремы |
|
|
||||||||||||
|
|
|
|
|
lim |
fn |
x |
g x , |
|
|
|
|||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
то равенство (7) имеет вид |
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
f |
x |
|
|
lim fn x . |
|
|
|
|||
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
Последнее можно переписать так: |
|
|
|
|
|
|
|
|
||||||
|
d |
|
lim |
fn x |
lim |
d |
|
fn x , |
|
|
||||
|
dx |
dx |
|
|
||||||||||
|
n |
|
|
|
n |
|
|
|
|
|||||
где d есть знак производной. Следовательно, в утверждении (7) речь идёт dx
о перестановке знаков предела и производной.
Замечание 10. По поводу третьего условия теоремы 3 справедливо такое замечание, как и в теоремах 1 и 2 (см. замечания 4 и 7).
Теперь перейдём к изучению функциональных рядов. Определение 3. Выражение вида
u1 x u2 x |
un x |
un x , |
(8) |
|
n |
1 |
|
13

состоящее из суммы членов бесконечной функциональной последовательности un x функций действительной переменной x , заданных на одном и том же множестве X , называется функциональным рядом.
функций действительной переменной x , заданных на одном и том же множестве X , называется функциональным рядом.
Функции un x , из которых образовано выражение (8), называются членами функционального ряда. В основном рассматриваются ряды, ко-
гда n -й член un x задаётся для всех n единой формулой. Тогда un x |
бу- |
||
дем называть общим членом ряда (8). |
|
|
|
Если задать некоторую точку x0 |
из X , то получим числовой ряд |
|
|
u1 x0 u2 x0 |
un x0 |
, |
(9) |
который может как сходиться, так и расходиться. Если ряд (9) сходится, то говорят, что функциональный ряд (8) сходится в точке (речь идёт о поточечной сходимости ряда (8)). Такая сходимость определена в [7] (см. определение 3). Она означает, что существует конечный предел
|
lim Sn x0 S x0 , |
|
n |
где Sn x0 u1 x0 |
un x0 есть n -я частичная сумма ряда (9). Число |
S x0  является суммой числового ряда (9).
является суммой числового ряда (9).
Определение 4. Множество D всех значений x из X , при которых ряд (8) сходится, называется областью сходимости функционального ряда (8).
Название «область сходимости» оправдывается тем, что множество D чаще всего будет являться некоторым промежутком числовой оси или всей числовой осью  ,
,  .
.
При изменении в D переменной x будет меняться сумма ряда (8). Тем самым в области D сходимости ряда будет определена функция S x ,
называемая суммой функционального ряда (8). |
|
||||
Пусть |
|
|
|
|
|
|
|
Sn x |
u1 x |
un x |
(10) |
есть n -ая |
частичная |
сумма |
ряда (8), а rn x |
есть сумма остатка |
|
un 1 x un |
2 x |
этого ряда. Тогда в области |
D имеем следующие |
||
равенства: |
|
|
|
|
|
|
|
S x |
Sn x |
rn x , |
(11) |
14

lim rn x 0 , |
(12) |
|
n |
|
|
S x |
lim Sn x . |
(13) |
|
n |
|
Сумма S x ряда (8) есть предельная функция функциональной последовательности его частичных сумм (10).
ряда (8) есть предельная функция функциональной последовательности его частичных сумм (10).
В области D будем применять запись
un x S x . n 1
S x . n 1
Свойства S x зависят, как будет указано ниже, от свойств членов un x
зависят, как будет указано ниже, от свойств членов un x ряда (8) и от характера его сходимости.
ряда (8) и от характера его сходимости.
Пример 7. Рассмотрим функциональный ряд
1 x x 2 |
x n 1 |
x n 1 . |
|
|
n 1 |
Члены этого ряда представляют собой геометрическую прогрессию с первым членом, равным единице, и со знаменателем q x . При всех значени-
ях x , удовлетворяющих условию x 1, соответствующие числовые ряды будут сходиться, а при x 1 – расходиться (см. пункт 2 из [7]). Рекоменду-
ем обратить внимание на числовые ряды, получающиеся из этого ряда при x 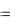 1 и x 1. Таким образом, данный ряд сходится в интервале
1 и x 1. Таким образом, данный ряд сходится в интервале 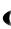 1,1 , а его сумма есть функция (см. формулу (11) из [7])
1,1 , а его сумма есть функция (см. формулу (11) из [7])
1
S x 1 x ,
т.е. в интервале 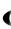 1,1
1,1
1 x x2 |
xn 1 |
|
1 |
|
. |
|
|
|
|||
|
|
|
|||
|
1 |
|
x |
||
Области сходимости функциональных рядов можно находить с помощью предельных признаков Даламбера и Коши (см. [7], теоремы 6 и 8),
применённых к функциональному ряду |
|
un x |
, составленному из моду- |
n |
1 |
|
|
лей членов ряда (8). Поясним это подробнее.
15

Сначала обратимся к предельному признаку Даламбера. Рассмотрим величину
D x |
lim |
|
un 1 x |
|
||
|
|
|
|
|
||
|
|
un x |
|
|
||
|
|
|
||||
|
n |
|
|
|
||
при тех x , для которых имеет смысл подпредельная величина. Для значений x , удовлетворяющих неравенству D x 1, ряд (8) будет абсолютно сходиться. Для значений x , при которых D x
1, ряд (8) будет абсолютно сходиться. Для значений x , при которых D x 1, ряд будет расходиться (общий член ряда не стремится к нулю). Точки x , для которых D x
1, ряд будет расходиться (общий член ряда не стремится к нулю). Точки x , для которых D x 1, подлежат отдельному рассмотрению, так же как и точки, для которых не
1, подлежат отдельному рассмотрению, так же как и точки, для которых не
определена величина |
|
|
un |
1 |
x |
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
un |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Пример |
8. Найдём |
|
область |
|
|
|
сходимости |
|
функционального ряда |
|||||||||||||||||||||||||||||||||
|
xn |
. Так как |
|
un x |
|
|
|
|
|
xn |
|
, |
|
|
то величина |
|
un |
1 |
x |
не определена |
|||||||||||||||||||||||
1 x2n |
|
|
|
1 x2n |
|
|
|
un |
x |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при x 0 . Но при x |
|
|
|
0 ряд состоит из нулей и поэтому он сходится. Так |
|||||||||||||||||||||||||||||||||||||||
как (при x 0) |
|
un 1 x |
|
|
|
|
|
x |
|
n 1 |
|
|
: |
|
|
|
x |
|
n |
|
x |
|
|
|
1 x2n |
|
, то для величи- |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
un |
x |
|
|
|
|
1 |
|
|
|
x2 n 1 |
|
|
1 x2n |
|
1 |
|
|
x2n |
2 |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
ны D x получим следующие ответы:
получим следующие ответы:
|
|
|
|
|
|
|
|
x |
, |
если |
x |
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
D x |
|
1, |
если |
x |
|
|
1; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
, |
|
если |
x |
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Поясним лишь, как получается ответ при |
x |
|
|
|
1 (первые два случая оче- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
|
1 |
|
1 |
|
|||||||
|
|
|
|
|
1 x2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
видны). Действительно, |
|
x |
|
|
|
|
|
x |
|
|
|
x2n |
|
|
x |
|
|
|
|
x2n |
и так |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
2n |
2 |
|
|
1 |
|
|
|
|
2 |
|
|
|
2 |
1 |
|
|
||||||||||||||||
|
|
|
1 |
x |
|
|
|
|
|
|
|
|
x |
|
x |
|
1 |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2n |
|
|
|
|
|
|
|
|
|
|
|
x2n 2 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
16
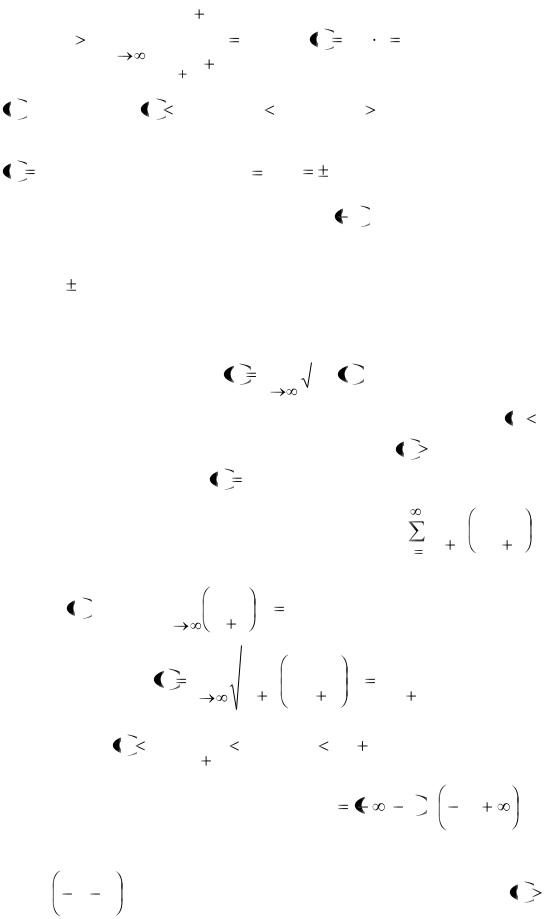
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
как при |
|
x |
|
1 lim |
|
|
x |
2n |
1 |
, |
то D x |
|
|
x |
|
1 |
1 |
|
|
|
. |
Из выражения для |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
1 |
|
|
|
x2 |
|
x |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
n |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
x2n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
D x |
видно, что D x |
|
1 и при |
x |
1 и при |
|
x |
|
1. Следовательно, при та- |
||||||||||||||||||||||
ких x ряд сходится абсолютно. |
Осталось рассмотреть ситуацию, когда |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||
D x |
1. Это происходит при |
x |
|
|
|
1 ( x 1). Но при таких x получаются |
|||||||||||||||||||||||||
числовые ряды соответственно с членами |
1 |
|
n 1 |
и |
1 |
, не стремящиеся к |
|||||||||||||||||||||||||
|
|
|
2 |
2 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
нулю; такие числовые ряды расходятся. Итак, во всех точках числовой оси, кроме x  1, рассматриваемый функциональный ряд абсолютно сходится.
1, рассматриваемый функциональный ряд абсолютно сходится.
Обратимся теперь к предельному (радикальному) признаку Коши. В этом случае находят предел
K x |
lim n |
|
u |
n |
x |
|
, |
|
n |
|
|
|
|
|
|
если он существует. Тогда для тех значений x , при которых K x 1 , ряд
1 , ряд
(8) будет сходиться абсолютно. При тех x , где K x |
|
|
|
1, ряд будет расхо- |
|||||||||||||||||||||||||||||||||||||||
диться. Точки, в которых K x |
|
|
|
1, подлежат отдельному рассмотрению. |
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
x |
|
|
n |
|||
Пример 9. Найдём область сходимости ряда |
|
|
|
|
|
|
. Вы- |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
1 n |
1 |
|
2x 1 |
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
числим K x . Так как lim |
|
|
|
|
|
|
n |
1, то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
n |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K x |
|
|
lim n |
|
|
|
n |
|
|
|
|
x |
|
|
|
n |
|
|
|
|
x |
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
n 1 |
|
|
2x |
1 |
|
|
|
|
2x |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
Неравенство K x 1 ( |
|
|
|
x |
|
|
|
|
1 или |
|
x |
|
|
|
2x |
1 |
|
, которое можно решить |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
2x 1 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
D |
|
|
|
, 1 |
|
1 |
, |
|
|
|
|
||||||||||||||
графически) выполняется на множестве |
|
|
|
|
|
. Следо- |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|||
вательно, на этом множестве исследуемый ряд сходится абсолютно. На ин-
тервале |
1, |
1 |
|
, очевидно, будет выполняться неравенство K x 1. На |
|
3 |
|||||
|
|
|
|||
17
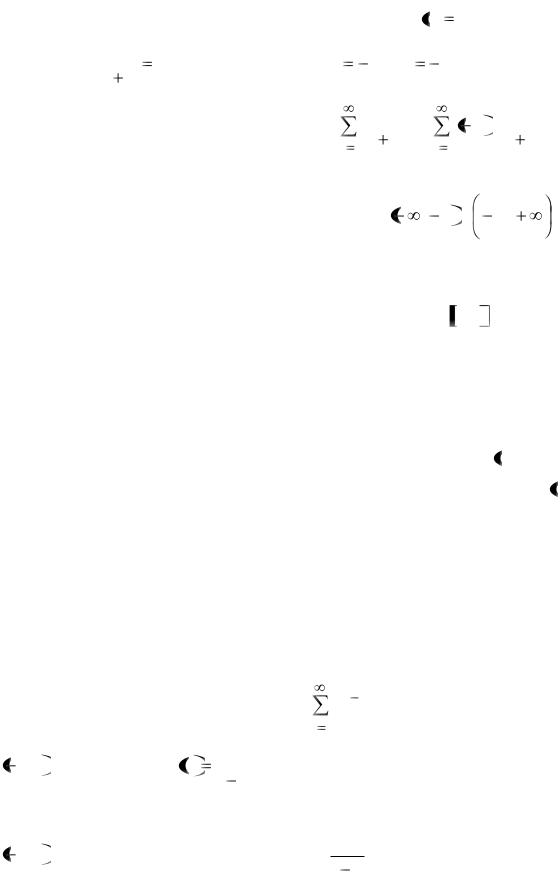
этом интервале ряд будет расходиться. Равенство K x 1 в данном случае
1 в данном случае
имеет вид |
x |
|
|
1 и выполняется при |
x |
|
1 и x |
|
1 |
. При таких x , со- |
|||||||||
|
|
|
|
|
|
||||||||||||||
2x |
1 |
3 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ответственно, получатся числовые ряды |
|
|
n |
и |
|
|
|
1 n |
|
n |
|
|
, общие |
||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||
n |
1 n 1 |
n 1 |
n |
|
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||
члены которых не стремятся к нулю; эти ряды расходятся. Итак, исследуе-
мый функциональный ряд сходится в области |
, 1 |
1 |
, |
, при- |
|
3 |
|||||
|
|
|
|
чём абсолютно.
Читателю хорошо известны свойства суммы конечного числа непрерывных на некотором промежутке (например, отрезке a, b ) функций. Такая сумма будет непрерывной функцией на этом промежутке; её можно почленно проинтегрировать. Если слагаемые будут непрерывно дифференцируемыми, то и сумма будет непрерывно дифференцируемой на соответствующем промежутке.
Так как в области D сходимости ряда (8) его сумма S x есть некоторая функция, то возникает вопрос о функциональных свойствах S x
есть некоторая функция, то возникает вопрос о функциональных свойствах S x как суммы бесконечного числа слагаемых. Для суммы ряда упоминавшиеся свойства конечных сумм могут не сохраниться.
как суммы бесконечного числа слагаемых. Для суммы ряда упоминавшиеся свойства конечных сумм могут не сохраниться.
Поясним пока только случай непрерывности. Некоторые функциональные ряды с непрерывными членами имеют своей суммой непрерывную функцию; у других же рядов (даже с непрерывными членами) сумма может быть функцией с разрывами.
Пример 10. |
Рассмотрим |
ряд |
xn 1 , |
сходящийся на |
интервале |
||||
|
|
|
|
|
|
n 1 |
|
|
|
1,1 к функции |
S x |
1 |
|
(см. |
пример |
7). Все члены |
1, x , x2 , |
||
|
|
|
|||||||
1 x |
|||||||||
|
|
|
|
|
|
||||
x3 , … этого функционального ряда являются непрерывными на интервале
1
1,1 функциями. Предельная функция 1 x (сумма ряда) является также непрерывной функцией на этом интервале.
18

Пример 11. Рассмотрим ряд
x x2 x |
x3 |
x2 |
xn xn 1 |
. |
||||
Так как |
|
|
|
|
|
|
|
|
Sn x x x2 x |
x3 |
x2 |
x4 |
x3 |
xn 1 |
xn 2 |
xn xn 1 xn , |
|
то |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S x |
lim Sn |
x |
0, если |
x |
1; |
|
|
|
1, если x |
1. |
|
|||||
|
|
n |
|
|
|
|||
Это означает, что ряд сходится на полуотрезке 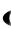 1,1
1,1 к предельной функции S x , которая является разрывной на этом промежутке (разрыв в точке x 1). Очевидно, что члены данного ряда на этом промежутке непрерывны.
к предельной функции S x , которая является разрывной на этом промежутке (разрыв в точке x 1). Очевидно, что члены данного ряда на этом промежутке непрерывны.
Сейчас по аналогии с понятием равномерной сходимости функциональной последовательности будет введено понятие равномерной сходимости функционального ряда, которое и позволит решить вопрос о функциональных свойствах предельной функции S x – суммы функционального ряда.
Определение 5. Функциональный ряд (8) называется равномерно сходящимся на некотором промежутке своей области сходимости D ,
если на этом промежутке равномерно сходится последовательность Sn x его частичных сумм к функции S x
его частичных сумм к функции S x – сумме этого ряда.
– сумме этого ряда.
Замечание 11. На основании определения 2 последнее определение можно сформулировать так: функциональный ряд называется равномерно сходящимся к своей сумме S x на некотором промежутке области сходи-
на некотором промежутке области сходи-
мости этого ряда, если для всякого числа |
|
0 можно выбрать не завися- |
||||
щий от x номер N |
так, что для всех n |
N |
и всех x из данного про- |
|||
межутка будет выполняться неравенство |
|
|
||||
|
|
Sn x |
S x |
|
. |
(14) |
|
|
|
||||
Замечание 12. Последнему определению можно дать несколько дру- |
||||||
гую формулировку с учётом того, |
что разность между суммой ряда S x и |
|||||
его n -й частичной суммой Sn x есть остаток rn x
есть остаток rn x этого функционального ряда (см. (11)). Тогда можно сказать, что ряд (8) равномерно сходится на
этого функционального ряда (см. (11)). Тогда можно сказать, что ряд (8) равномерно сходится на
19

некотором промежутке, если для любого 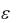 0 можно найти номер N
0 можно найти номер N 
 такой, что для всех n N
такой, что для всех n N 
 и всех x из данного промежутка выполняется неравенство
и всех x из данного промежутка выполняется неравенство
|
rn x |
. |
(15) |
У сходящихся в смысле равенства (13) функциональных рядов оста- |
|||
ток rn x стремится к нулю при n |
(см. (12)). У равномерно же сходя- |
||
щегося ряда оценка малости остатков при больших номерах n , как отмечено в этом замечании (см. (15)), будет одинаковой для всех x из рассматриваемого промежутка. Замечание 12 означает, что у равномерно сходящегося ряда его остаток rn x равномерно стремится к нулю.
равномерно стремится к нулю.
Пример 12. Рассмотрим функциональный ряд
1 |
1 |
1 |
1 |
|||
|
|
|
|
|
|
|
x 1 x 1 x 2 |
|
x 2 x 3 |
|
x n x n 1 |
||
на отрезке 0,1 , на котором определены все его члены. Каждый член этого ряда, начиная со второго, можно представить в виде
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
|
n |
1, 2, ... . |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x |
n |
x |
n |
1 |
|
|
x |
n |
|
|
x |
n |
1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Так как |
|
lim Sn x |
|
0 , то ряд сходится на этом отрезке, причём его сумма |
||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S x |
равна нулю (см. также пример 2). Докажем, что ряд сходится к своей |
|||||||||||||||||||||||||||||||||||
сумме |
равномерно. |
Неравенство |
|
(14) |
|
в |
|
|
этом |
|
случае |
|
имеет вид |
|||||||||||||||||||||||
|
|
0 |
|
. |
|
Так |
как |
0 |
x |
1, то |
|
1 |
|
|
|
1 |
|
|
|
1 |
. Для |
выполнения |
||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
x |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
n |
|
|
x n |
|
n |
|
|
|||||||||
условия |
|
1 |
|
|
1 |
|
|
необходимо, |
чтобы |
n |
|
1 |
. Тогда в качестве номера |
|||||||||||||||||||||||
|
x |
n |
|
|
n |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
N |
|
можно взять, например, целое число N |
1 |
|
|
1 , где |
1 |
есть целая |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
часть числа |
|
. Следовательно, |
N зависит только от |
|
и не зависит от зна- |
|||||||||||||||||||||||||||||||
чения x из |
0,1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
20

Пример 13. Ряд из примера 11 сходится на полуотрезке  1,1
1,1 к своей сумме
к своей сумме
0, при x 1;
S x
1, при x 1
неравномерно, так как последовательность Sn x x его частичных сумм неравномерно сходится к S x
x его частичных сумм неравномерно сходится к S x на этом промежутке (см. пример 5 и замечание 3).
на этом промежутке (см. пример 5 и замечание 3).
Имеются критерии (необходимые и достаточные признаки) равномерной сходимости функциональной последовательности (1) и функционального ряда (8). Сформулируем без доказательства признак равномерной сходимости последовательности функций.
Теорема 4 (критерий равномерной сходимости функциональной
последовательности). Последовательность |
fn x |
действительных функ- |
|||
ций равномерно сходится на некотором промежутке X к своей предель- |
|||||
ной функции f x тогда и только тогда, когда для любого числа |
0 |
||||
найдется такой не зависящий от x номер N |
, |
что при всех n N |
и |
||
любом m 1, 2, 3, ... имеет место неравенство |
|
|
|
||
|
fn m x fn x |
|
|
|
(16) |
|
|
|
|
||
одновременно для всех x из X . |
|
|
|
||
В случае функционального ряда (8) надо в теореме 4 вместо |
fn x |
||||
рассматривать последовательность Sn x его частичных сумм. Тогда неравенство (16) примет вид
его частичных сумм. Тогда неравенство (16) примет вид
|
|
Sn |
m x |
Sn x |
|
|
|
|
или (в силу (10)) |
|
|
|
|
|
|
||
|
un 1 x un |
2 x |
un m x |
|
. |
(17) |
||
|
|
|||||||
Для установления равномерной сходимости конкретных последовательностей или рядов указанные условия мало пригодны, так как надо доказывать справедливость соответствующих неравенств (16), (17) при соответствующих условиях теоремы 4. На практике пользуются основанными на них, но более удобными в применении, теперь уже достаточными признаками равномерной сходимости.
21

Простейшим и чаще всего применяемым достаточным признаком равномерной сходимости функциональных рядов является признак Вейерштрасса, при выполнении условий которого ряд будет ещё и абсолютно сходящимся.
Теорема 5 (признак Вейерштрасса). Пусть члены функционального ряда (8) удовлетворяют на некотором промежутке X неравенствам
|
un x |
|
cn n |
1, 2, 3, ... |
(18) |
и числовой положительный ряд |
|
|
|
||
|
cn c1 |
c2 |
cn |
(19) |
|
n 1 |
|
|
|
||
с членами cn cn 0 сходится. Тогда ряд (8) сходится на X равномерно, причём абсолютно.
сходится. Тогда ряд (8) сходится на X равномерно, причём абсолютно.
Доказательство теоремы проще всего провести на основе критерия (необходимого и достаточного признака) сходимости числового ряда. В [7] (см. теорему 2) приводился критерий сходимости только положительных числовых рядов. Теперь сформулируем критерий, пригодный для любых числовых рядов.
Числовой ряд с членами un сходится тогда и только тогда, когда для
любого |
0 можно указать такой номер N |
|
, что при всех n |
N |
и |
|||
любом m |
1, 2, 3, ... выполняется неравенство |
|
|
|
|
|
||
|
|
un 1 x |
un m x |
|
. |
|
|
(20) |
|
|
|
|
|
||||
Неравенство (20) означает, что суммы un 1 x |
un m x |
ряда для |
||||||
достаточно больших номеров n сколь угодно малы, каково бы ни было в них число m слагаемых (сравните этот критерий с критерием сходимости числовой последовательности; см., например, [4]).
Теперь приступим к доказательству теоремы 5.
Так как по условию теоремы ряд (19) сходится, то из только что сформулированного критерия сходимости числового ряда следует неравенство (см. (20))
cn 1 
 cn m
cn m 
 ,
,
22
которое выполняется при любом m |
1, 2, 3, ... и всех n N |
для любого |
|
0. В силу неотрицательности членов ряда (19) это неравенство примет |
|||
вид |
|
|
|
cn 1 |
cn m |
. |
|
Из этого последнего неравенства, свойства абсолютной величины и неравенств (18) получается неравенство
un 1 x |
un m x |
|
un 1 x |
|
un m x |
cn 1 |
cn m . |
Таким образом, установлено неравенство (17), которое выполняется для
всех x из промежутка X при любом натуральном числе m и любом |
0 , |
начиная с некоторого номера. Этим самым доказана равномерная сходимость функционального ряда (8).
Докажем теперь абсолютную сходимость этого ряда. Так как ряд (19) сходится, то из неравенств (18) и признака сравнения для положительных
рядов (см., например, теорему 3 в [7]) следует сходимость ряда |
|
un x |
n |
1 |
|
при каждом фиксированном x из промежутка X . Тогда по теореме Коши
(см. [7]) сходится ряд un x для каждого x из X . Следовательно, ряд
для каждого x из X . Следовательно, ряд
n1
(8)сходится абсолютно. Теорема доказана.
Определение 6. Функциональный ряд (8) называется мажорируемым на некотором промежутке X , если существует такой положительный сходящийся числовой ряд (19), что при всех x из X выполняются неравенства (18). При этом числовой ряд (19) называют мажорирующим или мажорантным рядом для функционального ряда (8).
Непосредственно из этого определения следует, что теорему 5 можно сформулировать так: мажорируемый на некотором промежутке функциональный ряд сходится на этом промежутке абсолютно и равномерно.
Пример 14. Рассмотрим функциональный ряд
cos x |
|
cos 2x |
|
cos3x |
|
cos nx |
|
cos nx |
. |
|
|
|
|
|
|
|
|
||
1 |
22 |
32 |
|
n2 |
n 1 n2 |
||||
23

Так как на всей координатной прямой Ox при любом натуральном числе n имеем cosnx 1, то справедливы неравенства
cosnx |
|
1 |
, |
|
n2 |
|
|
n2 |
|
|
|
|
||
т.е. данный функциональный ряд мажорируется сходищимся числовым ря-
1
дом n 1 n2 (см. [7]). Следовательно, этот функциональный ряд сходится
абсолютно и равномерно на всей числовой оси.
Замечание 13. Признак Вейерштрасса является достаточным признаком для равномерной сходимости функционального ряда. Поэтому могут быть ряды, не являющиеся мажорируемыми, но равномерно сходящимися на некоторых промежутках.
Пример 15. Функциональный ряд |
|
1 n |
1 |
|
сходится при любом |
||||||||||||||
n 1 x2 |
n |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
x из |
, |
, так как является рядом лейбницевского типа (см. пункт 8 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
1 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
в [7]). |
Для членов этого ряда выполняется условие |
|
un x |
|
|||||||||||||||
|
|
x2 |
n |
|
|
n |
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|||||
n 1, 2, 3, ... , |
однако ряд |
|
, называемый гармоническим, расходится |
||||||||||||||||
|
|
||||||||||||||||||
|
|
n |
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
(см. пункт 2 в [7]). Мажорирующего числового ряда для данного функционального ряда не существует. Но этот ряд является равномерно сходящимся на всём бесконечном промежутке; докажем это.
Известно, что остаток ряда лейбницевского типа оценивается по абсолютной величине модулем своего первого члена (см. формулу (46) из [7]). Тогда в данном случае имеем
|
|
|
|
rn |
x |
|
|
1 |
|
1 |
|
. |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
x2 |
n |
1 |
|
n 1 |
||||
|
|
|
|
|
|
|
|
|
|||||
Очевидно, что существует |
номер |
N |
, |
удовлетворяющий неравенству |
|||||||||
1 |
|
при любом |
0. |
Это значит, |
что для всех x из числовой оси |
||||||||
|
|
|
|||||||||||
|
n 1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
24

справедлива оценка (15) с независящим от x номером N  . Следовательно, рассматриваемый ряд на всей числовой оси сходится равномерно.
. Следовательно, рассматриваемый ряд на всей числовой оси сходится равномерно.
Теперь приступим к решению вопроса, уже поставленного ранее, о функциональных свойствах ряда (8) как бесконечной суммы функций. Хорошо известные свойства суммы конечного числа функций при соответствующих условиях на слагаемые (непрерывность, дифференцируемость, интегрируемость) не всегда переносятся на бесконечные суммы функций. В этом можно убедиться на примерах. Читатель уже видел на примере 11, что сумма функционального ряда, составленного из непрерывных функций, является разрывной функцией. Введённое понятие равномерной сходимости ряда позволяет указать достаточные условия непрерывности его суммы, почленного дифференцирования и почленного интегрирования.
Далее будут приведены без доказательства соответствующие теоремы. За их доказательством можно обратиться к дополнительной литературе.
Теорема 6 (о непрерывности суммы ряда). Если все члены un x
функционального ряда (8) непрерывны на некотором промежутке X и этот ряд равномерно сходится на X к своей сумме S x , то функция S x непрерывна на X .
непрерывна на X .
Эта теорема справедлива для промежутков, которыми могут быть: отрезки, полуотрезки, интервалы, числовые лучи, вся числовая ось.
Пример 16. |
Функция S x |
|
cos nx |
будет непрерывной на всей |
||
n 1 |
n2 |
|||||
|
|
|
||||
числовой оси Ox , |
так как ряд |
cos nx |
состоит из непрерывных функций |
|||
n2 |
||||||
|
n 1 |
|
|
|||
и равномерно сходится на всей координатной прямой (см. пример 14). Замечание 14. Равномерная сходимость ряда является достаточным
условием непрерывности его суммы, но не необходимым. Имеются неравномерно сходящиеся ряды, сумма которых есть непрерывная функция. В
качестве примера можно взять ряд |
xn 1 из примера 10, сходящийся на |
n |
1 |
25
интервале |
1,1 к непрерывной функции S x |
1 |
. Однако он сходится |
|
|
|
|||
1 x |
||||
на этом интервале неравномерно. Докажем это. Рассматриваемый ряд яв-
ляется геометрическим со знаменателем q |
|
x . Тогда согласно формуле (2) |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
xn |
|
|
|
|
|
||||
из [7] его частичная сумма Sn x имеет вид |
|
|
|
|
|
. Остаток ряда выража- |
|||||||||||||||||
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
x |
|
|
|
|
|
||||
ется следующим образом: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
1 xn |
1 |
|
|
|
1 |
|
xn |
|
xn |
|||||||||||
rn x S x Sn x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
1 x 1 x 1 x |
1 x 1 x |
|
|||||||||||||||||||||
|
1 x |
||||||||||||||||||||||
Неравенство (15) в этом случае имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
rn |
x |
|
|
|
xn |
|
|
|
. |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
1 x |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
При каждом конкретном значении n при приближении x к единице чис-
xn
литель дроби 1 x возрастает, стремясь к единице, а знаменатель убывает,
стремясь к нулю. Поэтому вся дробь возрастает по мере приближения x к единице. Неравенства (15) с независящим от x номером N 
 быть не может; по мере приближения x к единице этот номер будет неограниченно возрастать. Следовательно, ряд на
быть не может; по мере приближения x к единице этот номер будет неограниченно возрастать. Следовательно, ряд на  1,1
1,1 не является равномерно сходящимся.
не является равномерно сходящимся.
Если же сумма S x функционального ряда разрывна на некотором промежутке, то этот ряд сходится неравномерно на этом промежутке (см. пример 11). Действительно, если бы ряд сходился равномерно, то по теореме 6 сумма была бы непрерывной.
функционального ряда разрывна на некотором промежутке, то этот ряд сходится неравномерно на этом промежутке (см. пример 11). Действительно, если бы ряд сходился равномерно, то по теореме 6 сумма была бы непрерывной.
Теорема 7. Если члены un x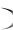 функционального ряда (8) непрерывны на отрезке a, b
функционального ряда (8) непрерывны на отрезке a, b и этот ряд равномерно сходится на этом отрезке к своей сумме S x , то справедливо равенство
и этот ряд равномерно сходится на этом отрезке к своей сумме S x , то справедливо равенство
b |
b |
b |
b |
|
|
S x dx |
un x dx |
u1 x dx |
un x dx |
. |
(21) |
a |
n 1a |
a |
a |
|
|
26

Замечание 15. Поскольку ряд (8) сходится S x |
un x , то ра- |
|
|
n |
1 |
венство (21) можно записать в следующем виде: |
|
|
b |
b |
|
un x dx dx |
un x dx . |
|
a n 1 |
n 1 a |
|
Последнее означает, что интеграл от суммы ряда равен сумме ряда, составленного из интегралов его членов. Тогда теорему 7 можно сформулировать так: в случае равномерно сходящегося ряда, составленного из не-
прерывных функций, допустимо почленное интегрирование ряда.
Замечание 16. Теорема 7 обобщается в том смысле, что требование
непрерывности членов un x |
ряда заменяется требованием их интегрируе- |
||||||||||||||||||
мости на отрезке |
a, b . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 17. Снова рассмотрим ряд |
|
|
xn 1 из примера 10, сходя- |
||||||||||||||||
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
щийся на интервале |
1,1 |
к непрерывной функции |
S x |
|
1 |
|
. На про- |
||||||||||||
|
|
|
|
||||||||||||||||
|
1 |
x |
|||||||||||||||||
межутке 0, t , где t |
1, ряд будет равномерно сходящимся. Согласно тео- |
||||||||||||||||||
реме 7 его можно интегрировать по промежутку |
0, t |
. В |
результате |
||||||||||||||||
почленного интегрирования получится ряд |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
t |
t |
|
t |
n |
1 |
|
|
1 |
|
2 |
1 |
|
n |
|
|
||||
|
|
|
|
|
|
|
|
|
|
||||||||||
1 dx |
xdx |
|
x |
|
|
dx |
t |
|
|
t |
|
|
|
t |
|
|
. |
||
|
|
|
2 |
|
|
n |
|
|
|||||||||||
0 |
0 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
С другой стороны, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
t |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 S x dx |
|
|
dx |
ln 1 t . |
|
|
|
|
|
|
|
||||||
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||
|
|
|
1 x |
|
|
|
|
|
|
|
|||||||||
В силу равенства (21) получим следующее представление логарифмиче-
ской функции на полуотрезке |
0,1 : |
|
|
|
|
|
ln 1 x |
x |
x2 |
|
x3 |
|
xn |
2 |
3 |
|
n |
|||
|
|
|
||||
(переменную t заменили на x ).
27
Замечание 17. В теореме 7 условие равномерной сходимости ряда на a, b представляет собой достаточное условие для его почленного интегрирования, но необходимым условием не является. Для некоторых неравномерно сходящихся рядов их почленное интегрирование допустимо.
представляет собой достаточное условие для его почленного интегрирования, но необходимым условием не является. Для некоторых неравномерно сходящихся рядов их почленное интегрирование допустимо.
Теорема 8. Пусть члены un x сходящегося на отрезке a, b
сходящегося на отрезке a, b функционального ряда (8) имеют на этом отрезке непрерывные производные un x
функционального ряда (8) имеют на этом отрезке непрерывные производные un x и составленный из этих производных функциональный ряд
и составленный из этих производных функциональный ряд
u1 x |
u2 x |
un x |
un x |
(22) |
|
|
n |
1 |
|
равномерно сходится на |
a, b . Тогда сумма S x |
ряда (8) имеет на |
a, b |
|
производную, причем справедливо равенство |
|
|
||
|
S x |
un x . |
|
(23) |
|
|
n 1 |
|
|
d
Замечание 18. Воспользовавшись обозначением для производ- dx
ной, равенство (23) можно переписать в виде
d |
un x |
|
d |
un x . |
|
dx |
n 1 dx |
||||
n 1 |
|
||||
Эту запись можно сформулировать следующим образом: производная от суммы ряда равна сумме ряда, составленного из производных его членов. Таким образом, при указанных в теореме 8 условиях допустимо почленное дифференцирование ряда. Часто теорему 8 кратко формулируют так: сходящийся ряд можно почленно дифференцировать, если после дифференцирования получится равномерно сходящийся ряд.
Пример 18. Выясним, возможно ли почленное дифференцирование
ряда |
|
sin nx |
. Так как на |
, |
|
справедливо неравенство |
|||
1 n3 |
|
||||||||
n |
|
|
|
|
|
|
|
||
|
|
|
|
sin nx |
|
|
1 |
n 1, 2, 3, ... |
, |
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
||
|
|
|
|
n3 |
|
|
n3 |
||
|
|
|
|
|
|
|
|
||
28
