
5628
.pdfМинистерство образования и науки Российской Федерации Государственное бюджетное образовательное учреждение высшего профессионального образования
"Хабаровская государственная академия экономики и права" Кафедра математики и математических методов в экономике
Математика
Практикум для студентов 1 и 2 курсов очной и заочной форм обучения
по направлению 230700 "Прикладная информатика"
2014
1
Математика . Практикум для студентов 1 и 2 курсов очной и заочной форм
обучения |
по направлению |
230700 "Прикладная информатика /сост. Е. Н. |
Кравченко, С.А. Наумова – Хабаровск : ХГАЭП, 2014. – 62 с.
Рецензент Е.В. Карачанская, кандидат физ.- мат. наук доцент каф. прикладной математики ТОГУ.
Утверждено УМУ академии в качестве методического пособия для студентов очной и заочной форм обучения.
Елена Николаевна Кравченко
Светлана Александровна Наумова Математика
Практикум для студентов 1 и 2 курсов очной и заочной форм обучения по направлению 230700 «Прикладная информатика»
680042, г. Хабаровск, ул. Тихоокеанская, 134, ХГАЭП
©Е. Н. Кравченко, С.А. Наумова 2014
©Хабаровская государственная академия экономики и права, 2014
2
ПРЕДИСЛОВИЕ
Математика играет важную роль в естественнонаучных, инженернотехнических и гуманитарных исследованиях. Математическое образование следует рассматривать как важнейшую составляющую в системе фундаментальной подготовки специалистов в области информатики.
Настоящий практикум по теории вероятностей и математической статистики представляет собой учебное пособие для студентов 1 и 2 курсов очной и заочной форм обучения по направлению 230700 "Прикладная информатика" .
Данная разработка содержит основные вопросы курса.
Чтобы обеспечить студентам усвоение материала, рассмотрены некоторые основные сведения из теории, приведены примеры решения типовых задач. В практикум включены примерные варианты аудиторных контрольных и тестовых
работ, задания по каждой теме для самостоятельного выполнения. |
|
Пособие позволит приобрести навыки самостоятельного |
использования |
теоретических знаний на практике. |
|
3
Программа дисциплины Раздел 1. Элементы аналитической геометрии
1.1. Система координат на плоскости, основные понятия
Числовая ось. Декартовая прямоугольная система координат на плоскости. Расстояние между двумя точками. Деление отрезка в данном отношении.
1.2. Линия на плоскости. Прямая
Общее уравнение прямой и его исследование. Уравнение прямой с угловым коэффициентом. Уравнение прямой, проходящей через две точки. Уравнение прямой в отрезках. Угол между двумя прямыми. Условия параллельности и перпендикулярности двух прямых. Уравнение пучка прямых. Расстояние от точки до прямой. Нормальное уравнение прямой. Геометрический смысл неравенства и системы неравенств первой степени с двумя неизвестными.
1.3 . Кривые второго порядка
Окружность. Эллипс. Гипербола. Парабола. Дробно-линейная функция.
Раздел 2. Элементы линейной алгебры
2.1. Матрицы
Матрица, её размерность. Виды матриц: диагональная, симметрическая, единичная. Операции над матрицами: сложение матриц, умножение матрицы на число, умножение матриц, транспонирование матриц. Свойства операций над матрицами.
2.2. Определители матриц
Определители квадратных матриц различных порядков. Свойства определителей. Миноры и алгебраические дополнения. Алгоритм Гаусса, вычисления определителя п-го порядка. Разложение определителя по элементам строки (столбца).
2.3.. Системы линейных алгебраических уравнений
Система линейных алгебраических уравнений и её решение. Системы однородные и неоднородные, совместные и несовместные, определённые и неопределённые. Эквивалентные системы. Системы с базисом, канонические системы. Методы решения систем уравнений. Метод Крамера. Обратная матрица. Матричный метод. Метод Жордана – Гаусса.
Раздел 3. Элементы векторной алгебры
3.1. Векторы. Векторная алгебра
Векторы в R2 и R3. Действия над векторами: сложение векторов, умножение на число, скалярное произведение векторов. Длина вектора. Угол между векторами.
3.2. Векторное пространство Rn
4
N-мерный арифметический вектор. Размерность и базис векторного пространства. Линейная зависимость векторов. Переход к новому базису.
Раздел 4. Функции одной переменной
4.1. Числовые множества
Понятие множества. Операции над множествами.
4.2. Функция одной переменной
Определение функции одной переменной. Способы задания. Монотонные функции. Ограниченные и неограниченные функции. Чётные и нечётные функции. Сложная функция. Обратная функция. Основные элементарные функции(область определения, график, характеристики поведения). Примеры поведения элементарных функций в экономике (функция спроса, предложения, издержек и т.д.)
Раздел 5. Теория пределов
5.1. Предел числовой последовательности
Числовая последовательность (определение, обозначение, способы задания). Предел числовой последовательности. Геометрическая интерпретация предела. Теоремы об единственности предела, об ограниченности сходящейся
последовательности. |
Бесконечно малые |
и бесконечно большие |
величины |
|
(последовательности), |
связь между ними. |
Свойства |
бесконечно |
малых |
последовательностей. Связь сходящихся последовательностей с бесконечно малым (второе определение предела последовательности). Арифметические операции над последовательностями. Предельный переход в равенствах и неравенствах. Достаточное условие сходимости монотонной последовательности.
5.2. Предел функции |
|
Предел функции (на языке последовательности). |
Раскрытие |
неопределённостей различных видов. Первый и второй замечательные пределы. Эквивалентные бесконечно малые.
Раздел 6. Непрерывные функции
Односторонние пределы. Непрерывность функции в точке. Точки разрыва функции и их классификация. Свойства функций непрерывных на отрезке. Приращение функции. Второе определение непрерывности функции в точке.
5
Раздел 7. Дифференциальные исчисления
7.1 Производная функции одной переменной
Задачи, приводящие к понятию производной. Определение производной. Уравнение касательной. Производная как показатель мгновенного прироста или скорости изменения функции. Простейшие предельные характеристики из экономического анализа (предельная выручка, предельный доход, предельные издержки, предельная прибыль...) Эластичность функции и её свойства.
Непрерывность дифференцируемой функции. Правила дифференцирования. Производные основных элементарных функций. Производная обратной функции. Производная сложной функции. Логарифмическое дифференцирование. Производные высших порядков.
7.2. Дифференциал функции одной переменной
Дифференциал функций, его геометрический смысл. Инвариантность формы дифференциала. Применение дифференциала в приближенных вычислениях.
Раздел 8 . Теоремы дифференциального вычисления. Исследование функций и построение графиков
8.1. Основные теоремы дифференциального исчисления
Теоремы Ферма, Ролля, Лагранжа. Правило Лопиталя. Признак постоянства функции. Необходимое и достаточное условие монотонности.
8.2. Экстремум функции одной переменной
Экстремум функции одной переменной. Достаточные условия монотонности (первое и второе). Наибольшее и наименьшее значение функции. Задачи на экстремум с экономическим содержанием.
Выпуклость, вогнутость функции y=f(x). Точки перегиба. Асимптоты функции. Схема исследования функции.
Раздел 9. Функции нескольких переменных
9.1. Функции нескольких переменных
Функции нескольких переменных (основные определения). Функция двух переменных. График функции двух переменных. Линии уровня. Предел и непрерывность функции двух переменных. Частные приращения. Частные производные. Полное приращение. Полный дифференциал. Частные производные высших порядков.
9.2. Экстремум функции двух переменных
Экстремум функции двух переменных. Необходимое условие экстремума. Достаточные условия экстремума. Условный экстремум. Метод наименьших квадратов. Производная по направлению. Градиент функции. Понятие о градиентных методах в задачах оптимизации.
6
Раздел 10. Неопределённый интеграл
Первообразная и её свойства. Неопределённый интеграл и его свойства. Таблица интегралов. Непосредственное интегрирование. Замена переменной, интегрирование по частям. Интегрирование иррациональных функций. Интегрирование рациональных дробей, интегрирование тригонометрических функций. Понятие о неберущихся интегралах.
Раздел 11. Определённый интеграл
Понятие определённого интеграла, его геометрический смысл. Свойства определённого интеграла. Определённый интеграл как функция верхнего предела. Формула Ньютона – Лейбница. Замена переменной и формула интегрирования по частям в определённом интеграле. Геометрические приложения определённого интеграла. Несобственные интегралы с бесконечными пределами интегрирования. Интеграл Пуассона. Несобственные интегралы от неограниченных функций.
Приближённое вычисление определённых интегралов.
Экономический смысл определённого интеграла. Использование определённого интеграла в экономике.
Раздел 12. Ряды
Числовой ряд. Сходимость ряда. Геометрический ряд. Свойства числовых рядов. Необходимый признак сходимости. Сравнение рядов с положительными членами. Признак Даламбера. Интегральный признак. Обобщенно-гармонический ряд. Знакопеременные ряды. Абсолютная и условная сходимость. Знакочередующиеся ряды. Признак Лейбница.
Степенной ряд. Теорема Абеля. Область сходимости степенного ряда.
Раздел 13. Дифференциальные уравнения
Дифференциальные уравнения (определение; порядок; общее решение; частное решение). Дифференциальные уравнения первого порядка; уравнения с разделяющимися переменными; однородные уравнения; линейные уравнения. Математические модели экономического роста.
Линейные дифференциальные уравнения высших порядков. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами (однородные и неоднородные).
7

Тема 1. Элементы аналитической геометрии Прямая линия на плоскости
Каждая прямая на плоскости Oxy определяется линейным уравнением первой степени с двумя неизвестными.
Уравнение прямой с угловым коэффициентом имеет вид
|
|
|
|
|
|
|
|
|
|
|
|
|
y kx |
b , |
|
(1.1) |
|||
где |
k |
tg |
|
– угловой коэффициент прямой, |
угол, между прямой и |
||||||||||||||
положительным направлением оси |
Ox |
|
|
||||||||||||||||
|
|
Уравнение прямой, проходящей через две точки M1 (x1 y1 ) и M 2 (x2 y 2 ) , имеет вид |
|||||||||||||||||
|
х |
х1 |
|
|
у |
у1 |
. |
|
|
|
|
|
|
|
|
(1.2) |
|||
|
х |
|
х |
|
|
у |
|
|
|
|
|
|
|
|
|
|
|||
|
2 |
|
|
2 |
у |
1 |
|
|
|
|
|
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Если x1 |
|
x2 , то уравнение прямой (1.1) имеет вид x |
x1 ; |
||||||||||||||
|
|
если y1 |
|
y2 , то y |
y1 . |
|
|
|
|
|
|
|
|||||||
|
|
Уравнение прямой, проходящей через данную |
точку x0 ; y0 в заданном |
||||||||||||||||
направлении |
y |
y0 |
k(x |
|
x0 ) . |
|
|
(1.3) |
|||||||||||
|
|
Две |
прямые l1 |
и |
l2 заданные |
уравнениями с |
угловыми коэффициентами |
||||||||||||
|
y k1x b1 |
и y k2 x b2 |
|
|
|
|
|
|
|
||||||||||
|
|
параллельны, если |
k1 |
k2 , |
|
|
(1.4) |
||||||||||||
|
|
перпендикулярны, если |
k1 |
1 |
|
или k1 k2 |
1 . . |
(1.5) |
|||||||||||
|
|
|
|
|
|||||||||||||||
|
|
|
k2 |
||||||||||||||||
Пример 1.
Даны вершины треугольника ABC , (рисунок 1). Найти:
1)уравнение стороны AB;
2)уравнение высоты CD, проведённой из вершины C к стороне AB;
3)уравнение медианы BM, проведённой из вершины B к стороне AC.
Решение:
8
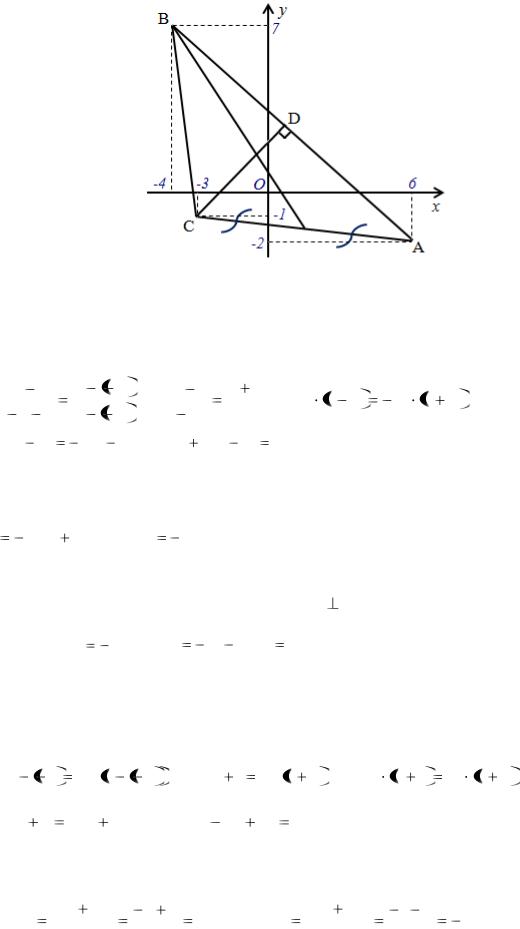
Рисунок 1 ─ Треугольник ABC
1) Для нахождения уравнения стороны AB воспользуемся уравнением прямой, проходящей через две данные точки (1.2). Подставим в эту формулу координаты точек А и В, получим уравнение прямой АВ:
|
х 6 |
|
|
|
у |
2 |
; |
|
х 6 у 2 |
; |
9 х 6 |
10 у 2 ; |
|
|||||||||
|
4 |
6 |
|
|
7 |
|
2 |
|
|
|
10 |
|
9 |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
9х |
54 |
|
|
10у |
20; |
9x |
10y |
34 |
0 |
(АВ). |
|
|
||||||||||
2) |
Высота CD перпендикулярна стороне треугольника AB. Найдём угловой |
|||||||||||||||||||||
коэффициент прямой |
АВ, |
разрешим полученное уравнение относительно y : |
||||||||||||||||||||
y |
|
9 |
x |
|
34 |
; |
k AB |
|
|
|
9 |
. |
|
|
|
|
|
|||||
10 |
10 |
10 |
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Чтобы |
|
|
найти |
уравнение |
высоты |
CD, |
воспользуемся |
условием |
||||||||||||||
перпендикулярности двух прямых (1.5), т.к. CD AB, то угловой коэффициент kCD
будет равен k |
|
1 |
, k |
|
1/( 9 /10) |
|
10 |
. |
|
CD |
kАВ |
CD |
9 |
||||||
|
|
|
|
||||||
|
|
|
|
|
|
||||
Искомая высота проходит через точку С(–3; –1). Воспользуемся уравнением прямой, проходящей через данную точку, с заданным угловым коэффициентом
(1.3) :
y |
1 |
10 |
x |
3 ; |
y 1 |
10 |
x 3 ; |
9 y 1 10 x 3 ; |
|||
|
9 |
|
9 |
||||||||
|
|
|
|
|
|
|
|||||
9 y 9 10x 30 ; |
|
10x 9 y 21 0 (СD). |
|
||||||||
3) По определению медиана BM делит точкой М противолежащую сторону СA пополам. Найдём координаты точки М :
xM |
xC x А |
|
3 6 3 |
; |
yM |
yC y А |
1 2 |
3 |
. |
|||||
2 |
|
2 |
|
2 |
2 |
|
2 |
|
2 |
|||||
|
|
|
|
|||||||||||
Чтобы записать уравнение медианы ВM, воспользуемся формулой (1.2).
9

|
x ( 4) |
y 7 |
|
|
; |
x 4 |
y 7 |
; |
|
17 |
|
x 4 |
11 |
y |
7 ; |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
3/ 2 |
( |
4) |
|
3/ 2 |
7 |
|
11/ 2 |
|
|
|
17 / 2 |
|
|
2 |
|
2 |
||||||||||
17 |
x |
4 |
11 y |
7 |
; |
17x 68 |
11y |
|
77 ; |
|
17x |
11y |
9 |
0 |
(ВМ). |
|||||||||||
Кривые второго порядка |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Эллипс |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Каноническое уравнение эллипса |
(х |
)2 |
|
|
|
( у |
)2 |
|
|
1, |
|
|
|
(1.6) |
||||||||||||
|
а2 |
|
b2 |
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
центр эллипса лежит в точке O/(α,β), a – большая полуось, b – малая полуось эллипса.
Пример 2.
Уравнение кривой привести к каноническому виду и построить линию
4x 2 |
25 y 2 |
16 x |
200 y |
316 |
0. |
|
|
|
||
Решение: |
Выделим полные квадраты при x и y |
|||||||||
4 x 2 |
4x |
22 |
22 |
25 y 2 |
8 y |
42 |
42 |
316 |
0; |
|
4 x 2 |
4x |
22 |
4 |
22 |
25 y 2 |
8 y |
42 |
25 42 |
316 0; |
|
4 x 2
4 x 2
2 |
16 |
25 y |
4 2 400 316 0; |
4 x 2 2 25 y 4 2 100 0; |
2 |
25 y |
4 2 |
100 . |
|
Разделим уравнение на 100 .
|
4 x 2 2 |
|
25 y 4 2 |
x 2 2 |
|
y 4 2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
1; |
|
|
|
|
|
|
|
|
1. |
|
|
|
|
|
|
100 |
100 |
|
25 |
|
4 |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
Получили каноническое уравнение эллипса |
(1.6), |
точка |
O 2; |
4 центр |
|||||||||||||||
данного эллипса, полуоси a |
|
|
5 , b |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
4 |
2. |
|
|
|
|
|
|
||||||||||
25 |
|
|
|
|
|
|
|
|||||||||||||
|
Для построения кривой, |
в системе координат Oxy построим точку |
O 2; |
4 и |
||||||||||||||||
проведём оси параллельно осям координат. Отложим от |
точки O отрезки a |
5 |
, |
|||||||||||||||||
b |
2 в |
направлениях, параллельных Ox |
|
и |
Oy , |
оси эллипса |
CA 2a |
2 5 |
10 |
, |
||||||||||
BD |
2b |
2 2 4 . В получившийся прямоугольник впишем эллипс (рисунок 2). |
|
|||||||||||||||||
Рисунок 2 ─ График функции 4x 2 25y 2 16x 200 y 316 0
10
