
5628
.pdf
Гипербола
Каноническое уравнение гиперболы с осями, параллельными координатным осям, имеет вид (1.7) или (1.8).
|
|
|
(х |
) 2 |
|
|
( у |
) 2 |
1, |
(1.7) |
||||
|
|
|
|
а 2 |
|
b 2 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
(х |
) 2 |
|
|
( у |
|
) 2 |
1, |
(1.8) |
||
|
|
|
|
|
а 2 |
|
b 2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|||||
где |
; |
– координаты центра |
гиперболы, |
|
a – действительная |
полуось, b – |
||||||||
мнимая полуось гиперболы. |
|
|
|
|
|
|
|
|
|
|
||||
Пример 3.
Уравнение кривой привести к каноническому виду и построить линию.
25 x 2 9 y 2 50 x 54 y 281 0.
Решение: Выделим полные квадраты при x и y :
|
25x 2 50x |
9y 2 54 y |
281 |
|
0; 25 x 2 |
2x |
9 y 2 |
6y |
281 |
0; |
|
|
|
|||||||||||||||
25 x 2 |
2x |
1 |
1 |
9 y 2 |
6 y |
32 32 |
281 |
0; |
25 x |
1 2 |
9 y |
3 2 |
225 . |
|
|
|
||||||||||||
Разделим обе части уравнения на 225 , чтобы получить 1 в правой части . |
|
|
|
|||||||||||||||||||||||||
|
25 x 1 2 |
|
9 y 3 |
2 |
1; |
|
|
x 1 2 |
|
|
|
y 3 |
2 |
1. |
|
|
|
|
|
|
|
|||||||
|
225 |
|
|
|
225 |
|
|
|
9 |
|
|
|
|
25 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Получили каноническое уравнение гиперболы (1.7) с центром в точке |
O |
1; 3 |
|||||||||||||||||||||||||
, и полуосями a |
|
|
3 , b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
9 |
|
25 |
|
|
5. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
В системе координат |
Oxy |
|
построим точку |
O |
1; 3 |
и проведём оси O x |
и |
|||||||||||||||||||
O y параллельно осям координат. |
|
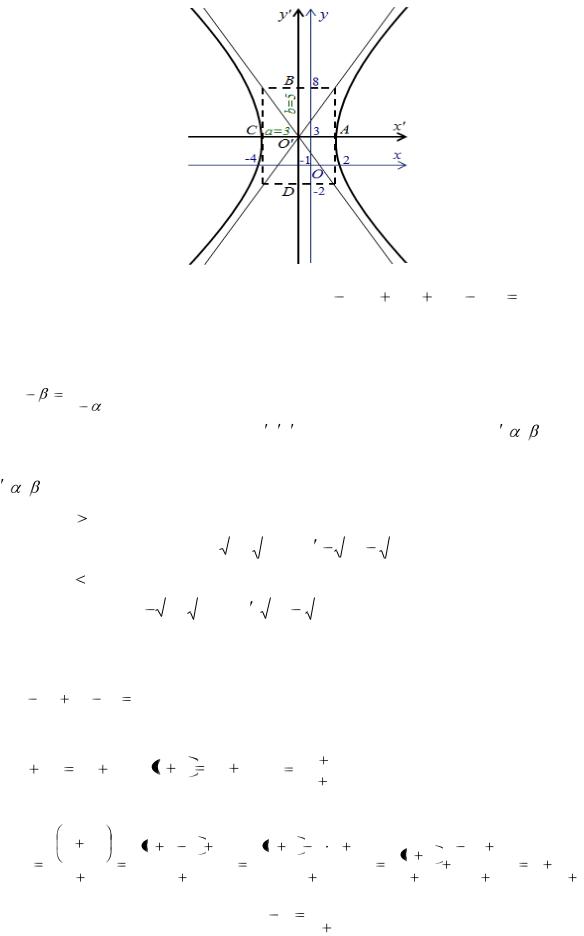
Построим основной прямоугольник гиперболы |
||||||||||||||||||||||||||
в системе координат |
O x y , |
откладывая |
от |
точки O |
отрезки a |
3, |
b |
5 , |
||||||||||||||||||||
CA |
2a |
2 3 |
6 , BD |
2b |
2 5 |
|
10. Диагонали прямоугольника будут являться |
|||||||||||||||||||||
асимптотами гиперболы. Вершины гиперболы – точки A и C |
(рисунок 3). |
|
||||||||||||||||||||||||||
11
|
|
Рисунок 3 ─ График функции 25x 2 |
|
9y 2 |
50x |
54 y 281 0 |
|
|||||||||||||||||||||
Дробно-линейная функция |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Каноническое уравнение |
дробно-линейной функции |
|
|
|
||||||||||||||||||||||||
y |
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1. 10) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
в |
новой |
системе |
координат |
O x y , с |
началом в |
точке O ( , ) задаёт |
||||||||||||||||||||||
равностороннюю |
гиперболу, |
асимптотами которой являются оси |
координат. |
|||||||||||||||||||||||||
O ( , |
) |
─ центр гиперболы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Если |
m |
0 , |
то |
ветви |
гиперболы |
расположены в |
чётных |
квадрантах, |
а |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
вершинами являются точки А( |
|
m; |
|
m) и A ( |
|
m; |
m) . |
|
|
|
||||||||||||||||||
Если |
m |
0 , |
то ветви |
гиперболы |
расположены |
в |
нечётных |
квадрантах, |
а |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
вершины ─ точки |
B( |
|
m; |
m) и B ( m; |
|
m) . |
|
|
|
|
|
|||||||||||||||||
Пример 4.
Уравнение кривой привести к каноническому виду и построить линию. xy 4x 3y 17 0.
Решение: Приведём уравнение к каноническому виду.
xy |
3y 4x |
17; y x 3 |
4x 17; |
y |
4x |
17 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Приведём полученное уравнение к виду (1.10). Выделим целую часть: |
|
|
|
||||||||||||||||||||||||||||
|
|
4 x |
17 |
|
|
4 x 3 3 |
17 |
|
|
4 x 3 4 3 |
17 |
|
|
|
12 |
17 |
|
|
|
|
|||||||||||
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
4 x 3 |
|
|
|
|
5 |
|
|||||||||||
y |
|
|
4 |
4 |
|
|
4 |
|
4 |
; |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x 3 |
|
|
x 3 |
|
|
|
|
|
|
x 3 |
|
|
|
|
|
|
|
x 3 |
|
x 3 |
x 3 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y |
4 |
5 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
12
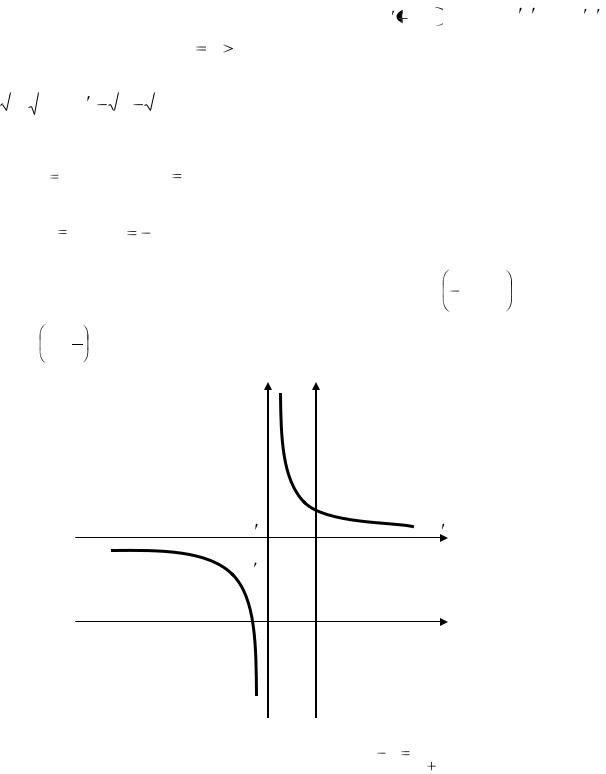
Это уравнение |
гиперболы с |
центром в точке O 3; 4 , |
оси О х и О у |
|||||||||||||||
являются асимптотами, |
m |
5 |
0 ветви гиперболы расположены во втором |
и |
||||||||||||||
четвертом квадрантах, вершинами в новой системе координат |
являются точки |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
A( 5; 5) и A ( |
5; |
|
5) (рисунок 4). |
|
|
|
|
|||||||||||
Найдём точки пересечения функции с осями Ox и Oy . |
|
|
|
|
||||||||||||||
При x |
0 , получаем y |
5 |
2 |
. |
|
|
|
|
|
|||||||||
3 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Если y |
0 , то x |
4 |
1 |
. |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|||
|
Следовательно, |
гипербола пересекает ось Ox в точке С |
4 |
1 |
; 0 и ось Oy |
в |
||||||||||||
|
4 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
точке B 0; 5 23 .
y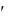 y
y
|
В |
A |
|
O |
x |
|
4 |
A |
|
О |
x |
С-3
Рисунок 4 ─ График функции |
y 4 |
5 |
|
|
|
|
|||
x 3. |
||||
|
|
|||
13

Тема 2. Элементы линейной алгебры Системы линейных уравнений
Дана система трёх линейных уравнений с тремя неизвестными.
a11 x1 |
|
a12 x2 |
a13 x3 |
b1 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
a21 x1 |
|
a22 x2 |
a23 x3 |
b2 ; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(2.1) |
|
||||||||
a31 x1 |
|
a32 x2 |
a33 x3 |
b3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Матричный метод решения систем линейных уравнений |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
Систему уравнений (2.1) можно представить в матричном виде |
A X |
B, где |
|||||||||||||||||||||||||||||
A − основная матрица системы, |
состоящая из коэффициентов уравнений при |
|||||||||||||||||||||||||||||||
неизвестных; |
X − матрица-столбец неизвестных |
|
x1 , x2 , x3 ; |
B |
− матрица-столбец |
|||||||||||||||||||||||||||
свободных членов системы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
Исходную систему уравнений (2.1) можно представить в матричном виде |
A X |
|
B, |
||||||||||||||||||||||||||||
где A |
|
− основная матрица системы, состоящая из коэффициентов уравнений при |
||||||||||||||||||||||||||||||
неизвестных, |
причём |
матрица |
|
A |
квадратная (содержит одинаковое |
число |
строк |
|
и |
|||||||||||||||||||||||
столбцов); |
X − матрица-столбец неизвестных x1 , x2 , x3 ; B − матрица-столбец свободных |
|||||||||||||||||||||||||||||||
членов системы: |
|
|
a11 |
a12 |
a13 |
|
|
x1 |
|
|
b1 |
|
|
|
|
|
|
|
|
|
||||||||||||
A a21 |
a22 |
a23 , |
|
X |
x2 , B b2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
a31 |
a32 |
a33 |
|
|
x3 |
|
|
b3 . |
|
|
|
|
|
|
|
|
||||||
Если матрица |
A невырожденная, |
т.е. определитель матрицы |
отличен от нуля |
|||||||||||||||||||||||||||||
|
A |
|
0 , то исходная система уравнений имеет единственное решение, |
которое |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
находится по формуле |
|
X |
|
A 1 |
B , |
|
|
|
|
|
|
|
|
|
|
|
(2.2) |
|||||||||||||||
где A 1 − обратная матрица к матрице A . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
Определитель третьего порядка матрицы A вычисляется по формуле |
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
a11 |
a12 |
|
a13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
A |
|
|
a21 |
a22 |
|
a23 |
|
a11 |
a22 |
a33 |
a21 |
a32 |
a13 |
a12 |
a23 a31 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
a31 |
a32 |
|
a33 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
a31 |
a22 |
a13 |
a32 a23 |
a11 |
a21 |
a12 |
a33 . |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
A11 |
A21 |
A31 |
|
|
|
|
|||
Обратная матрица находится по формуле A 1 |
|
A |
A |
|
A . |
(2.3) |
|
|||||||||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A |
|
12 |
22 |
32 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A13 |
A23 |
A33 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Алгебраические |
дополнения |
Aij |
элементов aij |
матрицы A находятся по |
||||||||||||||||||||||||||||
формуле |
A |
|
|
1 i |
j M |
ij |
, |
где |
|
M |
ij |
– |
минор |
|
элемента |
a |
ij |
матрицы |
A , |
|||||||||||||
|
|
|
|
|
ij |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
представляющий |
|
собой |
определитель, полученный из основного |
|
|
A |
|
|||||||||||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||
вычёркиванием i - й строки и j - го столбца. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
14
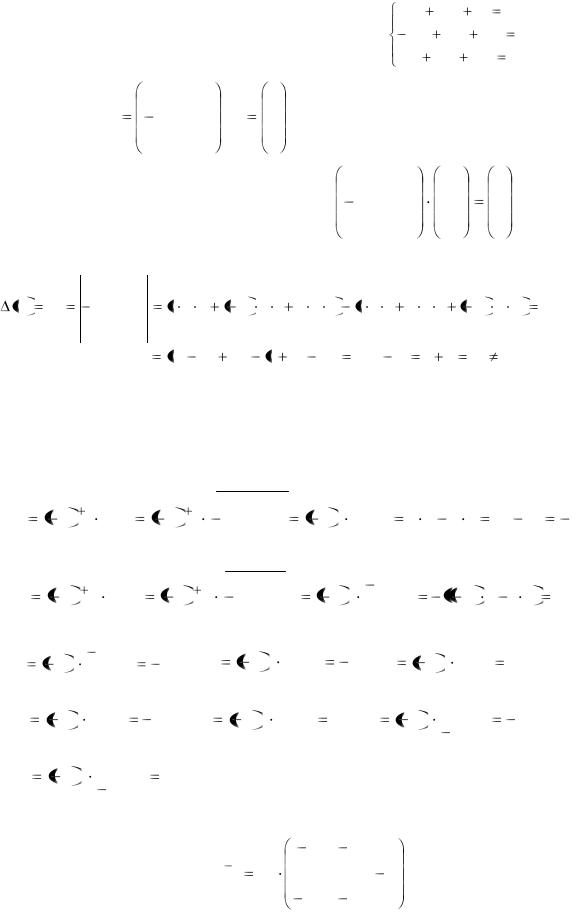
Пример 5 .
|
|
|
|
|
x1 |
4x2 |
x3 |
7; |
Решить систему уравнений матричным методом 4x1 |
8x2 |
3x3 |
9; |
|||||
|
|
|
|
|
x1 |
6x2 |
2x3 |
8. |
|
1 |
4 |
1 |
|
7 |
|
|
|
Решение: A |
4 |
8 |
3 |
, B |
9 . |
|
|
|
|
1 |
6 |
2 |
|
8 |
|
|
|
1 |
4 |
1 |
x1 |
7 |
Матричный вид данной системы уравнений: 4 |
8 |
3 |
x2 |
9 . |
1 |
6 |
2 |
x3 |
8 |
Вычислим определитель матрицы А.
|
|
1 |
4 |
1 |
|
|
|
|
|
|
|
|
|
||
A |
A |
4 8 |
3 |
1 8 2 |
4 6 1 4 3 1 1 8 1 6 3 1 |
4 4 2 |
|
|
|
1 |
6 |
2 |
|
|
|
16 24 12 8 18 32
8 18 32 4
4 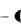 6
6 4 6 10 0.
4 6 10 0.
Т.к. определитель матрицы А не равен 0, то матрица А невырожденная, для неё существует обратная матрица A-1.
Вычислим алгебраические дополнения Aij для каждого элемента aij
основной матрицы.
|
|
1 1 |
|
|
|
|
|
|
|
1 1 |
|
1 |
|
4 |
|
|
1 |
|
|
|
|
|
|
2 |
|
8 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
1 |
|
M |
|
|
1 |
|
|
|
4 8 3 |
|
|
|
|
|
1 |
|
|
8 2 6 3 16 18 |
2; |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
11 |
|
|
|
|
|
|
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
6 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 1 2 |
|
|
|
|
1 1 2 |
|
1 |
|
|
4 |
|
1 |
|
|
|
1 3 |
|
4 |
|
3 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
A |
|
M |
|
|
4 |
8 |
3 |
|
|
|
|
|
|
|
|
4 |
2 |
1 3 |
11; |
|||||||||||||||||||||||||
|
12 |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
6 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
4 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|||||||||||
A |
1 4 |
|
|
|
|
32; |
A |
|
|
|
1 3 |
|
|
4 |
|
|
2; A |
|
|
1 4 |
|
|
1; |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
13 |
|
|
1 |
6 |
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
6 |
2 |
|
|
|
|
22 |
|
|
|
|
|
1 |
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
A |
1 |
5 |
|
|
|
4 |
|
|
2; |
|
A |
|
|
|
1 |
4 |
|
4 |
|
1 |
|
|
4; A |
|
|
1 |
5 |
|
1 |
|
1 |
|
|
7; |
|
|||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
23 |
|
|
|
1 |
|
6 |
|
|
|
|
|
31 |
|
|
|
|
|
|
|
|
8 |
|
3 |
|
|
|
32 |
|
|
|
|
|
4 |
3 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
A |
1 6 |
|
|
|
1 |
|
4 |
|
24. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
33 |
|
|
|
|
|
|
4 |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, имеем следующую обратную матрицу:
|
1 |
2 |
2 |
4 |
||
A 1 |
11 |
1 |
7 |
|||
|
|
|||||
10 |
||||||
|
32 |
2 |
24 . |
|||
|
|
|
||||
15

|
|
|
Тогда матричное решение исходной системы X |
|
A 1 B имеет вид: |
|
|||||||||||||||||||||||
|
|
|
x1 |
1 |
|
|
2 |
|
2 |
|
4 |
7 |
|
1 |
|
2 |
7 |
2 |
9 |
4 8 |
|
|
|||||||
X |
|
x2 |
|
11 |
|
1 |
|
|
|
7 |
9 |
|
|
11 7 1 9 |
|
|
7 8 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
10 |
|
|
|
10 |
|
|
|
|
|
||||||||||||||||||||
|
|
|
x3 |
|
32 |
2 |
|
24 |
8 |
|
|
32 |
7 |
2 |
9 |
24 8 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
14 |
18 |
|
32 |
|
|
|
|
|
0 |
|
|
|
|
0 |
|
0 |
|
|
|
|
|
||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
77 |
|
9 |
56 |
|
|
|
|
30 |
|
|
|
|
30 |
|
3 . |
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
10 |
|
|
|
|
10 |
|
|
|
|
|
10 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
224 |
18 |
|
192 |
|
|
50 |
|
|
|
|
5010 |
5 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
Проверка: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
Подставим |
найденные |
числа |
вместо |
переменных |
x1 , x2 , x3 |
в исходную |
систему |
|||||||||||||||||||
|
|
|
|
|
|
1 0 |
4 3 |
1 |
|
|
5 |
0 |
|
12 |
|
|
5 |
7; |
|
|
|
|
|
|
|||||
уравнений |
4 0 |
8 3 |
3 |
|
|
5 |
0 |
|
24 |
15 |
9; |
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
1 0 |
|
6 3 |
2 |
|
|
|
5 |
0 |
|
18 |
|
|
10 |
8. |
|
|
|
|
|
|
|||
|
|
|
Получили верные числовые равенства, следовательно, решение найдено |
||||||||||||||||||||||||||
верно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Ответ: |
x1 |
0, x2 |
3, |
x3 |
5 . |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
Метод Крамера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
Рассмотрим |
|
решение |
системы |
(2.1) с |
помощью |
формул |
Крамера |
|||||||||||||||||||
x |
|
1 |
, x |
|
|
|
2 |
, ... |
|
, |
|
x |
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|||||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
Дополнительные определители |
|
n n |
1, 2, 3, ... |
получаются из основного Δ, |
||||||||||||||||||||||
если в нём заменить соответственно первый, второй, …n-й столбец на столбец свободных членов системы.
Таким образом, для решения системы (2.1) с учетом уже введённых
обозначений, |
дополнительные определители будут иметь вид: |
||||||||||||||||||
|
b1 |
a12 |
a13 |
|
|
|
|
a11 |
b1 |
a13 |
|
|
|
|
a11 |
a12 |
b1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
1 |
b2 |
a22 |
a23 |
|
, |
2 |
|
a21 |
b2 |
a23 |
|
, |
3 |
|
a21 |
a22 |
b2 |
|
|
|
b3 |
a32 |
a33 |
|
|
|
|
a31 |
b3 |
a33 |
|
|
|
|
a31 |
a32 |
b3 |
|
. |
|
|
|
|
|
|
||||||||||||||
Пример 6. |
Решить систему уранений, |
рассмотренную в примере 5, по |
|||||||||||||||||
правилу Крамера. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
16

|
1 |
4 |
1 |
|
|
7 |
4 |
1 |
|
|
|
|
1 |
7 |
1 |
|
|
|
|
1 |
4 |
7 |
|
|||||
|
4 |
8 |
3 |
10; |
1 |
9 |
8 |
3 |
|
0; |
|
2 |
4 |
9 |
3 |
30; |
3 |
|
4 |
8 |
9 |
50; |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 |
6 |
2 |
|
|
8 |
6 |
2 |
|
|
|
|
1 |
8 |
2 |
|
|
|
|
1 |
6 |
8 |
|
|||||
1 |
0 |
|
|
|
|
2 |
30 |
|
|
|
|
|
|
3 |
|
50 |
|
|
|
|
|
|
||||||
x1 |
|
|
|
|
0; |
x2 |
|
|
|
|
|
|
3; |
|
x3 |
|
|
|
|
|
|
|
5. |
|
|
|
|
|
|
10 |
|
|
|
10 |
|
|
|
|
|
|
10 |
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Тема 3. |
Теория пределов |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
Предел функции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пусть функция y |
f |
x |
определена в некоторой окрестности точки x0 . |
|
|
|
|||||||||||||||||||||||
|
Определение. |
Число A называется пределом функции |
f x |
в точке x0 |
(или при |
|||||||||||||||||||||||||
x |
|
x0 ), |
если |
для |
любого, сколь угодно малого положительного числа |
0 |
||||||||||||||||||||||||
найдётся |
такое положительное |
число |
|
0 , |
зависящее |
от |
, что для |
всех |
x , |
|||||||||||||||||||||
удовлетворяющих условию |
|
x |
x0 |
|
, |
x |
x0 выполняется неравенство |
|
f (x) A |
|
|
|||||||||||||||||||
|
|
|
|
|
||||||||||||||||||||||||||
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Этот предел функции обозначается: |
lim |
f (x) |
A или ƒ(х)→А при х→х0. |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
x0 |
|
|
|
|
|
|
|
|
|
|
|
Практическое вычисление пределов основывается на следующих теоремах: |
|
||||||||||||||||||||||||||||
если существуют |
lim |
f (x) |
|
А и |
|
lim |
g (x) |
B , то |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
1) |
lim [ f (x) |
g(x)] |
lim f (x) |
|
lim g(x) |
|
A |
B ; |
|
|
|
|
|
(3.1) |
|
|||||||||||||||
|
x |
a |
|
|
|
|
x |
|
|
a |
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
||||
2) |
lim [ f (x) g(x)] |
lim |
f (x) |
lim g(x) |
A |
B ; |
|
|
|
|
|
|
(3.2) |
|
||||||||||||||||
|
x |
a |
|
|
|
|
x |
|
a |
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3) |
lim [cf (x)] |
c |
lim |
f (x) |
|
c |
A; |
|
|
|
|
|
|
|
|
|
|
(3.3) |
|
|||||||||||
|
x |
a |
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
lim |
f (x) |
|
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
4) |
lim |
x |
a |
|
|
|
|
(при lim g x |
0 ). |
|
|
|
|
|
(3.4) |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
x |
a g(x) |
lim g(x) |
|
B |
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
x |
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определение. Функция α (х) называется бесконечно малой величиной при |
|
||||||||||||||||||||||||||||
х→х0, или при х→∞, если её предел равен нулю lim |
(x) |
0 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
|
|
|
|
|
|
|
Определение. Функция ƒ(х) называется бесконечно большой в точке х0 (или |
|
||||||||||||||||||||||||||||
при х→х0), если имеет место одно из равенств: lim |
f (x) |
; |
lim f (x) |
. |
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x0 |
|
|
x x0 |
|
|
|
||
17

Теорема (о связи бесконечно большой и бесконечно малой функций) : |
если |
||||||||||||||
ƒ(х) ─ бесконечно малая функция при х→х0, то |
1 |
|
─ бесконечно большая |
||||||||||||
|
|
||||||||||||||
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
||
функция при х→х0, и наоборот. |
|
|
|
|
|
|
|
|
|
|
|
|
|||
Первый замечательный предел |
lim |
sin x |
1. |
|
|
|
|
|
(3.5) |
||||||
|
x |
|
|
|
|
|
|||||||||
|
|
|
|
x |
0 |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
x |
|
|
|
1 |
|
|
Второй замечательный предел |
|
1 |
1 |
|
|
1 |
|
e 2,71828 . |
(3.6) |
||||||
|
|
|
|
||||||||||||
lim |
|
|
|
lim |
|
||||||||||
|
x |
||||||||||||||
|
|
|
|
x |
|
|
|
0 |
|
|
|
|
|
||
Пример 7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти предел |
lim |
x 3 |
2x 3 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
5x 1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
x 3 |
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение: Поскольку функция непрерывна в точке x |
|
3 , искомый предел равен |
|||||||||||||
значению функции в этой точке. Используя теоремы о действиях над пределами функций, получим
lim |
x 3 |
2x 3 33 |
2 3 3 27 6 3 24 3 |
. |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
5x 1 |
|
|
5 3 1 |
|
|
15 1 |
|
16 2 |
||||||
x 3 |
|
|
|||||||||||||
Пример 8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Найти предел lim |
2x |
7 |
|
. |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
x 6 x 2 |
5x |
6 |
|
|
|
|
|
|
|||
Решение: |
При x |
6 числитель 2x |
7 стремится к пяти 2 6 7 12 7 5 (т.е. |
||||||||||||
является ограниченной функцией), а знаменатель x 2 5x 6 – к нулю (т.е. является бесконечно малой величиной). Очевидно, что их отношение есть величина бесконечно большая, т. е.
– к нулю (т.е. является бесконечно малой величиной). Очевидно, что их отношение есть величина бесконечно большая, т. е.
lim |
2x 7 |
lim |
|
2 6 |
7 |
|
12 7 |
5 |
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
x 6 x2 5x 6 x 6 62 |
5 6 6 |
|
36 30 6 0 |
|
|
|
|
|
|
|
|||||||||
В рассмотренных примерах предел находился сразу, |
чаще при вычислении |
||||||||||||||||||
пределов мы сталкиваемся с неопределённостями: |
0 |
|
|
|
|
, 1 . |
|||||||||||||
|
|
|
|
||||||||||||||||
0 , |
, |
||||||||||||||||||
Пример 9. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Найти предел |
lim |
2x 2 |
16 x |
24 |
. |
|
|
|
|
|
|
|
|
|
|
||||
|
x 3 |
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
18

Решение: При |
x |
2 |
числитель и |
знаменатель дроби равны нулю, имеем |
||||||
неопределенность |
вида |
|
0 |
. Чтобы |
раскрыть неопределённость вида |
|
0 |
|
||
0 |
0 , |
|||||||||
|
|
|
|
|
||||||
необходимо разложить |
числитель и знаменатель на множители и сократить |
их на |
||||||||
общий множитель |
x |
2 . |
|
|
|
|
|
|
||
lim |
|
2x 2 |
|
16x 24 |
|
|
|
0 |
|
|
|
|
|
|
lim |
|
|
|
|
2 x 2 x 6 |
|
|
|
lim |
|
|
|
2 x 6 |
|
|
|
|
|
|
|
2 |
. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||||||||
x 2 |
x |
|
8 |
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
x 2 x |
|
|
|
|
2x 4 |
|
|
|
x 2 x |
|
2x 4 |
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Пример 10 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Найти предел |
|
lim |
|
|
|
|
|
|
|
x2 |
16 |
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
5 |
|
x |
|
|
|
2x |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
Решение: Непосредственная подстановка предельного значения |
|
|
аргумента |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
x |
4 |
|
приводит к неопределённости вида |
|
0 |
|
. Избавимся от иррациональности в |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
0 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
знаменателе, |
|
|
умножив |
|
|
|
числитель |
|
|
|
|
|
|
и |
|
знаменатель |
|
|
|
дроби |
|
|
на |
выражение |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
16)( |
|
|
5 x |
|
|
|
|
2x |
7 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
5 |
|
x |
|
2x |
7 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 4 ( 5 x |
|
|
2x 7 )( 5 x |
|
2x 7 ) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
lim |
|
|
16 5 x |
|
|
|
|
2x 7 |
|
|
|
|
|
|
|
lim |
16 5 x |
|
2x 7 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
x |
|
|
|
2x |
7 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
x |
4 |
|
|
|
|
5 |
|
x |
|
|
|
|
|
2x |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
lim |
16 5 x |
2x 7 |
|
|
|
|
|
|
|
|
lim |
|
x 4 x 4 5 x |
|
|
|
2x 7 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3x |
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
x |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
x |
4 |
5 |
|
|
|
x |
|
|
|
2x |
7 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16 |
. |
|||||||||||||||||||||||||||||||||||
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
x |
4 |
5 |
|
|
|
x |
|
|
2x |
7 |
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
x |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|||||||||||||||
|
|
|
|
Пример 11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
lim |
|
2x 2 |
|
|
3x |
|
|
|
|
|
4 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
x 4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
x |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
Решение: Теорему о пределе частного здесь применить нельзя, так как |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
числитель и |
|
знаменатель дроби конечного предела не имеют. |
В данном случае |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
имеет |
место |
|
|
неопределённость |
|
|
вида |
|
|
|
|
|
|
|
. |
|
Разделим |
|
числитель |
|
|
и знаменатель |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
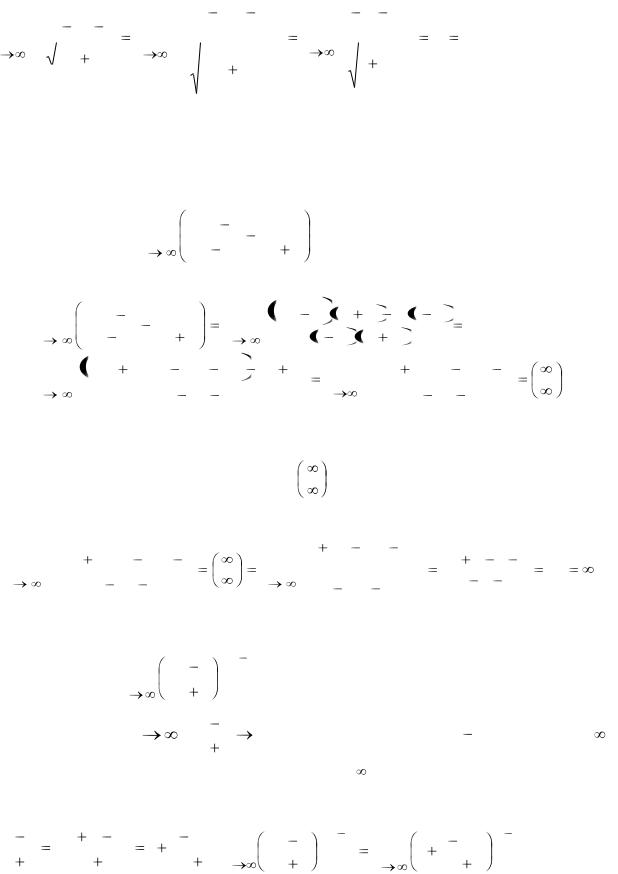
дроби на х в высшей степени (в данном случае на х2 ), а затем воспользуемся теоремами о пределах функций:
19
|
|
|
|
|
|
|
|
2x 2 |
|
|
|
3x |
|
|
|
4 |
|
|
2 |
|
3 |
|
4 |
|
|
|
|
||||||||
|
2x 2 |
3x 4 |
|
|
x 2 |
|
|
|
x 2 |
|
|
|
x 2 |
|
|
x |
|
|
x 2 |
2 |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
lim |
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||
|
|
4 |
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|||||||||||||
x |
|
x |
1 |
x |
|
|
x |
|
1 |
|
|
|
|
x |
|
1 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
x |
4 |
|
x |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 12
Найти предел |
lim |
3x 2 |
4 |
5 |
. |
|
x |
3 |
|
4x 6 |
|||
x |
|
|
|
|||
Решение: Приведём дроби к общему знаменателю:
|
lim |
|
3x 2 |
4 |
|
5 |
|
|
lim |
|
3x 2 4 4x 6 5 x 3 |
|
|
|
|
|||
|
|
x 3 |
|
|
4x 6 |
|
|
x 3 4x 6 |
|
|
|
|
|
|||||
x |
|
|
|
|
x |
|
|
|
|
|
|
|
||||||
|
lim |
12x 3 |
18x 2 |
16x |
24 |
5x 15 |
lim |
12x 3 18x 2 21x 9 |
|
|
; |
|||||||
|
|
|
|
4x 2 |
|
|
|
|
|
4x 2 |
|
|
|
|
||||
x |
|
|
|
|
6x 18 |
|
|
x |
6x 18 |
|
|
|
||||||
Числитель и знаменатель дроби – бесконечно большие функции, поэтому здесь
имеет |
|
место |
|
неопределённость |
вида |
|
|
|
|
. |
|
Раскрывая |
эту |
неопределённость, |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
разделим числитель и знаменатель дроби на высшую степень x , т. е. на x3 : |
|
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
18 |
|
21 |
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
12 x 3 |
18x 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
21x 9 |
|
|
|
|
|
|
|
x |
|
|
x 2 |
|
|
|
x 3 |
12 0 0 0 12 |
|
||||||||||||||||||||||||||||||
|
lim |
|
|
|
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
. |
|||||||||||||||||||||||||||||
|
|
|
4x |
2 |
6x |
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
6 |
|
|
18 |
|
|
|
|
|
0 |
0 |
0 |
|
|
0 |
|||||||||||
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
x |
2 |
|
x |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Пример 13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
2x |
9 |
|
|
x |
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
Найти предел lim |
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
2x |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
Решение: При x |
|
|
|
2x |
9 |
|
|
|
1, а показатель степени (x |
5) |
стремится к , |
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
2x |
9 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
следовательно, имеем неопределённость вида |
1 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
Представим дробь в виде суммы 1 и некоторой бесконечно малой величины: |
||||||||||||||||||||||||||||||||||||||||||||||||
|
2x 9 2x 9 18 |
1 |
|
|
18 |
|
. lim |
|
2x 9 x2 5 |
|
|
lim 1 |
18 |
|
x 5 |
. |
|
|
|
||||||||||||||||||||||||||||||
|
2x 9 |
|
|
2x 9 |
|
|
2x 9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
2x 9 |
|
|
|
|
|
|
|
|
2x 9 |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
Применим второй замечательный предел |
(3.6). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
20
