
5628
.pdf
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
а) |
lim |
|
n un |
|
|
lim |
n |
= lim |
0 , |
|
|
0 |
|
1 |
|
|
ряд сходится. |
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
nn |
|
|
n |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3n |
2 |
|
|
|
|
|
3n |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
б) |
lim |
|
n un |
|
|
lim n |
|
|
|
|
|
lim |
3, |
3 |
1 |
|
ряд расходится. |
|
|||||||||||||||||||||||||||||||
|
|
n |
1 |
|
|
|
|
|
|
|
|
n |
1 |
|
|
||||||||||||||||||||||||||||||||||
|
n |
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
Интегральный признак. Если члены знакоположительного ряда |
u n |
могут |
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
быть |
|
представлены, |
как |
числовые |
|
значения |
некоторой |
функции |
|||||||||||||||||||||||||||||||||||||||||
f(x): u1=f(1), u2=f(2), u3=f(3),… un |
f (n)... и функция f(x) ─ непрерывная, монотонно |
||||||||||||||||||||||||||||||||||||||||||||||||
убывающая на интервале (1; + ), то: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
если |
f(x)dx сходится, то сходится и ряд (1); |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
если |
f(x)dx расходится, то расходится так же и ряд (1). |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Признак сравнения. Пусть даны два знакоположительных ряда |
|
|
u n |
и |
vn , |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
n 1 |
|
для всех n выполняется неравенство |
|
|
|
|
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
то если ряд |
vn сходится, то и ряд |
u n |
сходится, |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
если ряд |
|
|
u n |
расходится, то и ряд |
vn |
расходится. |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
Для сравнения часто используются «эталонные» ряды: |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
Геометрический ряд |
|
|
|
аn q n 1 – сходится при |
|
q |
|
|
|
1, расходится при |
|
q |
|
1. |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Гармонический ряд |
|
|
|
|
1 |
|
– расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
n |
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Обобщённый гармонический ряд |
1 |
|
|
1 |
|
1 |
1 |
|
... |
1 |
|
... ,сходится при |
1, |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 n |
|
|
|
2 |
3 |
|
|
|
|
n |
|
|
|
|
|
|
|
||||||
расходится при |
|
|
1. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Знакочередующиеся ряды. |
|
|
|
|
|
|
||||||||||||||||||||
|
Определение. Знакочередующимся рядом называется ряд вида |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
u1 - u2 + u3 - u4 +…+(-1)n+1un + …= |
(-1)n 1un . |
|
|
|
|
|
(8.2) |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
Признак Лейбница. Знакочередующийся ряд сходится, если выполняются два |
||||||||||||||||||||||||||||||||||||||||||||||||
условия : |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
1)последовательность абсолютных величин членов ряда монотонно убывает, |
||||||||||||||||||||||||||||||||||||||||||||||||
|
т.е. |
|
u1 |
|
|
|
u2 |
|
|
u3 |
|
|
|
... |
|
un |
|
... |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
41

2) общий член ряда стремится к нулю lim un 0 .
n
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(-1)n 1 |
|
|
|
|
|
|
|
|
|
||||||||
|
Пример 38. |
|
Исследовать ряд на сходимость n 1 |
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
(2n -1) 2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Решение: Проверим выполнение условий признака Лейбница |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 ; |
|
|
|
|
u |
2 |
|
|
|
|
|
( 1)2 1 |
|
|
|
|
|
|
1 |
|
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
u |
|
|
|
( 1)1 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
1 |
|
|
|
2 1 |
1)2 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
1)2 |
|
|
|
|
|
9 |
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u3 |
|
|
|
1)3 1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
... |
|
члены ряда убывают по абсолютной величине. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
( |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
3 |
1) |
2 |
|
|
|
|
25 |
|
|
|
|
25 |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
2) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
0 , условия признака |
Лейбница выполняются, |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
lim |
|
un |
|
|
|
lim |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1)2 |
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
n |
|
(2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
данный ряд сходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
Пример 39. |
|
Исследовать сходимость ряда |
( |
1)n |
|
|
n |
. |
|
|
|
|
|
|
Решение: |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
1 |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
1) |
|
|
|
|
|
|
|
1 |
|
1 |
|
|
|
|
|
|
|
|
|
1 |
|
|
1 |
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
|
|
|
2 |
; |
|
|
|
|
|
|
|
|
|
3 |
|
3 |
|
3 |
|
члены |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
u1 |
|
|
( |
1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
u2 |
|
|
|
|
( |
1) |
|
|
|
|
|
|
|
|
|
|
|
u3 |
|
|
( 1) |
|
|
|
|
|
|
... |
||||||||||||||||||
|
|
|
|
1 |
1 |
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
|
|
|
2 |
1 |
|
|
|
3 |
|
3 |
1 |
4 |
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
ряда убывают по абсолютной величине; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
2) |
|
|
lim |
|
n |
|
|
1 |
0 |
, второе условие признака Лейбница не выполняется, ряд |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
n |
1 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Степенные ряды |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
Определение. |
Ряд вида a |
0 |
+ a |
x+ a |
x2+…+a |
x n |
= |
|
|
|
а |
xn |
– |
|
|
|
|
|
(8.3) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
n |
|
|
|
+… |
|
n |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
называется степенным. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Числа a0, a1,… a2, …an …называются коэффициентами ряда, |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
x R ─ действительная переменная. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
|
Теорема. Степенной ряд (13) сходится при значениях х, содержащихся в |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
некотором интервале (-R, R) |
и расходится при значениях х вне этого интервала. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Этот интервал называется интервалом сходимости, а число R ─ радиусом |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
сходимости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
Формула для вычисления радиуса сходимости степенного ряда |
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
|
lim |
|
|
|
an |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(8.4) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
an 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
42

Пример 40. |
Определить радиус сходимости степенного ряда и исследовать его |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
xn |
|
|
|
|
|
|
|
|
|
|
|
|||||||
сходимость на концах интервала n 1 |
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3n (n 1) |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
Решение: |
Найдём коэффициенты |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
an |
1 |
|
, |
an 1 |
|
1 |
|
|
1 |
|
|
|
; |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
3n (n 1) |
|
|
|
|
|
3n 1 ((n 1) 1) 3n 1 (n 2) |
|
|
|
|
|
|
|
||||||||||||||||||
Найдем R |
|
lim |
|
an |
|
; R |
lim |
|
3n 1(n 2) |
|
lim |
|
|
3(n 2) |
|
3. |
||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
an 1 |
|
|
3n (n 1) |
|
|
n 1 |
|
|||||||||||||||||||||||
|
|
n |
|
|
|
|
n |
|
|
n |
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
R=3, значит ряд сходится на интервале (-3; 3). Исследуем сходимость ряда на |
||||||||||||||||||||||||||||||||
концах интервала. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При x = 3, получаем ряд n 0 |
3n |
1 |
, ряд расходится, как |
|
|
|||||||||||||||||||||||||||
3n (n 1) |
|
|
n 0 |
n 1 |
|
|
||||||||||||||||||||||||||
гармонический. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
При x = -3, получаем знакочередующийся ряд |
( 1)n 3n |
|
|
( 1)n |
|
, этот ряд |
||||||||||||||||||||||||||
3n (n 1) |
n 0 n 1 |
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 0 |
|
|
|||||||||||
сходится (по признаку Лейбница). Таким образом, ряд сходится для всех x  3; 3 .
3; 3 .
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2n (x |
1)n |
|||
Пример 41. |
|
Найти область сходимости степенного ряда |
|
|
|
. |
|||||||||||||||||||||||||||||||||||||||||||||
2n |
1 |
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|||||||
Найдём радиус сходимости |
an |
|
|
|
2n |
|
|
|
, |
an 1 |
|
2 n 1 |
|
2 n 1 |
, |
|
|
||||||||||||||||||||||||||||||||||
|
|
2n |
1 |
|
2(n |
1) 1 |
|
2n |
1 |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
R lim |
|
|
an |
|
|
|
|
lim |
|
2 n |
|
|
|
2(n 1) 1 |
|
|
|
lim |
|
2 n |
2n 2 1 |
|
lim |
2n 1 |
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
an 1 |
|
|
|
|
2n |
1 |
|
|
|
|
2 n 1 |
|
|
|
|
2n 1 |
2 n |
|
|
|
|
2(2n 1) |
|||||||||||||||||||||||||||||
n |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
n |
|
2 |
|
|
|
n |
|
|||||||||||||||||||||||||||
lim |
2n |
1 |
|
|
|
|
2 |
|
1 |
|
|
; |
R |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
4n |
2 |
|
|
|
4 |
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
1 |
|
x |
1 |
|
1 |
, |
|
|
3 |
|
|
x |
|
1 |
─ интервал сходимости. |
|
|
|
|
||||||||||||||||||||||||||||||
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Исследуем сходимость ряда на концах интервала. |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
n |
|
1 n |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
При |
|
x |
|
1 |
, |
получим ряд |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
2 |
|
|
|
n 1 |
|
|
2n 1 |
|
n 1 2n 1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Для исследования ряда на сходимость воспользуемся интегральным признаком
1
сходимости, в качестве функции f(x) возьмём функцию 2x 1 .
43

Несобственный интеграл |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
dx |
|
|
|
|
|
1 |
|
|
1 |
ln( 2 1 1)) |
|
|
1 |
|
ln |
|
2b |
|
|
|
|
|||||||
|
|
lim ( |
ln |
2b 1 |
|
|
lim |
|
1 |
|
|
расходится , |
|||||||||||||||||
1 2x 1 |
|
2 |
2 |
2 |
|
||||||||||||||||||||||||
|
b |
|
|
|
|
|
|
|
b |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
следовательно и ряд расходится. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2n |
1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 n |
|
|
|
|
|
|||||
|
При |
x |
|
3 |
|
получим ряд |
2 |
|
|
|
|
|
, по признаку Лейбница ряд |
||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
2 |
|
2n 1 |
|
n 1 2n 1 |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|
|
|
||||||||||||||
сходится, таким образом, интервал сходимости |
|
3 |
|
|
x |
1 |
. |
||||||||||||||||||||||
2 |
|
|
2 |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Примерные варианты аудиторной контрольной работы для студентов заочного отделения 1 курс
Вариант 1
1. Даны вершины треугольника ABC.
А(–3; 9), В(4; –2), С(7; 6).
Найти уравнение стороны AB;
2. Уравнение кривой привести к каноническому виду и построить линию.
x2 |
|
|
4y2 |
8x 8y 24 0. |
||
3. Найти предел. |
|
|||||
lim |
3x2 |
5x 2 |
; |
|||
3x |
1 |
|||||
x |
1 |
|
|
|||
|
|
|
|
|
||
3 |
|
|
|
|||
|
|
|
|
|||
4. Найти а производную функции
|
|
|
y |
ln x x tg 2 3x |
|
Вариант 2
1.Даны вершины треугольника ABC.
А(2; 8), В(–6; –2), С(4; 2).
Найти: уравнение медианы BM, проведённой из вершины B к стороне AC
2.Уравнение кривой привести к каноническому виду и построить линию.
x2 4y2 8x 8y 24 0.
44
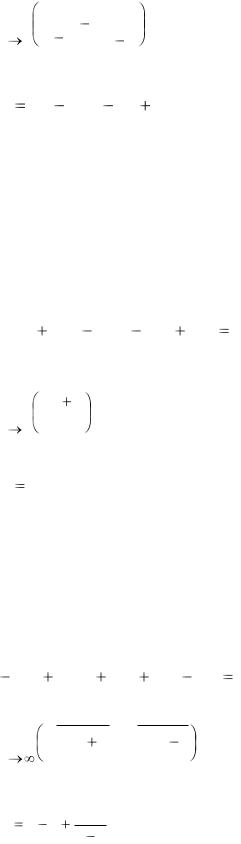
3. Найти предел.
lim |
1 |
|
|
4 |
|
; |
|
|
|
|
|
||
x 2 |
|
x2 |
|
4 |
||
x 2 |
|
|
|
4. Исследовать функцию на экстремумы y x3 4x 2 3x 6
Вариант 3
1.Даны вершины треугольника ABC.
А(8; 1), В(–2; –1), С(4; –11)
Найти уравнение высоты АD, проведённой из вершины А к стороне ВС
2.Уравнение кривой привести к каноническому виду и построить линию.
16x2 |
9y2 192x 90 y 657 0; |
|||||
4. |
Найти предел. |
|||||
|
|
|
|
3 |
|
|
|
|
8x 3 |
|
|
||
lim |
x . |
|||||
|
|
|||||
3 |
|
|||||
x |
0 |
|
|
|
||
5. Найти интервалы монотонности функции y 2x ln x
Вариант 4
1. Даны вершины треугольника ABC А(–1; 7), В(–2; –5), С(8; 2).
Найти уравнение прямой, проходящей через точку А параллельно стороне ВС. 2. Уравнение кривой привести к каноническому виду и построить линию.
4x2 25 y2 24x 50 y 111 0.
4. Найти предел.
lim 
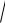 2x2 5
2x2 5 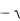
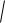 2x2 1 ; x
2x2 1 ; x
5. Найти интервалы выпуклости и точки перегиба функции
y x 2
4
x 2
45

Примерные варианты аудиторной контрольной работы для студентов заочного отделения 2 курс
Вариант 1
1. Найти интеграл :
а) |
( |
2 |
3x |
|
|
4 |
|
|
)dx |
x |
|
|
|
|
|
||||
|
|
2 |
|||||||
|
|
1 |
9x |
|
|
||||
|
|
|
|
|
|
||||
2. Решить дифференциальное уравнение.
(1 x)dx ( y 2)dy 0
3. Исследовать ряд на сходимость. n
n 1 (n 1)3n
4. Решить систему уравнений матричным методом
4x1 2x2 3x3 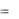 4; 3x1 x2 2x3 11; 2x1 3x2 x3 15.
4; 3x1 x2 2x3 11; 2x1 3x2 x3 15.
Вариант 2
1. Найти интеграл :
x 2 (1 x 2 |
1 |
|
)dx |
|
|
|
|
||
|
|
|
||
|
|
x |
||
3. Решить дифференциальное уравнение. y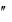 y
y 2 y x 2
2 y x 2
4. Исследовать ряд на сходимость n3
n 1 2n
5. Решить систему уравнений методом Крамера
4x1 x2 8x3  8; 4x1 6x2 3x3 12; x1 2x2 4x3 11.
8; 4x1 6x2 3x3 12; x1 2x2 4x3 11.
46

Вариант 3
1. Вычислить площадь фигуры, ограниченной линиями. y 12 (x 5) 2 ; 2x y 10 0
2. Решить дифференциальное уравнение. y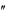 4 y
4 y 5y 0
5y 0
3. Исследовать ряд на сходимость.
( 1)n
n 1 2n (3n 1)
4. Решить систему уравнений методом Крамера
2x1 5x2 8x3 9; 3x1 3x2 2x3 8; x1 2x2 4x3 5.
Вариант 4
1. Найти интеграл
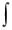 x ln xdx
x ln xdx
2. Решить дифференциальное уравнение
y |
3y |
x |
|
|
|||
x |
|||
|
|
3. Исследовать ряд на сходимость.
(2n 1)!
n 1 n!
4. Решить систему уравнений матричным методом
x1 5x2 7x3 4; 3x1 x2 4x3  7; x1 2x2 3x3 1.
7; x1 2x2 3x3 1.
47
Тренировочный тест по математике
Вариант 1
Задание 1 . Прямые y=3x+8 и y=kx+6 перпендикулярны, если угловой коэффициент k равен…
Варианты ответов:
1) k=-7; 2) k=-5; 3) k= -1/3 ; 4) k=-2.
Задание 2.
Скалярное произведение векторов 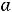 = 3
= 3
 5
5 
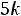 и
и  =
= 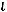

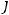

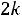 равно…
равно…
Варианты ответов:
1) 8; 2 ) 10; 3) 5; 4) 15.
Задание 3. Алгебраическое уравнение второй степени 
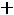

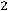

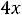

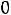 задаёт на плоскости кривую…
задаёт на плоскости кривую…
Варианты ответов:
1) окружность; 2) параболу; 3) эллипс; 4) гиперболу.
Задание 4. Если А= , В= , то матрица А+В имеет вид…
Варианты ответов: 1) |
2) |
3) |
; 4) |
. |
||
Задание 5. Определитель |
|
|
равен… |
|
|
|
Варианты ответов: 1) 4; 2) -10; |
3) 23; |
г) 7. |
|
|
||
Задание 6. |
|
|
|
|
||
Относительно решения системы линейных уравнений можно утверждать :
Варианты ответов:
1)имеет два решения;
2)не имеет решений;
3)имеет единственное решение;
4)имеет бесконечное множество решений.
Задание 7. Вычислить |
lim |
3x2 |
5x |
8 |
|
5x2 |
x |
2 |
|||
|
x |
48

Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) |
|
; 2) |
3; |
3) 5; |
4) |
|
|
; |
5) 0. |
|
|
|
( 1)n |
1 |
|
||||||||
|
|
||||||||||||||||||||||
Задание 8. |
Для исследования ряда |
|
|||||||||||||||||||||
3n |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n 1 |
|
|
|||||
применим признак сходимости......... |
|
|
|
|
|||||||||||||||||||
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) Лейбница ; |
2) интегральный; 3) сравнения; 4) Даламбера |
||||||||||||||||||||||
Задание 9. |
Производная функции |
|
|
|
|
равна |
|||||||||||||||||
|
|
||||||||||||||||||||||
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
1) |
|
|
|
; |
2) ) |
|
; |
3) |
|
|
|
; 4) |
|
. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||
Задание 10. Частное решение дифференциального уравнения у'= 2х+1, начальным условием у(0)=3
Варианты ответов:
1) 3; 2) y=x2+x+3 ; 3) y=2x+3; 4) 1.
Вариант 2
Задание 1.
Если А= |
, В= |
, то матрица А∙В имеет вид : |
|
Варианты ответов: |
|
|
|
1) |
; 2) |
; 3) |
; 4) |
Задание 2. |
Определитель |
|
равен : |
Варианты ответов: 1) 5; 2) 8; 3) 12; 4) 25.
Задание 3. Решение системы линейных уравнений
методом Крамера имеет вид:
Варианты ответов:
49

а) х= |
|
, у= |
|
; |
б) х= |
|
, у= |
|
; |
|
|
|
|
в) х= |
|
, у= |
|
|
; |
г) х= |
|
|
, у= |
|
. |
|
|
|
|
|
|
||||||
Задание 4. При |
каком значении β векторы |
= 2 3 |
и |
||||||||
= 4 |
|
|
|
коллинеарные : |
|
|
|
|
|
|
|
Варианты ответов: |
|
|
|
|
|
|
|||||
1) 1; |
2) 3; |
3) |
5; |
4) 2. |
|
|
|
|
|
|
|
Задание 5. . Уравнение прямой, параллельной прямой y=x+3 и проходящей через точку N(1;2), имеет вид:
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) y = 3x; |
2) y = x+1; 3) y = x-8; 4) y = |
|
x-4. |
|||||||||||||||||||
|
||||||||||||||||||||||
Задание 6. Уравнение окружности с центром в точке С(1;-2) и радиусом R=4 |
||||||||||||||||||||||
имеет вид: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) |
|
|
|
|
|
|
|
|
; |
|
2) |
|
|
|
; |
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
3) |
|
|
|
|
|
|
|
|
; |
|
4) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
lim |
|
x2 |
4x 3 |
||||||||||
Задание 7. |
Вычислить |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
x3 1 |
||||||||||||||||||||
x |
1 |
|
||||||||||||||||||||
Варианты ответов: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
1) 0; 2) |
; 3) |
|
; |
4) |
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Задание 8. Ряд |
|
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 n |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Варианты ответов:
1) сходится; 2) расходится; 3) условно сходится; 4) условно расходится
Задание 9. Угловой коэффициент касательной, проведенной к графику
функции y=3x3+5x2-6x+7 в точке х0=1, равен ...
Варианты ответов:
50
