
5572
.pdf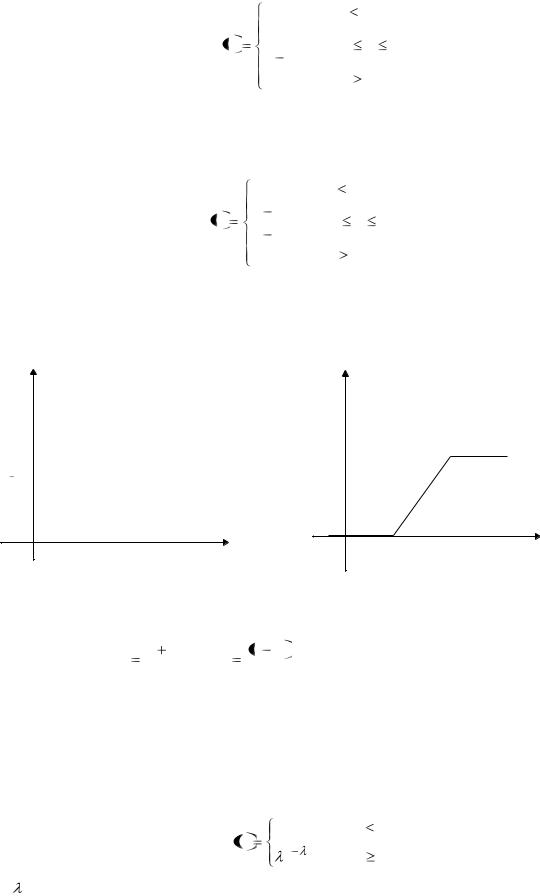
|
0, |
|
при x |
a, |
|
|
f x |
|
|
1 |
, при a |
x |
b, |
|
|
|
||||
|
b |
a |
||||
|
0, |
|
при x |
b. |
||
Функция распределения примет вид:
|
0, |
|
при x |
a; |
|
F x |
|
x |
a |
, при a |
x b; |
|
b |
a |
|||
|
|
|
|
||
|
1, |
|
при x |
b. |
|
Графики обеих функций изображены на рисунке 1.4.
f(x) |
F(x) |
1 |
|
|
|
|
|
|
|
|
|
|
1 |
||
|
|
|
|
|
||
b a |
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
a |
b |
x |
|
0 |
a |
b |
x |
|||||||
|
|
|
|
|||||||
Рисунок 1.4 − Графики функций F(x) и f(x)
M(X) и D(X) равномерно распределенной случайной величины рассчитываются
по формулам M (X ) |
a |
b |
|
b a 2 |
|
|
|
; D(X ) |
|
. |
|
|
2 |
12 |
|||
|
|
|
|
||
Показательное распределение Показательным (экспоненциальным) называют распределение вероятностей
случайной величины X, которое описывается плотностью
0 |
при x |
0; |
f x |
x при x |
|
e |
0, |
где − постоянная положительная величина.
31
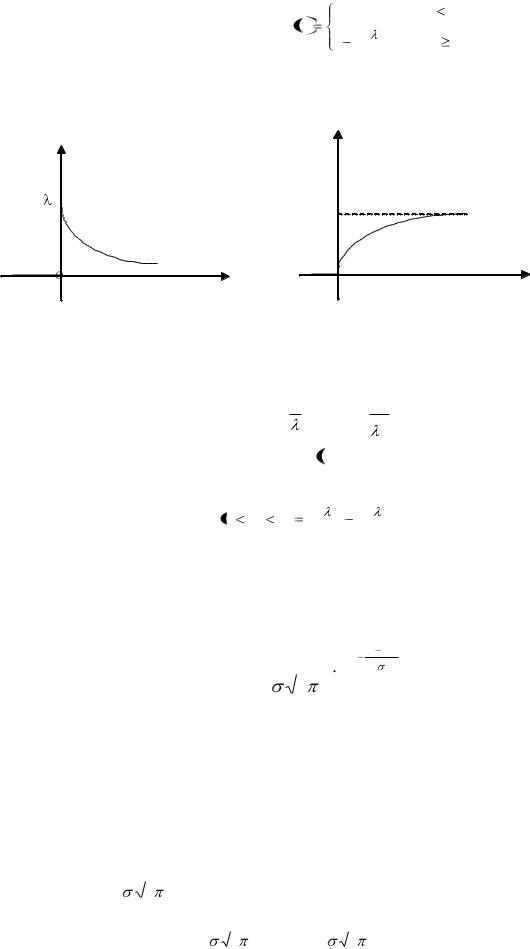
Функция распределения примет вид: F x
0, при x 0; 1 e x , при x 0.
x , при x 0.
Графики плотности и функции распределения показательного закона
F(x)
f (x)
1
0 |
x |
0 |
x |
Рис. 1.5− Графики функций F(x) и f(x)
Для M(X) и D(X) показательного распределения справедливы равенства
M ( X ) 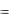 1 ; D( X )
1 ; D( X ) 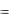 12 .
12 .
Вероятность попадания в интервал a; b показательно распределённой случайной величины вычисляется по формуле
показательно распределённой случайной величины вычисляется по формуле
P a X b e
e a e
a e b .
b .
Нормальное распределение
Непрерывная случайная величина Х распределена по нормальному закону, если ее плотность распределения вероятностей выражается формулой
f(х) = |
1 |
|
e |
||
|
|
|
|||
|
|
|
|||
2 |
|||||
|
|
|
|||
( x a)2
2 2 ,
где a − математическое ожидание, 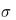 − среднее квадратическое отклонение. График плотности нормального распределения называют нормальной кривой
− среднее квадратическое отклонение. График плотности нормального распределения называют нормальной кривой
или кривой Гаусса (рисунок 1.6).
1.Функция ƒ(х) определена на всей оси Х.
2.При любых значениях Х функция принимает положительные значения,
т.е. лежит выше оси ОХ.
3. |
Точка (а, |
1 |
|
) – точка max. |
|
|
|
|
||||
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
||||||
2 |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||
4. |
Точки перегиба (а-σ, |
1 |
) и (а+σ, |
1 |
|
). |
||||||
|
|
|
|
|
||||||||
|
|
|
|
|
||||||||
|
2 e |
|
2 e |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
32
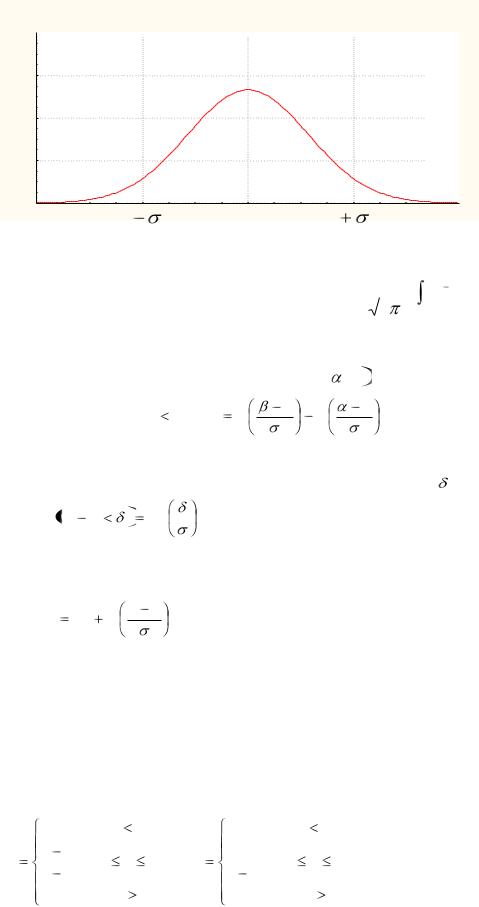
Probability Density Function
|
|
|
y=normal(x;0;1) |
|
|
|
|
0,60 |
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
0,45 |
|
|
|
|
|
|
|
0,30 |
|
|
|
|
|
|
|
0,15 |
|
|
|
|
|
|
|
0,00 |
|
|
|
|
|
|
|
-3,50 |
a |
-1,75 |
0,00 |
a |
1,75 |
X |
3,50 |
|
|
a |
|
|
|||
|
|
|
Рисунок 1.6 − Кривая Гаусса |
|
|
||
|
|
1 |
|
x |
2 |
|
|
|
|
e t |
/ 2 dt , то для |
||
|
|
|
|
|||
Если функция Лапласа задаётся формулой Ф(х) = |
|
|
|
|
||
|
|
|
|
|||
2 |
|
|||||
|
|
0 |
|
|
||
нормально распределенной случайной величины:
1) вероятность того, что непрерывная случайная величина, распределённая по нормальному закону, примет значение на интервале 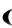 ,
, 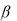 , равна
, равна
P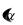 X
X 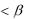
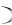 Ф a Ф a ;
Ф a Ф a ;
2) вероятность того, что отклонение нормально распределённой случайной величины по абсолютной величине меньше положительного числа , находится из
|
|
|
|
|
соотношения P |
X a |
2Ф |
|
. |
|
||||
|
|
|
|
|
3) связь между функцией распределения F(x) случайной величины Х, распределённой по нормальному закону и функцией Лапласа выражается
формулой F ( x) 0,5 Ф x a
.
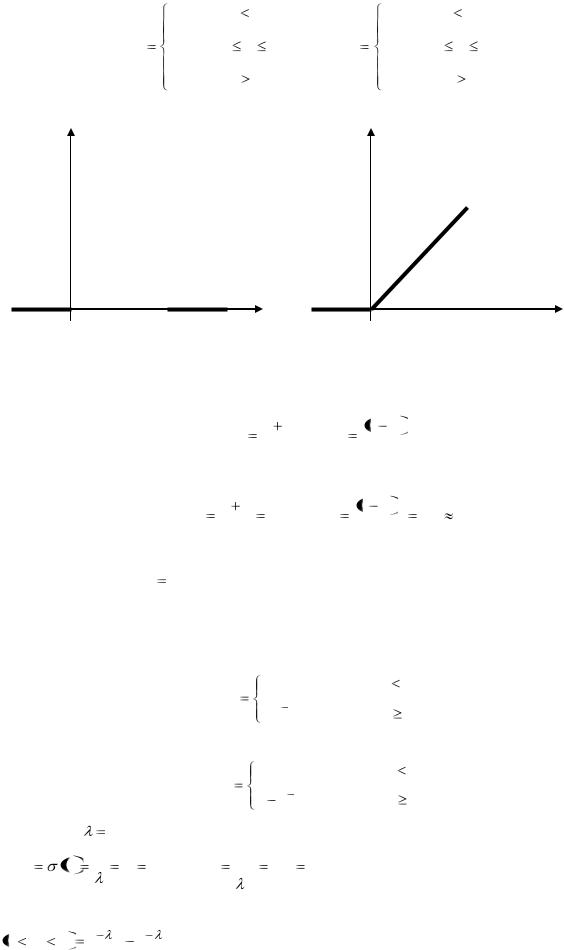
Пример 27. Поезда метро идут строго по расписанию. Интервал движения – 5 минут. Составить f(x) и F(x) случайной величины X – времени ожидания очередного поезда и построить их графики. Найти M(X), D(X).
Решение. Случайная величина X – время ожидания очередного поезда. Величина X распределена равномерно на отрезке [0,5], поэтому воспользуемся формулами
|
|
0, |
|
x |
a; |
0, |
|
|
x |
a; |
F (x) |
x |
a |
, |
a x b; f (x) |
1 |
|
, |
a x b; |
||
|
|
|
|
|||||||
|
b |
a |
|
|
|
b |
a |
|
|
|
|
|
1, |
|
x |
b; |
0, |
|
x |
b. |
|
33
|
|
0, |
|
x |
0; |
|
0, |
|
x |
0; |
|||||
Тогда имеем F (x) |
|
x |
|
, |
0 |
x 5; |
f (x) |
|
1 |
|
, |
0 |
x 5; |
||
5 |
|
5 |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
1, |
x |
5. |
|
0, |
x |
5. |
|||||||
f(x) |
|
|
|
|
|
|
F(x) |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
X |
5 X |
|
|
|
Рис. 1.7 − Графики функций F(x) и f(x) Математическое ожидание и дисперсия вычисляются по формулам:
|
M ( X ) |
b a |
; D( X ) |
|
b |
a |
2 |
. |
|
|
|||
|
|
|
|
|
|
|
|
||||||
|
2 |
|
|
12 |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
M ( X ) |
|
5 |
0 |
|
2,5; D( X ) |
5 |
0 2 |
|
25 |
2,08. |
|||
|
|
2 |
|
12 |
12 |
||||||||
|
|
|
|
|
|
|
|||||||
Пример 28. Непрерывная случайная величина распределена по показательному закону с параметром 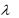 2. Составить функцию распределения, функцию плотности этой случайной величины. Найти числовые характеристики и вероятность того, что случайная величина попадет в интервал (0,3;1).
2. Составить функцию распределения, функцию плотности этой случайной величины. Найти числовые характеристики и вероятность того, что случайная величина попадет в интервал (0,3;1).
Решение. Очевидно, искомая плотность распределения
0, |
при |
x |
0; |
f (x) |
2x , при |
|
|
2e |
x |
0. |
Искомая функция распределения
0, |
при |
x |
0; |
F (x) |
2x , при |
|
|
1 e |
x |
0. |
По условию |
|
2. Следовательно, |
|
|
|
|
|
|||||||
M ( X ) |
x |
|
1 |
1 |
|
0,5; D( X ) |
1 |
|
1 |
0,25. |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
2 |
|
2 |
|
2 |
2 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Для |
нахождения |
вероятности |
|
P(0,3<X<1) |
воспользуемся |
формулой |
||||||||
P a X |
b e |
|
a |
e b . |
|
|
|
|
|
|
|
|||
34

Тогда, P 0,3 X 1 e
e 2
2 0,3
0,3 e
e 2 1
2 1 e 0,6 e 2 0,549 0,135 0,414.
e 0,6 e 2 0,549 0,135 0,414.
Пример 29. Детали, выпускаемые цехом, по размеру диаметра распределены по нормальному закону. Стандартная длина диаметра детали равна а=35, среднее квадратическое отклонение 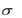 4. Требуется:
4. Требуется:
а) составить функцию плотности вероятностей; б) найти вероятность того, что диаметр наудачу взятой детали будет больше
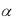 34 и меньше
34 и меньше 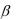 40;
40;
в) найти вероятность того, что диаметр наудачу взятой детали будет меньше 36 г) найти вероятность того, что диаметр детали отклонится от стандартной длины не
больше чем на |
2. |
Решение. а) |
Так как непрерывная случайная величина X распределена по |
нормальному закону, есть ее плотность распределения вероятностей выражается формулой
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x |
a 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x) |
|
1 |
|
|
|
|
e |
2 2 . |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Следовательно, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
x |
35 2 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
f (x) |
|
|
|
|
|
|
|
e |
|
|
|
|
32 . |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
4 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
б) Для нормально распределенной случайной величины |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
P |
|
X |
|
|
|
|
|
|
Ф |
|
|
|
|
|
a |
Ф |
|
a |
. |
|
||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P 34 |
X |
40 |
Ф |
40 |
35 |
|
Ф |
|
34 |
35 |
|
|
|
Ф 1,25 |
|
|
|
Ф 0,25 |
0,394 4 0,098 7 0,493 1. |
||||||||||||||||||
4 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
в) Вероятность того, что диаметр наудачу взятой детали будет меньше 36 |
|||||||||||||||||||||||||||||||||||||
определяется по формуле : F ( x) |
0,5 |
|
Ф |
x |
|
|
a |
; |
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
P( x |
36) |
F (36) |
0,5 |
Ф |
36 |
35 |
|
0,5 |
|
Ф(0,25) |
0,5 0,0987 |
|
0,5987 . |
||||||||||||||||||||||||
4 |
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
г) Последнее задание решаем по формуле P |
X |
|
|
|
a |
|
|
|
2Ф |
|
. |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
Таким образом, |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
P |
X |
35 |
|
2 |
|
2Ф |
|
|
2Ф 0,5 |
0,3829 , |
|
|
|
|
|||||||||||||||||||||||
|
|
4 |
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где Ф(x) – интегральная функция Лапласа (Приложение Б). |
|
||||||||||||||||||||||||||||||||||||
35

Тема 11. Закон больших чисел
Под законом больших чисел в узком смысле понимается ряд математических теорем, в каждой из которых для тех или иных условий устанавливается факт приближения средних характеристик большого числа испытаний к некоторым определенным постоянным.
Неравенства Маркова и Чебышева
Неравенство Маркова. Пусть случайная величина X принимает только неотрицательные значения и имеет конечное математическое ожидание M(X). Тогда для любого δ>0 имеют место неравенства Маркова:
P( X 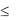 ) 1 M ( X ) , P( X
) 1 M ( X ) , P( X 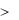 ) M ( X ) .
) M ( X ) .
Пример 30. Вероятность того, что у отдельного вкладчика некоторого сберегательного банка сумма вклада не больше 3 млн руб., превышает 0,8. Банк
обслуживает |
1 |
000 |
вкладчиков. |
Какова |
общая сумма вкладов этого |
||||||||||||
сберегательного банка? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. P( X |
3) |
0,8 1 |
|
M ( X ) |
|
. Тогда |
M ( X ) |
|
0,2 |
M ( X ) |
0,6 . |
|
|||||
3 |
|
3 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Общая сумма 600 000 000 руб. |
|
|
|
|
|
|
|
|
|
|
|
||||||
Неравенство Чебышева. Для любого ε>0 и любой случайной величины X, |
|||||||||||||||||
дисперсия которой конечна, выполняются неравенства |
|
|
|
|
|||||||||||||
|
|
|
|
D( X ) |
|
, P( |
|
|
|
D( X ) |
. |
||||||
|
P( |
X M ( X ) |
) |
X M ( X ) |
) 1 |
||||||||||||
|
2 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 31. Вероятность того, что студент учебного заведения в период работы читального зала посетит его, равна 0,3. Оценить вероятность того, что среди 900 студентов читального зала посетят от 240 до 300 человек.
Решение. M(X) = np = 900 · 0,3 = 270; D(X) = npq = 189.
Величина отклонения от M(X) равна 240 270
 300 270 30
300 270 30 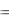 .
.
Тогда P( |
|
X 270 |
|
30) 1 |
189 |
0,79 . |
|
|
|
||||||
|
|
|
|
||||
|
|
900 |
|||||
|
|
|
|
|
|
||
Закон больших чисел в форме Чебышева
Теорема (непредельная форма). Пусть X1 , X 2 , …, X n  последовательность попарно независимых, однородных случайных величин, имеющих конечные
последовательность попарно независимых, однородных случайных величин, имеющих конечные
дисперсии |
D( X1 ), D( X 2 ), …, D( X n ), ограниченные сверху числом С ( |
||
|
|
|
|
D(Xi ) C(i |
1, n) ). Тогда для любого сколь угодно малого числа ε>0, имеют место |
||
неравенства |
|
|
|
36

|
|
|
|
|
|
|
|
|
|
|
|
C |
, P( |
|
|
|
|
|
|
|
|
|
|
|
|
C |
. |
|
P( |
X M ( X ) |
) 1 |
|
X M ( X ) |
) |
|||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
n 2 |
|
|
X 2 , …, |
|
|
|
|
|
n 2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
X1 , |
|
|
|
|
|||||||||||
Теорема (предельная форма). Пусть |
X n |
последовательность |
|||||||||||||||||||||||||
независимых, однородных случайных величин, имеющих конечные D(X), которые |
|||||||||||||||||||||||||||
ограничены сверху постоянной С. Тогда при n |
|
|
и любого сколь угодно малого |
||||||||||||||||||||||||
числа |
0имеют место предельные равенства: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
1; |
|
|
|
|
|
|
|
0 . |
||||||||||||
|
lim P |
X M X |
|
lim |
P |
X M X |
|
||||||||||||||||||||
|
n |
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Закон больших чисел в форме Бернулли
Теорема (непредельная форма). Если проводится n повторных независимых испытаний, в каждом из которых вероятность появления событий A постоянна и равна p, то при n 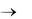 , и для любого сколь угодно малого числа
, и для любого сколь угодно малого числа 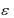 0 , имеют место неравенства:
0 , имеют место неравенства:
|
|
|
|
|
|
|
pq |
; P( |
|
|
|
|
pq |
, |
|
|
||
|
|
P( |
W p |
) 1 |
W p |
) |
|
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
m |
|
|
|
|
|
|
|
n 2 |
|
|
|
|
|
n 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
где W |
относительная частота появления события А. |
|
|
|
|
|||||||||||||
|
|
|
|
|
||||||||||||||
n |
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Теорема (предельная форма). Если в условиях теоремы Бернулли n |
, то для |
|||||||||||||||||
любого сколь угодно малого числа |
0 , справедливы предельные соотношения |
|
||||||||||||||||
|
|
|
|
|
1; |
|
|
|
0 . |
|
|
|||||||
|
|
lim P |
W |
p |
|
lim P |
W p |
|
|
|
||||||||
|
|
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
|||
Центральная предельная теорема в форме Ляпунова |
|
|
|
|
||||||||||||||
Теорема. Пусть X1 , X 2 , …, X n |
независимые случайные величины, имеющие |
|||||||||||||||||
один и тот же закон распределения с |
M ( X i ) |
a и D( X i ) |
2 . Тогда при n |
, |
||||||||||||||
закон распределения суммы X |
X1 |
X 2 |
... |
X n неограниченно приближается и |
||||||||||||||
нормальному. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Раздел 2 . Элементы математической статистики
Тема 12. Первоначальные понятия математической статистики
Проведение экономических исследований связано с изучением свойств различных совокупностей однотипных объектов (людей, предприятий, товаров и т.п.). При этом каждый объект, входящий в состав совокупности, характеризуется
37
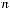
некоторым числом хi — величиной изучаемого признака X. Для обозначения таких совокупностей вводится понятие генеральной совокупности.
Под генеральной совокупностью понимается вся совокупность однотипных объектов, которые изучаются в данном исследовании. Примером генеральной совокупности может служить совокупность работников данной отрасли, а признаком Х, например, годовой доход работника. Однако на практике в большинстве случаев мы имеем дело только с частью возможных наблюдений, взятых из генеральной совокупности.
Выборка (выборочная совокупность) — это совокупность случайно отобранных объектов, составляющих лишь часть генеральной совокупности.
Объёмом совокупности (выборочной или генеральной) называют число объектов данной совокупности.
Например, из 1 000 изделий отобрано для обследования 100 изделий, объем генеральной совокупности N=1 000, а объём выборки n=100.
Наблюдаемые значения хi признака Х называют вариантами . Если расположить варианты в порядке возрастания получим дискретный вариационный ряд.
Под частотой ni значения признака понимают число членов совокупности с данной вариантой. Отношение частоты к объему совокупности называют
относительной частотой значения признака: wi = 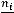 .
.
Статистическим распределением выборки называют перечень вариант xi и
соответствующих им частот ni или относительных частот wi (причем сумма всех частот равна объёму выборки, а сумма всех относительных частот равна 1).
xi |
|
x1 |
|
x2 |
|
…. |
|
xk |
ni |
|
n1 |
|
n2 |
|
…. |
|
nk |
|
|
|
|
или |
|
|
|
|
xi |
|
x1 |
|
x2 |
|
…. |
|
xk |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
wi |
|
w1 |
|
w2 |
|
…. |
|
wk |
Вариационный ряд, заданный в таком виде, называют дискретным. Графическим представлением статистического распределения может служить
полигон частот ( или относительных частот) .
38

Полигоном частот называют ломаную , отрезки которой соединяют точки (хi,
ni).
Полигоном относительных частот называют ломаную , отрезки которой соединяют точки (хi, wi).
Непрерывное статистическое распределение выборки можно получить, разбив весь интервал, в котором заключены все значения признака, на k частичных интервалов длины h. Согласно формуле Стерджеса число частичных интервалов определяется по формуле 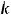

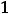
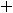
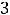
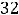
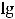
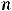 , а величина интервала
, а величина интервала 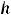

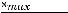
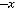
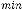 .
.
Для каждого частичного интервала ставится в соответствие ni - сумма частот вариант, попавших в данный частичный интервал.
Графическим представлением непрерывного статистического распределения может служить гистограмма частот ( или относительных частот) .
Гистограммой частот называется ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 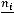
Гистограммой относительных частот называют ступенчатую фигуру,
состоящую из прямоугольников, основаниями которых служат частичные интервалы длины h, а высоты равны отношению 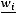 .
.
Пример 32. Из большой группы предприятий одной из отраслей промышленности случайным образом отобрано 30, по которым получены значения стоимости основных фондов в млн руб.:
3; 4; 2; 3; 3; 6; 5; 2; 4; 7; 5; 5; 3; 4; 3; 2; 6; 7; 5; 4; 3; 4; 5; 7; 6; 2; 3; 6; 6; 4.
Составить дискретное статистическое распределение выборки, записать распределение относительных частот, построить полигон частот.
Решение. Различные значения признака запишем в порядке возрастания и под каждым из них запишем соответствующие частоты. Получим дискретное
статистическое распределение выборки: |
|
|
|
|
|||
|
xi |
|
3 |
4 |
5 |
6 |
7 |
|
2 |
||||||
|
|
|
|
|
|
|
|
|
ni |
4 |
7 |
6 |
5 |
5 |
3 |
|
|
|
|
|
|
|
|
Проверка: сумма всех частот должна быть равна объёму выборки: n=4+7+6+5+5+3=30.
39
Найдем относительные частоты, для чего разделим частоты на объём выборки
|
w1 |
4 |
|
|
0,13; |
w2 |
7 |
|
|
0,23 ; |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
30 |
|
|
30 |
||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
w3 |
6 |
|
|
0,2 ; |
|
w4 |
5 |
|
|
0,17 ; |
||||
|
|
|
|
|
|
|
|
|
|
|
|||||
30 |
|
|
30 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|||||||
|
w5 |
5 |
|
|
0,17 ; |
w6 |
3 |
|
|
0,1. |
|||||
|
|
|
|
|
|
|
|
|
|
||||||
30 |
30 |
|
|||||||||||||
|
|
|
|
|
|
|
|
||||||||
Напишем распределение относительных частот: |
|||||||||||||||
|
|
|
|
|
|
|
|
||||||||
xi |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|||||||
wi |
0,13 0,23 0,2 0,17 0,17 0,1 |
|
|||||||||||||
Контроль: |
wi |
0,13 |
0,23 |
0,2 0,17 0,17 0,1 1. |
|||||||||||
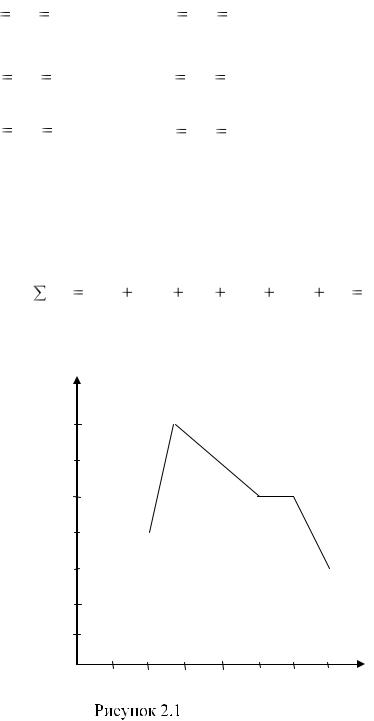
Строим полигон частот. Для этого строим точки с координатами (xi;ni):
(2;4), (3;7), (4;6), (5;5), (6;5), (7;3) и соединяем их последовательно отрезками.
ni
7
6
5
4
3
2
1
1 |
2 |
3 |
4 |
5 |
6 |
7 |
xi |
полигон частот
Пример 33. Выборочно обследовано 26 предприятий лёгкой промышленности по объему валовой продукции. Получены следующие результаты в млн руб.:
15,0; 16,4; 17,8; 18,0; 18,4; 19,2; 19,8; 20,2; 20,6; 20,6; 20,6; 21,3; 21,4; 21,7; 22,0; 22,2; 22,3; 22,7; 23,0; 24,2; 24,2; 25,1; 25,3; 26,0; 26,5; 27,1.
40
