
5126
.pdf
31
Рис. 21.
На рис. 21 показано окно Solution list – список решения задачи. В данном окне указан перечень всех переменных при решении данной задачи, тип переменной (базисная или свободная) и их значения.
Решение исходной задачи выпишем из строки Solution рис. 19:
Х =(14,2857; 96,4286; 0; 0); Zmax =1 178,571.
Предприятие получит максимальную прибыль в размере 1 178,571 у.д.е., если будет выпускать первую продукцию в объеме 14,285 7 ед. и вторую продукцию в объеме 96,428 6 ед. и откажется от производства третьей и четвертой продукции (х3=0, х4=0).
5.Двойственность в линейном программировании
5.1.Составление двойственной задачи
Скаждой задачей линейного программирования тесно связана другая линейная задача, называемая двойственной. Первоначальная задача называется исходной. Решение одной из задач может быть получено непосредственно из решения другой.
|
|
Исходная задача |
|
|
Двойственная задача |
|
|
|||||||||||
|
n |
|
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
Z |
с j |
х j max |
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
W |
bi |
yi min |
|
|
|||||||||||
|
j |
1 |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
|
|
(1) |
|
m |
|
|
|
|
|
|
(2) |
|
|
aij |
x j |
bi , (i 1, m) |
|
|
|
|
|
|
|
|
|
||||||
|
|
aij |
yi |
c j , ( j 1, n) |
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
j 1 |
|
|
|
|
|
|
|
|
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
yi |
0, (i |
1, m) |
|
|
||||
|
x j |
0, ( j |
1, n) |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Переменные |
двойственной |
задачи |
yi |
называют объективно |
||||||||||||||
обусловленными оценками, или двойственными оценками.
Правила построения двойственной задачи по отношению к исходной:
1. В исходной задаче ищется максимум целевой функции, а в двойственной – минимум. При этом в исходной задаче максимизации все ограничения вида , а в двойственной задаче минимизации их необходимо заменить на противоположные .
2. Число ограничений одной задачи равно числу переменных другой задачи и наоборот.

32
3. Матрицы коэффициентов при переменных в системах ограничений обеих задач транспонированы относительно друг друга. Следовательно, столбец коэффициентов в ограничениях исходной задачи записывается как строка коэффициентов в ограничениях двойственной задачи и наоборот.
4.Коэффициенты целевой функции исходной задачи являются свободными членами ограничений двойственной задачи. Свободные члены ограничений исходной задачи становятся коэффициентами целевой функции двойственной задачи.
5.Все переменные хj и yi обеих задач неотрицательны.
Задачи (1–2) называются симметричными взаимно двойственными задачами.
Пример 1. Составим двойственную задачу к исходной.
Z 6x1 x2 max
x1 |
3x2 |
10 / y1; |
4x1 |
6x2 |
7 / y2; |
x1 |
x2 |
3/ y3; |
x1 |
0, x2 |
0. |
Двойственная задача имеет следующий вид:
W=10y1+7y2+3y3→min y1 4 y2 y3 6,
3y1 |
6 y2 y3 |
1, |
||
|
|
|
|
|
y1 |
0 (i 1, 3). |
|
||
5.2. Теоремы двойственности и свойства двойственных оценок
Первая (основная) теорема двойственности
Если одна из двойственных задач имеет оптимальное решение Х , то и
вторая имеет оптимальное решение Y , причем экстремальные значения их целевых функций совпадают:
n |
|
|
х * |
|
m |
Z ( Х ) |
c |
j |
W (Y ) |
b y . |
|
|
|
j |
|
i i |
|
j |
1 |
|
|
|
i 1 |
Экономически это означает, что план производства Х  и набор оценок
и набор оценок
ресурсов Y  являются оптимальными только тогда, когда цена выпускаемой продукции и суммарная оценка ресурсов совпадают.
являются оптимальными только тогда, когда цена выпускаемой продукции и суммарная оценка ресурсов совпадают.
Вторая теорема (о равновесии)
В оптимальном плане для каждой пары сопряженных условий исходной и двойственной задач выполняются соотношения: если одно из них выполняется как строгое равенство, то другое как строгое неравенство,

33
и наоборот,
еслиx*j |
|
|
m |
|
yi* |
|
|
0, то |
aij |
c j ; |
|||||
|
|
|
j |
1 |
|
|
|
если x* |
|
|
m |
|
y* >сj; |
|
|
0, то |
a |
ij |
|
||||
j |
|
|
|
|
i |
|
|
|
|
|
i |
1 |
|
|
|
n |
|
|
x* |
b , то y* |
|
||
если |
a |
ij |
>0; |
||||
|
|
j |
|
i |
i |
|
|
j |
1 |
|
|
|
|
|
|
если n aij  x*j <bi, то yi*=0.
x*j <bi, то yi*=0.
j 1
(5.1)
(5.2)
(5.3)
(5.4)
Теперь сформулируем двойственную задачу.
Пусть некоторая организация решила закупить все ресурсы рассматриваемого предприятия. При этом необходимо установить оптимальную цену на приобретаемые ресурсы yi исходя из следующих условий:
-покупающая организация старается минимизировать общую стоимость ресурсов;
-за каждый вид ресурсов надо заплатить не менее той суммы, которую хозяйство может выручить при переработке сырья в готовую продукцию.
Из изложенных выше теорем двойственности вытекают свойства двойственных оценок.
Свойство 1. Оценка как мера дефицитности ресурсов.
Из условия (5.3–5.4) следует, если оценка yi единицы ресурса i-го вида положительна (yi*>0), то при оптимальном плане этот ресурс используется полностью; если же ресурс используется не полностью, то его оценка равна нулю (yi*=0). В первом случае увеличение объема i-го ресурса приведет к увеличению выпуска продукции. Такой ресурс будем называть дефицитным. Во втором случае увеличение объёма i-го ресурса не внесет никакого вклада в результат производства. Такой ресурс будем называть недефицитным.
Величина, на которую увеличивается значение целевой функции при увеличении объема дефицитного ресурса на единицу, называется оценкой ресурса, или его теневой ценой.
Свойство 2. Оценка как мера влияния ограничения на оптимальное
значение целевой функции. Величина оценки единицы i-го вида ресурса (yi*) показывает, насколько изменится стоимость всей произведенной продукции в оптимальном плане, если i-й ресурс изменить на единицу.
Z yi |
bi , |
(5.5) |
где yi – двойственная оценка i-го ресурса; |
bi – приращение i-го ресурса; |
|
Z – изменение целевой функции. |
|
|
Используя выражение (5.5), |
мы можем выявить направление |
|

34
деятельности предприятия по устранению «узких» мест, обеспечивающее наибольшее изменение целевой функции, при условии, что значения переменных yi в оптимальном плане остаются неизменными.
Свойство 3. Оценка как инструмент определения эффективности выпускаемой продукции. Из условия (5.1–5.2) следует, что если хj*>0, то j-й вид продукции выпускается в оптимальном плане, т.е. эта продукция не убыточная, поскольку оценка ресурсов на производство единицы j-й продукции равна стоимости единицы этой продукции. Такую продукцию будем называть рентабельной. Если же xj*=0, то j-й вид продукции убыточен, он не будет выпускаться в оптимальном плане, поскольку аналогичная оценка ресурсов превышает цену единицы этой продукции. Данную продукцию будем называть нерентабельной.
Свойство 4. Оценка как инструмент балансировки суммарных затрат и результатов.
В оптимальном плане результаты производства совпадают с оценкой затрат на производство:
n |
|
m |
Z max |
с j х j W min |
bi yi . |
j 1 |
|
i 1 |
5.3. Анализ решения двойственной задачи
Для приведенной в теме 4.2. модели исходной задачи составим модель двойственной задачи.
Общая стоимость ресурсов выразится величиной
(5.6)
при условиях, что стоимость всех ресурсов, расходуемых на производство единицы j-го вида продукции должна быть не менее цены соответствующей продукции
4 y1 |
y2 |
2 y3 |
15, |
|
2 y1 |
4 y2 |
y3 |
10, |
|
3y1 |
5 y2 |
4 y3 |
8, |
(5.7) |
|
||||
2 y1 |
7 y2 |
6 y3 |
12, |
|
yi 0(i 1,3).
Двойственная задача в основной форме имеет вид:
4 y1 |
y2 |
2 y3 |
l1 |
15, |
|
|
|||
2 y1 |
4 y2 |
y3 |
|
|
l2 |
10, |
|
||
3y1 |
5 y2 |
4 y3 |
|
|
|
l3 |
8, |
|
|
2 y1 |
7 y2 |
6 y3 |
|
|
|
|
l4 |
12, |
|
|
|
|
|
|
|
|
|
|
|
yi |
0,l j |
0(i |
1,3, j |
1, 4). |
|||||
W |
250 y1 |
400 y2 |
|
450 y3 |
min |
||||
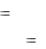
35
Здесь lj есть превышение затрат на выпуск единицы j-го вида продукции над ценой.
Вернемся к п. 4.3. – анализ решения задачи с помощью ППП QM for Windows. В нижней части отчета Ranging (рис.6 темы 4.3) указаны границы устойчивости переменных двойственной задачи. В столбце Dual Value указаны значения двойственных оценок ресурсов в оптимальном плане (yi*). В столбце Slack – остатки i-х ресурсов (Si). В столбце Original Value - исходные значения запасов ресурсов. В последних двух столбцах отражены границы изменения запасов. Lower Bound – нижний предел устойчивости для запасов, Upper Bound – верхний предел устойчивости для запасов.
Решение двойственной задачи выпишем из столбца Dual:
Y  (3,5714; 0,7143; 0);
(3,5714; 0,7143; 0);
W min 1178,571.
При таком производстве будут полностью израсходованы первый и второй ресурсы (их остатки S1=S2=0), неиспользованными останутся 325 ед. третьего ресурса.
Исследуем решение исходной и двойственной задачи по свойствам двойственных оценок.
Дефицитный ресурс, полностью используемый по оптимальному плану производства выпуска продукции, имеет положительную оценку, а недефицитный ресурс, не полностью используемый, имеет нулевую оценку. Первый и второй ресурс являются дефицитными, их оценки соответственно равны у1*=3,5714 и у2*=0,7143. Третий ресурс является недефицитным, его оценка у3*=0.
Если ограничения исходной задачи подставить полученные значения хj*, то получим:
4·14,2857+2·96,4286+3·0+2·0=250=250; 14,2857+4·96,4286+5·0+7·0=400=400; 2·14,2857+96,4286+4·0+6·0=125<450.
Остаток третьего ресурса S3=450-125=325.
Исходя из второго свойства, двойственная оценка ресурса показывает, насколько изменится значение целевой функции, если i-й ресурс изменить на единицу, при условии, что это изменение не выйдет за границы устойчивости двойственных оценок. В нашем случае дополнительное приобретение третьего ресурса даст нулевой вклад в целевую функцию, т.к. этот ресурс является недефицитным из-за невозможности его полного использования в оптимальном плане. Так как суммарный расход недефицитного ресурса меньше его запасов на предприятии, то план производства им не лимитируется. Такой ресурс не препятствует и дальше увеличивать целевую функцию.
Дополнительное приобретение дефицитных ресурсов расширяет

36
производство и приводит к увеличению прибыли. Дополнительная единица первого и второго ресурса приведет к увеличению прибыли соответственно на 3,571 4 и 0,714 3 у.д.е. Больший вклад в результат производства даст первый ресурс, т.к. его оценка больше.
Согласно свойству третьему, рентабельной является первая и вторая продукция, т.к. она выпускается в оптимальном плане в объемах соответственно 14,285 у.д.е. и 96,428 6 у.д.е. Для данной продукции нет превышения затрат над ценой (l1=l2=0). От производства продукции третьего и четвертого вида предприятию необходимо отказаться, т.к. она не выпускается в оптимальном плане. У данных видов продукции идет превышение затрат над ценой за единицу продукции соответственно на 6,285 7 и 0,142 9 у.д.е. Эта продукция является нерентабельной, и ее производство для предприятия убыточно.
Если в ограничения двойственной задачи подставить полученные значения yi*, то получим
4·3,571 4+0,714 3·0=14,999 9 15; 2·3,571 4+4·0,714 3+0=10=10;
3·3,571 4+5·0,714 3+4·0=14,285 7>8; 2·3,571 4+7·0,714 3+6·0=12,142 9>12,
т.е. превышение затрат над ценой для третьего вида продукции составляет l3=14,285 7–8=6,285 7 у.д.е., а для четвертого вида продукции l4=12,142 9–12=0,142 9 у.д.е. Для включения в план данных видов продукции предприятие должно либо поднимать цены, либо снижать затраты.
Для проверки четвертого свойства вычислим значении целевых функций исходной и двойственной задач.
Z=15·14,285 7+10·96,428 6+8·0+12·0=1 178,571;
W=250·3,571 4+400·0,714 3+450·0=1 178,57,
т.е. в оптимальном плане результаты производства балансируются затратами системы на это производство.
Варианты заданий для выполнения работы
При известных нормах затрат ресурсов на производство единицы продукции, запасах ресурсов, ценах на продукцию определить план выпуска продукции, обеспечивающий получение максимальной прибыли от реализации продукции. Для этого:
составить модель исходной и двойственной задачи; решить задачу, используя ППП QM for Windows;
исследовать полученные оптимальные решения по свойствам двойственных оценок.
37
Варианты запасов ресурсов
№ |
|
|
|
|
Номер варианта запаса ресурсов |
|
|
|
|||||
ресур- |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
са |
1,13 |
2,14 |
3,15 |
4,16 |
|
5,17 |
6,18 |
7,19 |
8,20 |
9,21 |
10,22 |
11,23 |
12,24 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
330 |
720 |
280 |
690 |
|
750 |
440 |
670 |
310 |
550 |
310 |
440 |
730 |
2 |
570 |
430 |
750 |
350 |
|
600 |
260 |
380 |
680 |
300 |
700 |
600 |
360 |
3 |
400 |
550 |
350 |
220 |
|
450 |
800 |
420 |
500 |
700 |
300 |
800 |
520 |
Варианты цен
№ вида |
|
|
|
|
|
Варианты цен |
|
|
|
|
|
||
продукции |
1,13 |
2,14 |
3,15 |
4,16 |
5,17 |
6,18 |
7,19 |
|
8,20 |
9,21 |
10,22 |
11,23 |
12,24 |
1 |
5 |
4 |
8 |
3 |
7 |
5 |
4 |
|
4 |
7 |
5 |
8 |
8 |
2 |
3 |
8 |
3 |
3 |
6 |
5 |
2 |
|
2 |
7 |
4 |
3 |
3 |
3 |
7 |
1 |
7 |
4 |
8 |
3 |
7 |
|
2 |
9 |
8 |
5 |
2 |
4 |
2 |
6 |
6 |
8 |
2 |
4 |
5 |
|
5 |
8 |
3 |
5 |
1 |
Нормы расхода ресурсов на производство единицы продукции
Вид |
|
|
|
|
Вариант |
|
|
|
|
ресурса |
1,13 |
2,14 |
3,15 |
|
4,16 |
|
5,17 |
6,18 |
7,19 |
|
|
|
|
Вид продукции |
|
|
|
||
|
|
|
|
|
|
|
|
1 2 3 4 |
1 2 3 4 |
1 |
4 2 1 6 |
3 6 8 5 |
2 4 3 6 |
|
6 2 3 7 |
|
3 5 0 1 |
3 2 3 0 |
3 5 1 4 |
2 |
3 5 3 4 |
2 1 2 3 |
3 2 2 3 |
|
2 4 2 1 |
|
4 6 3 7 |
8 2 1 7 |
2 6 4 3 |
3 |
8 1 6 5 |
4 5 7 2 |
4 6 3 5 |
|
5 4 0 7 |
|
1 3 3 2 |
5 4 2 2 |
3 1 3 8 |
Окончание таблицы
Вид ресурса |
|
|
Вариант |
|
|
|
8,20 |
9,21 |
10,22 |
11,23 |
12,24 |
|
|
|
Вид продукции |
|
|
|
1 2 3 4 |
1 2 3 4 |
1 2 3 4 |
1 2 3 4 |
1 2 3 4 |
1 |
2 6 4 3 |
1 4 5 0 |
0 4 4 1 |
2 4 3 8 |
1 2 3 7 |
2 |
3 1 4 7 |
6 2 8 4 |
2 5 5 2 |
0 6 3 2 |
5 2 4 6 |
3 |
5 4 0 2 |
5 3 4 7 |
2 6 3 4 |
7 5 1 7 |
8 1 4 2 |
6. Транспортная задача
Это задача о наиболее экономном плане перевозок однородного или взаимозаменяемого продукта из пунктов производства в пункты потребления.
6.1.Постановка и модель транспортной задачи
Вm пунктах отправления А1, А2, …, Аm (поставщики) сосредоточено некоторое количество единиц однородного груза а1, а2, …, аm. Данный груз следует перевезти в n пунктов назначения В1, В2, … , Вn (потребители), спрос в которых соответственно составляет b1, b2, …, bn единиц этого груза. Заданы расходы Сij на перевозку единицы груза из пункта Аi в пункт Вj. Требуется рассчитать оптимальный план перевозок, т.е. определить, сколько груза должно быть отправлено от i-го поставщика j-
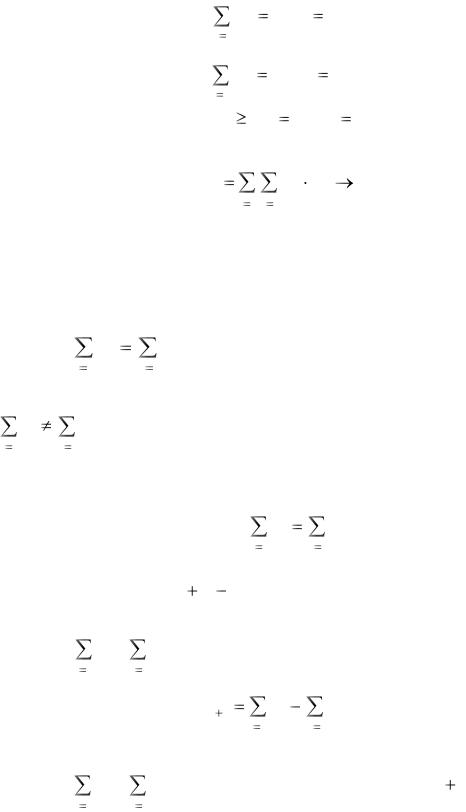
38
му потребителю с минимальными транспортными издержками. Построим математическую модель задачи.
Обозначим объем перевозки груза из пункта Аi в пункт Вj тогда
|
n |
|
|
|
|
|
|
|
|
|
хij |
ai , (i 1, m); |
|||||||
j |
1 |
|
|
|
|
|
|
|
|
m |
|
|
|
|
|
|
|
|
|
|
хij |
b j , ( j 1, n); |
|||||||
i |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
хij |
0 (i 1, m, j 1, n). |
||||||||
Общая стоимость всех перевозок составит:
m |
n |
|
Z |
сij хij |
min . |
i 1 j |
1 |
|
через Хij,
(6.1)
(6.2)
(6.3)
(6.4)
Она должна быть минимизирована.
Первое условие означает, что вся продукция вывозится от поставщиков; второе условие означает, что спрос потребителей должен быть удовлетворен. Должно выполняться условие неотрицательности (6.3).
Различают задачи с закрытой моделью, т.е. когда выполняется условие
m |
n |
|
баланса |
ai |
b j , и открытой моделью, т.е. когда баланс между |
i |
1 |
j 1 |
запасами грузов у поставщиков и потребностями потребителей отсутствует
m |
n |
ai |
b j . |
i 1 |
j 1 |
Необходимым и достаточным условием разрешимости транспортной задачи выполнение условия баланса:
m |
n |
ai |
b j . |
i 1 |
j 1 |
В этом случае она имеет оптимальный план, и число базисных
|
|
|
|
|
|
|
|
|
|
|
|
|
неизвестных равно m n 1, |
где |
m - число поставщиков, n – число |
||||||||||
потребителей. |
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
n |
|
|
|
|
|
|
|
|
|
Если |
ai |
> |
|
b j , |
то вводится дополнительно (n+1)-й потребитель с |
|||||||
i |
1 |
|
j |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
m |
|
n |
|
||
объемом |
потребления |
Bn 1 |
ai |
|
b j . Стоимость |
перевозок Сi, n+1 |
||||||
|
|
|
|
|
|
i |
1 |
|
j 1 |
|
||
дополнительного столбца принимается равным нулю. |
|
|||||||||||
m |
|
n |
|
|
|
|
|
|
|
|
|
|
Если |
ai |
< |
|
b j , |
то дополнительно вводится (m |
1) -й поставщик с |
||||||
i |
1 |
|
j |
1 |
|
|
|
|
|
|
|
|
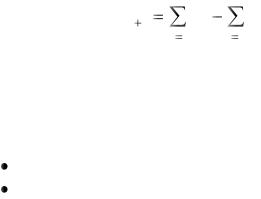
|
|
39 |
|
n |
m |
запасами груза am 1 |
b j |
ai . Все показатели Cm+n, j этой строки |
j |
1 |
i 1 |
также принимаются равными нулю.
Процедура решения транспортной задачи производится в специальных (распределительных) таблицах. В транспортной таблице занятые клетки соответствуют базисным неизвестным, а пустые клетки – свободным.
Решение транспортной задачи условно происходит в два этапа: построение начального допустимого плана; проверка его на оптимального (улучшение опорного плана).
6.2. Построение начального допустимого плана
Существует несколько методов построения начального допустимого плана: метод северо-западного угла и метод наименьшей стоимости.
Диагональный метод или метод серо-западного угла. При этом методе на каждой итерации построения первого опорного плана заполняется верхняя левая клетка (северо-западный угол) оставшейся части таблицы. При этом методе заполнение таблицы начинается с клетки переменной Х11 и заканчивается в клетке неизвестной Xmin, т.е. идет как бы по диагонали таблицы перевозок.
Недостатком данного метода является то, что он не учитывает транспортные затраты Сij, в результате чего полученный или начальный опорный план может быть достаточно далек от оптимального.
Метод наименьшей стоимости учитывает затраты на перевозку Сij. При построении исходного плана этим методом выбирают в таблице клетку с наименьшей стоимостью, если таких клеток несколько, выбирают любую, записывают в эту клетку максимально возможную поставку, исключая один из пунктов Ai или Bj. Если исключают оба пункта одновременно, то в рядом стоящую клетку записывают ноль. Продолжают распределять груз, переходя в клетки с большей стоимостью.
6.3. Метод потенциалов
Получив первый опорный план, следует проверить его оптимальность и, если требуется, перейти к новому опорному плану с лучшим значением целевой функции. Для этого используют метод потенциалов.
Теорема о потенциалах. Если X*=(Xij*) является оптимальным планом транспортной задачи, то ему соответствует система из m+n чисел Ui* и V*j, которые удовлетворяют условиям
Ui*+Vj*=Cij, для Xij*>0 (базисных); Ui*+Vj*<Cij, для Xij*=0 (свободных).

40
Алгоритм метода потенциалов
1.Составляем начальный план перевозок.
2.Строим систему потенциалов на основе условия
Ui+Vj=Cij.
Числа Ui и Vj называются потенциалами соответственно поставщиков и потребителей. Поскольку число потенциалов (m+n) всегда на единицу больше числа уравнений ( m n 1) , то выбираем строку, где есть занятая
клетка и для этой строки берем потенциал равным нулю, например U1=0. Остальные потенциалы находим из условия.
3. Затем для всех свободных клеток определяем характеристики
Eij=Cij-(Ui+Vj).
Характеристика клетки показывает, насколько изменится целевая функция, если в соответствующую клетку сделать поставку равную единице.
Если все свободные неизвестные Eij>0, то получим оптимальный план перевозок. Если среди характеристик есть Eij=0, то план оптимальный, но не единственный, если же встречаем Eij<0, то план не оптимален и его надо улучшить.
Характеристики записывают в левом нижнем углу свободных клеток транспортной таблицы.
1. Для улучшения плана выберем клетку с наименьшей отрицательной характеристикой и построим для нее замкнутую линию (контур), начальная вершина которой лежит в выбранной клетке, а все остальные – в занятых клетках, число вершин всегда четное. Контур состоит из горизонтальных и вертикальных отрезков прямых. Для каждой свободной клетки можно построить только один контур. В вершинах контура расставляем поочередно знаки «+» и « - », начиная с клетки, для которой контур строится.
Наиболее часто контур имеет вид прямоугольника, но возможны и другие разновидности.
Величина поставки, которую необходимо перераспределить по контуру, определяется как наименьшая из поставок в вершинах контура со знаком « - », и на эту величину увеличиваются поставки в положительных вершинах и уменьшаются в отрицательных вершинах. При этом освобождается только одна клетка, а клетка, для которой контур строится, заполняется.
Далее строим новую таблицу перевозок и проверяем оптимальность плана.
