
5126
.pdf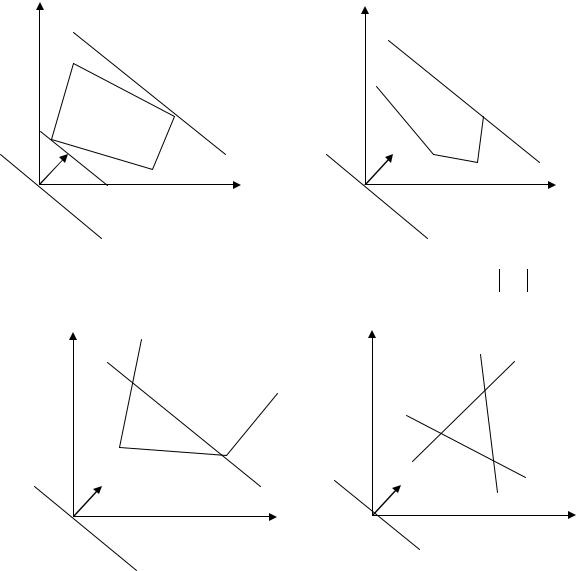
21
5.Если при перемещении линии уровня по области допустимых решений она уходит в бесконечность, то задача не имеет решения ввиду неограниченности целевой функции.
6.Если задача линейного программирования имеет оптимальное решение, то, чтобы найти компоненты решения, достаточно решить систему из двух уравнений, определяющих вершину, в которой достигается оптимальное значение.
7.Если целевая функция достигает экстремума в нескольких крайних точках, то задача имеет бесконечное множество решений. Оптимальным решением является любая выпуклая линейная комбинация этих крайних точек (альтернативный оптимум).
8.После нахождения оптимальных решений необходимо вычислить значение целевой функции Z на этих решениях. На рис. 9–12 изображены различные ситуации нахождения оптимального решения.
Х2
|
|
|
В |
|
|
|
|
|
С |
|
A |
Z max |
||
|
|
|
|
|
|
|
|
=(C1, C2) Z min D |
|
О |
n |
|
||
|
|
|
Х1 |
|
|
|
|
|
|
Z=0
Рис. 9. Максимум достигается в точке С, а минимум – в точке А.
Х2
Z max=+∞
Х2
А
Е
|
|
|
В |
|
|
|
Z max |
|
|
D |
С |
|
n =(C1, C2) |
||
|
|
||
О |
|
|
Х1 |
Z=0
Рис. 10. Максимум функции Z достигается в любой точке АВ
Х2
|
|
|
|
|
|
n |
|
|
n |
|
|
|
|
||||
О |
|
Х1 |
О |
|
||||
|
|
|
|
|
|
Z=0 |
Х1 |
|
|
|
|
Z=0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
Рис. 12. Область допустимых Рис. 11. Максимум функции Z не решений – пустая область достижим

22
Пример 1. Решить графическим методом следующую задачу линейного программирования:
Z=2x1+x2→max,
2х1 |
х2 |
14, |
х1 |
3х2 |
15, |
х1 |
|
16, |
|
х2 |
4, |
х1 |
0, х2 |
0. |
Решение. Строим область допустимых решений задачи. Для этого последовательно определяем области решений каждого неравенства. Вместо неравенств 2х1+х2 14 рассмотрим прямую 2х1+х2=14. Изобразим ее график. Построим прямую по двум точкам (0;14) и (7;0), которые легко получить, если найти точки пересечения с осями координат
х1 |
0 |
7 |
(на рисунке прямая 1) |
|
х2 |
14 |
0 |
||
|
Граничная прямая делит плоскость на две полуплоскости. Возьмем в любой из полуплоскостей точку (в качестве нее проще всего взять начало координат – О (0;0)) и подставим ее координаты в неравенство 2х1+х2 14. Если координаты точки удовлетворяют этому неравенству, то вся полуплоскость, где лежит данная точка, является решением этого неравенства. Если нет, то решением неравенства является другая полуплоскость.
При подстановке значений х1=0 и х2=0 в первое неравенство получаем 0 14; следовательно, область решения этого неравенства включает начало координат (берется нижняя полуплоскость).
Аналогично строим область решения остальных неравенств х1+3х2=15
х1 |
|
0 |
|
15 |
(на рисунке прямая 2) |
|
|
||||
|
|
|
|||
х2 |
|
15 |
|
0 |
|
х1+3х2 15 при х1=0, х2=0, 0 15 неравенство выполняется, берется нижняя полуплоскость.
х1=6 (на рисунке прямая 3) неравенство выполняется, следовательно область решений включает начало координат.
х2=4 (на рисунке прямая 4) неравенство выполняется, берется нижняя полуплоскость.
Находим общую область полуплоскостей решений, учитывая при этом условия неотрицательности, означающие, что область расположена в I четверти, т.к. по условию задачи х1 0, х2 0.
23
Замечание. Если граничная прямая проходит через начало координат, то вместо точки О (0;0) необходимо испытать другую точку.
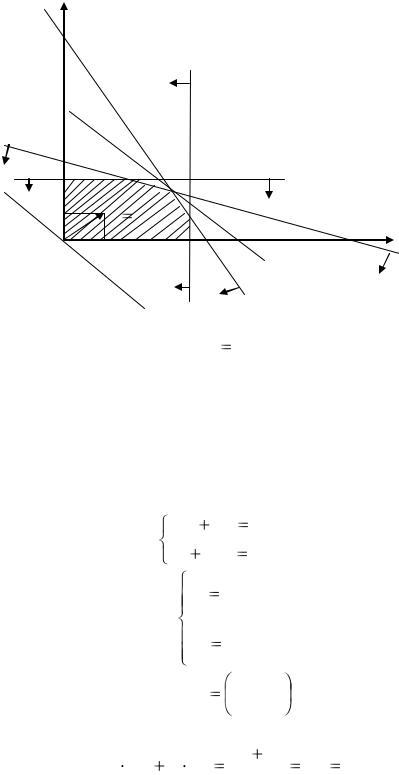
Полученную область допустимых решений, выпуклый многоугольник ОАВСDЕ отметим на рис. 13 штриховкой.
Х2
14
5 |
|
|
4 |
В |
(4) |
|
|
|
А |
|
С |
2 |
|
n |
(2;2) |
D |
|
|
||
|
|
|
|
Е |
|
|
||
О |
2 |
|
6 |
7 |
|
|
15 |
Х1 |
|
|
|
|
|||||
|
|
|
|
(1) |
|
|
||
|
|
|
|
(3) |
|
|
|
|
|
|
|
Рис. 13 |
|
|
|||
|
|
|
|
|
|
|||
Изобразим целевой |
вектор |
|
n (2;2) . |
Его координаты – это |
||||
коэффициенты целевой функции Z. Перпендикулярно вектору строим линию уровня Z=2х1+2х2=0 и передвиn гаем параллельно самой себе в направлении, которое указывает вектор.
Т.к. у нас задача максимизации, то последняя точка выхода из области и будет точкой максимума. В ней функция Z=2х1+2х2 принимает максимальное значение – это точка С. Точка С лежит на пересечении прямых (1) и (2). Для определения её координат решим систему уравнений:
2х1 |
х2 |
14, |
|
||||||||
х1 3х2 |
15. |
|
|||||||||
х |
|
27 |
, |
|
|
|
|
||||
|
|
|
|
|
|
||||||
1 |
5 |
|
|
|
|
|
|
|
|||
Получаем |
|
|
|
|
|
|
|
||||
|
|
16 |
|
|
|
|
|
|
|||
х2 |
|
. |
|
|
|
|
|||||
|
|
|
|
|
|||||||
|
5 |
|
|
|
|
|
|
|
|||
Оптимальный план задачи Х * |
|
27 |
; |
16 |
. Подставляя найденные |
||||||
|
|
|
|||||||||
|
5 |
|
|
5 |
|
||||||
значения в целевую функцию, получим:
Zmax= 2 |
27 |
2 |
16 |
54 |
32 |
86 |
17,2 . |
|||
5 |
|
5 |
|
|
5 |
|
5 |
|||
|
|
|
|
|
||||||
24
Пример 2. Решить задачу графическим методом.
Z=4x1+2x2→min,
4х1 х2 0,
2х1 х2 6, х1 2х2 12,
х1 х2 0,
х1 3,
х1 0; х2 0.
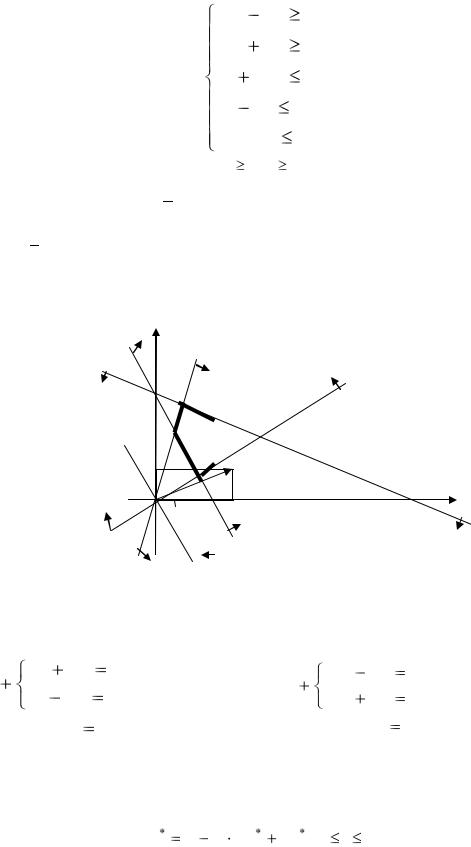
Решение. Строим область допустимых решений – многоугольник ABCDE. Целевой вектор n =(4;2). Перпендикулярно вектору строим линию уровня. Перемещаем линию уровня в направлении, противоположном вектору n , так как решается задача минимизации. Минимум достигается на отрезке АВ, т.к. линия уровня параллельна прямой, на которой лежит отрезок АВ. Задача имеет бесконечное множество оптимальных решений
(рис. 14).
|
(2) |
|
|
|
|
|
|
() |
|
|
|
|
(5) |
(4) |
|
|
|
|
|
||||
Х2 |
6 |
|
С |
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
D |
|
|
|
4 В |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е |
|
|
|
2 |
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
О |
1 |
2 |
|
3 4 |
12 |
Х1 |
|
|
|
|||||
|
|
|
|
|
|
|
(3) |
|
|
|
|
|
|
Рис. 14 |
|
|
|
|
|
|
|
|
Найдем координаты точек А и В, решая соответствующие системы
уравнений. |
|
т. А |
т. В |
|
2х |
х2 |
6 |
(2), |
|
4х1 |
х2 |
0 |
(1), |
|
|
х1 |
х2 |
0 |
(4), |
|
|
2х1 |
х2 |
6 |
(2), |
|
3х |
|
6, |
|
|
|
6х1 |
|
6, |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
х1=2, х2=2, |
|
|
|
х1=1, х2=4, |
|
||||
|
Х1*=(2; 2). |
|
|
|
Х2*=(1; 4). |
|
||||
Следовательно, любое оптимальное решение Х* равно: |
|
|
||||||||
|
|
|
|
Х (1 t) Х 1 |
tХ 2 , 0 t |
1. |
|
|
||
Вычисляем Z max=4·2+2·2=12. |
|
|
|
|
|
|||||
25
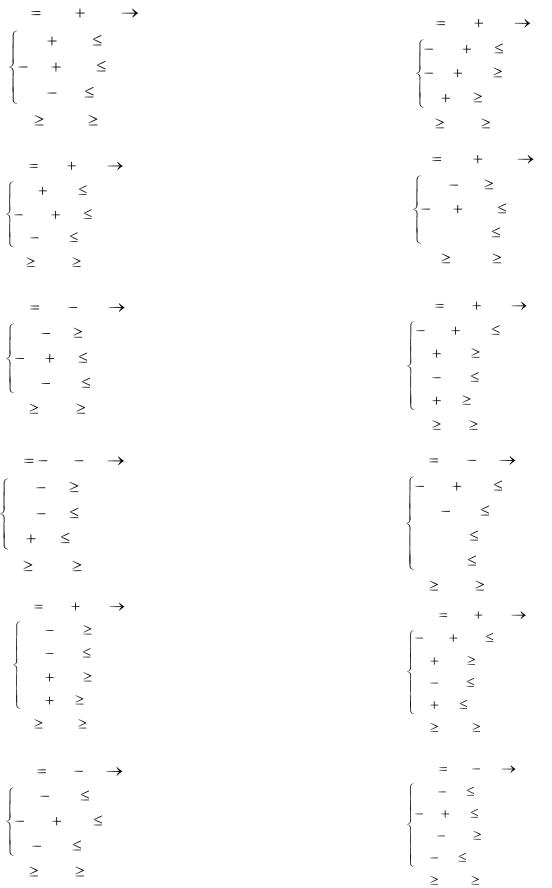
Решить графическим методом следующие задачи линейного программирования
1. Z |
|
4x1 |
2x2 |
max |
2.Z |
5x1 |
|
5x2 |
max |
|||||
2x1 |
|
|
3x2 |
18, |
|
|
||||||||
|
|
|
2x1 |
|
x2 |
2, |
||||||||
x1 |
|
3x2 |
9, |
|
|
|||||||||
|
|
x1 |
3x2 |
9, |
|
|||||||||
|
|
|
|
|
|
|
|
|
||||||
2x1 |
|
|
x2 |
10, |
|
x1 |
x2 |
|
3, |
|
|
|||
x1 |
|
0, x2 |
0. |
|
x |
0, x |
|
0. |
|
|||||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
3.Z |
|
2x1 |
4x2 |
|
max |
4. Z |
3x1 |
|
2x2 |
max |
||||
|
|
|
|
|
|
|
|
|
||||||
3x1 |
|
|
2x2 |
11, |
|
2x1 |
x2 |
0, |
|
|||||
2x1 |
|
x2 |
0, |
|
x1 |
2x2 |
3, |
|||||||
x |
3x |
0, |
|
|
|
|
x2 |
3, |
|
|||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
0, x |
0. |
|
|
x1 |
0, x2 |
0. |
|
||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
5.Z |
|
5x1 |
3x2 |
min |
6.Z |
4x1 |
|
2x2 |
min |
|||||
4x x |
0, |
|
|
3x1 |
2x2 |
6, |
|
|||||||
1 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
x1 |
|
|
x2 |
3, |
|
x1 |
2x2 |
|
10, |
|
||||
2x1 |
|
3x2 |
6, |
|
x1 |
3x2 |
|
6, |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
x1 |
|
0, x2 |
0. |
|
x1 |
x2 |
|
3, |
|
|
||||
|
|
x1 |
0, x |
|
0. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
7.Z |
|
3x1 |
x2 |
|
min |
8.Z |
3x1 |
|
x2 |
|
max |
|||
4x x |
0, |
|
|
3x1 |
2x2 |
6, |
|
|||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2x x |
0, |
|
|
2x1 |
3x2 6, |
|
||||||||
1 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
x |
x |
|
3, |
|
|
x1 |
|
|
|
6, |
|
|
||
1 |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
x1 |
0, x2 |
0. |
|
|
|
x2 |
|
6, |
|
|
||||
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
x1 |
0, x2 |
|
0. |
|
||
9.Z |
|
4x1 |
6x2 |
max |
10.Z |
2x1 |
|
4x2 |
max |
|||||
4x1 |
|
|
5x2 |
0, |
|
|
||||||||
|
|
|
3x1 |
2x2 |
6, |
|
||||||||
2x1 |
|
|
3x2 |
0, |
|
|
||||||||
|
|
|
x1 |
2x2 |
|
10, |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
||||
2x1 |
|
|
3x2 |
6, |
|
x1 |
5x2 |
|
5, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
||||
2x1 |
|
|
x2 |
2, |
|
|
x1 |
x2 |
|
4, |
|
|
||
x1 |
|
0, x2 |
0. |
|
|
x |
0, x |
|
0. |
|
|
|||
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
|
|
11.Z |
|
|
5x |
x |
|
max |
12.Z |
3x1 |
|
x2 |
|
min |
||
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
2x1 |
|
|
3x2 |
0, |
|
2x1 |
x2 |
|
4, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||||
5x1 |
|
9x2 |
45, |
|
x1 |
x2 |
|
2, |
|
|
||||
|
|
3x1 |
2x2 |
|
0, |
|
|
|||||||
x1 |
|
2x2 |
4, |
|
|
|
|
|
||||||
|
|
|
x1 |
x2 |
0, |
|
|
|||||||
x1 |
0, x2 |
0. |
|
|
|
|
||||||||
|
|
x1 |
0, x2 |
|
0. |
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
||||
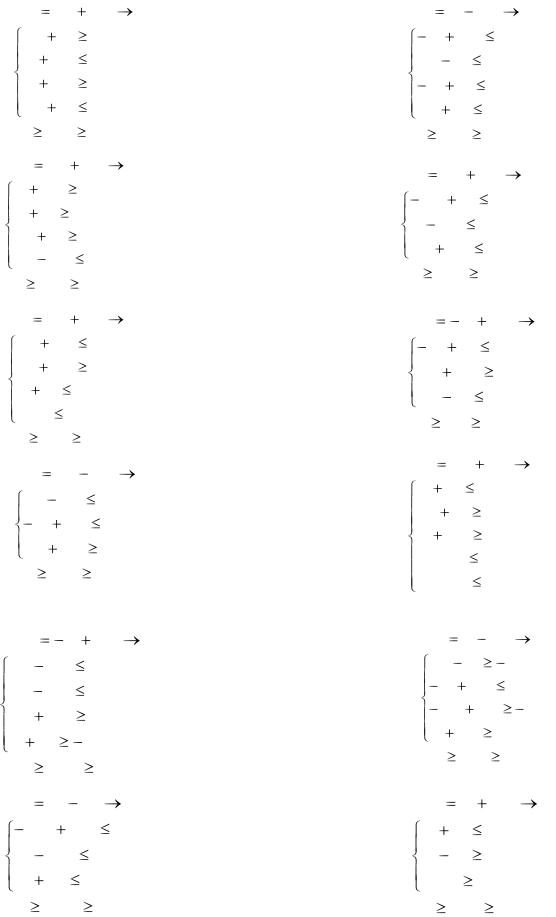
13.Z |
2x1 |
|
4x2 |
min |
|
2x1 |
x2 |
|
9, |
|
|
x1 |
2x2 |
|
15, |
|
|
x1 |
2x2 |
|
9, |
|
|
2x1 |
x2 |
|
15, |
|
|
x1 |
0, x2 |
|
0. |
|
|
15.Z |
2x1 |
3x2 |
max |
||
x1 |
2x2 |
2, |
|
||
x1 |
x2 |
2, |
|
|
|
2x1 |
x2 |
4, |
|
||
2x1 |
3x2 |
|
0, |
|
|
x1 |
0, x2 |
0. |
|
||
17.Z |
7x1 |
6x2 |
max |
||
2x1 |
5x2 |
|
10, |
|
|
5x1 |
2x2 |
|
10, |
|
|
x1 |
x2 |
6, |
|
|
|
|
x2 |
5, |
|
|
|
x1 |
0, x2 |
0. |
|
||
19.Z |
2x1 |
|
4x2 |
max |
|
8x1 |
5x2 |
16, |
|
||
|
x1 |
3x2 |
2, |
|
|
2x1 |
7x2 |
9, |
|
||
x1 |
0, x2 |
|
0. |
|
|
21. Z |
|
x1 |
|
4x2 |
min |
2x1 3x2 6,
3x1 2x2 6,
2x1 3x2 0,
x1 |
x2 |
1, |
x1 |
0, x2 |
0. |
23. Z x1 x2 max
2x1 3x2 9, x1 2x2 2,
x1 x2 8, x1 0, x2 0.
26
14.Z x1 3x2 min
x1 |
|
2x2 |
12, |
|
||
2x1 |
|
x2 |
6, |
|
||
x1 |
|
x2 |
3, |
|
||
2x1 |
|
x2 |
6, |
|
||
x1 |
0, x2 |
0. |
|
|||
16.Z |
2x1 |
3x2 |
max |
|||
4x1 |
|
x2 |
|
4, |
|
|
x1 |
2x2 |
4, |
|
|
||
2x1 |
|
3x2 |
12, |
|
||
x1 |
0, x2 |
0. |
|
|||
18.Z |
|
|
x1 |
2x2 |
max |
|
x1 |
|
x2 |
|
2, |
|
|
5x1 |
|
2x2 |
10, |
|
||
3x1 |
|
x2 |
3, |
|
||
x1 |
|
0, x |
0. |
|
||
20.Z |
|
3x1 |
3x2 |
max |
||
x1 |
|
x2 |
4, |
|
|
|
3x1 |
|
x2 |
4, |
|
||
x1 |
|
5x2 |
4, |
|
||
x1 |
|
|
|
3, |
|
|
|
|
x2 |
3. |
|
||
22.Z |
|
x1 |
2x2 |
min |
||
2x1 |
x2 |
2, |
|
|||
|
x1 |
2x2 |
7, |
|
||
|
4x1 |
3x2 |
12, |
|||
x1 |
|
3x2 |
18, |
|
||
x1 |
|
0, x2 |
0. |
|
||
24.Z |
|
x1 |
2x2 |
min |
||
x1 |
|
x2 |
8, |
|
||
x1 |
|
x2 |
2, |
|
||
x1 |
|
|
|
3, |
|
|
x1 |
|
0, x2 |
0. |
|
||
27
25.Z |
x1 |
x2 min |
x1 |
x2 |
1, |
3x1 |
2x2 |
6, |
3x1 x2 |
9, |
|
x1 |
0, x2 |
0. |
4. Задача определения оптимального плана выпуска продукции
4.1. Краткие теоретические сведения
Рассмотрим задачу планирования работы некоторого предприятия, выпускающего n видов продукции. На производство этой продукции требуются различные виды ресурсов (m), затраты которых ограничены на предприятии. В зависимости от объема произведенной каждой из n видов продукции будут затрачиваться различные объемы ресурсов и различная суммарная выручка от реализации выпущенной продукции.
Для составления модели задачи выпуска продукции обозначим через aij – расход i-го вида ресурса на производство единицы j-го вида продукции i 1, m , j 1, n ; bi – затраты i-го вида ресурса; Сj – цена единицы j-го вида продукции; xj – количество продукции j-го вида продукции, выпущенной предприятием; Х 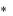 (x 1 , x 2 ,..., x n ) – искомый план
(x 1 , x 2 ,..., x n ) – искомый план
выпуска продукции.
Ограничения по запасам ресурсов записываются в следующем виде:
a11 x1 |
a12 x2 |
... |
a1n xn |
b1 , |
|
a21 x1 |
a22 x2 |
... |
a2n xn |
b2 , |
(4.1) |
............................................ |
|
|
|||
am1 x1 |
am2 x2 |
... |
amn xn |
bm . |
|
и означают, что расход i-го вида ресурса на выпуск всех видов продукции не может превышать имеющихся запасов ресурсов.
По условию задачи, выпуск продукции – величина неотрицательная
|
|
|
|
|
|
|
|
(4.2) |
x j |
0 ( j |
1, n). |
|
|
|
|||
Необходимо определить |
план |
выпуска |
продукции X , |
при котором |
||||
выручка от реализации всей продукции была максимальной |
|
|||||||
Z c1 x1 |
c2 x2 |
... cn xn |
max . |
(4.3) |
||||
Полученную модель можно записать более компактно:
n |
|
|
|
|
|
|
|
|
|
aij |
x j |
bi , |
i |
1, m , |
(4.4) |
||||
j 1 |
|
|
|
|
|
|
|
(4.5) |
|
|
|
|
|
|
|
|
|
||
|
x j |
0, ( j |
|
1, n), |
|||||
|
|
|
|||||||
n |
|
|
|
|
|
|
|
(4.6) |
|
Z |
cij |
x j |
max . |
||||||
|
|||||||||
j |
1 |
|
|
|
|
|
|
|
|
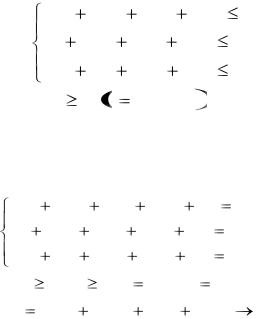
28
4.2. Составление модели задачи
Пусть для выпуска четырех видов продукции Р1, Р2, Р3, Р4 на предприятии используют три вида ресурсов S1, S2, S3. Запасы ресурсов, нормы расхода ресурсов и цены реализации единицы продукции приведены в таблице.
Вид |
Запасы |
Норма расхода ресурсов на ед. продукции |
||||
ресурса |
ресурсов |
Р1 |
Р2 |
Р3 |
Р4 |
|
S1 |
250 |
4 |
2 |
3 |
2 |
|
S2 |
400 |
1 |
4 |
5 |
7 |
|
S3 |
450 |
2 |
1 |
4 |
6 |
|
Цена реализации |
15 |
10 |
8 |
12 |
||
ед. продукции(сj) |
||||||
|
|
|
|
|||
Требуется определить план выпуска продукции, обеспечивающий наибольшую прибыль.
Составим математическую модель исходной задачи. В качестве неизвестных примем объем выпуска продукции j-го вида xj. Пусть
требуется максимизировать функцию |
|
|
|
|||
Z=15x1+10x2+8x3+12x4→max |
(4.7) |
|||||
при условиях |
|
|
|
|
|
|
4x1 |
2x2 |
3x3 |
2x4 |
250, |
|
|
x1 |
4x2 |
5x3 |
7x4 |
400, |
(4.8) |
|
2x1 |
x2 |
4x3 |
6x4 |
450. |
||
|
||||||
x j |
0, j |
1, 2, 3, 4 . |
|
|
||
Приведем математическую модель исходной задачи к каноническому виду, добавим в левые части ограничений неотрицательные балансовые переменные:
4x1 |
2x2 |
3x3 |
|
2x4 |
S1 |
250, |
||||
x1 |
4x |
2 |
5x3 |
7x4 |
S 2 |
400, |
||||
2x1 |
x |
2 |
4x3 |
6x4 |
S3 |
450, |
||||
|
|
|
|
|
|
|
|
|||
x j |
0, Si |
0 ( j |
1, 4), (i 1, 3). |
|||||||
Z |
15x1 |
10x2 |
8x3 |
12x4 |
|
max |
||||
Значение балансовых переменных Si показывают объемы неизрасходованных ресурсов.
4.3. Анализ решения задачи с помощью ППП QM for Windows
Для решения данной задачи используется пакет QM for Windows. Двойным щелчком по пиктограмме загрузим программу. На экране откроется основное окно. Выберем в строке меню Module раздел Linear Programming. Далее выберем пункт меню File, в нем подпункт New
(рис. 15).
29
Рис. 15.
Появится следующая таблица, предназначенная для ввода данных (рис.
16).
Рис. 16.
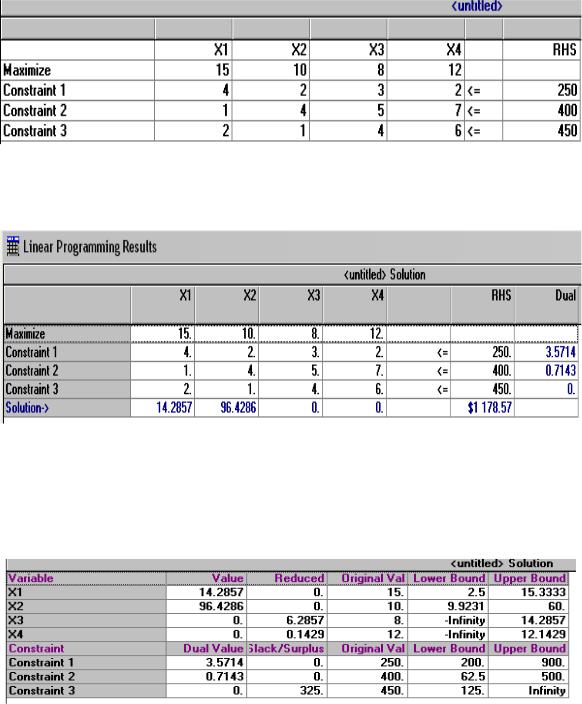
Задаем в строке Number of constrains количество ограничений (для нашего параметра – 3), в строке Number of variables – количество переменных (для нашего параметра – 4) и тип целевой функции, ставим точку на максимум. Нажимаем кнопку «ОК».
Появится диалоговое окно, в которое необходимо ввести исходные данные задачи (рис.17).
Рис.17.
Встроку Maximize необходимо ввести коэффициенты целевой функции
Z (цена реализации ед. продукции Сj). В строки Constraint 1, 2, 3 вводятся коэффициенты ограничений задачи при Хj (нормы расхода ресурсов aij). Тип ограничения задан (<=), при необходимости знак ограничения можно менять щелчком по стрелке вниз, поставив курсор в соответствующую позицию. В столбец RHS вводятся значения правых частей ограничений (запасы ресурсов bi).
Врезультате ввода данные на экране будут выглядеть следующим образом (рис. 18).
30
Рис. 18.
Если данные введены верно, нажмите клавишу Solve, и получим решение задачи. Введенные данные можно исправить нажатием клавиши
Edit data.
Рис. 19.
На рис.19 приведено окно Results. В строке Solution данного отчета под соответствующими переменными Хj указаны их значения в оптимальном плане, т.е. объемы j-й продукции, выпущенной предприятием, а также в столбце RHS – значение целевой функции Z. В столбце Dual отражены двойственные оценки оптимального плана.
Рис.20.
На рис. 20 приведено окно Ranging (размах). В верхней части этого отчета указаны границы устойчивости переменных исходной задачи. В столбце Value (величина) записаны значения переменных Хj исходной задачи. Столбец Reduced cost (lj) – есть превышение затрат на выпуск единицы j-го вида продукции над ценой. В столбце Original Value указаны исходные цены реализации за единицу соответствующего вида продукции. В последних двух столбцах представлены границы изменения цен. Lower Bound – нижний предел устойчивости для цен, Upper bound – верхний предел устойчивости для цен.
