I. Основы интегрирования

§ 1. Табличное интегрирование

Функция называется первообразной для функции , если или . Например, – первообразная для , поскольку .

Неопределённый интеграл для функции – это множество всех её первообразных: . Константа C подчёркивает, что первообразных для одной и той же функции бесконечно много, но они отличаются только на постоянное число. Например,

,

поэтому общий вид первообразных для функции – это . Значит, .

Аналогично , поскольку не только , но и

, и т.д.

Простейшая таблица неопределённых интегралов

1) ,	7) ,
2) ,	8) ,
3) ,	9) ,
4) ,	10) ,
5) ,	11) ,
6) ,	где в интегралах 8 – 10 .

Эти интегралы называют табличными. Ни один из них не приводится к другому, но любой интеграл, не учтённый в таблице, либо сводится разными методами к указанным, либо вовсе не выражается в элементарных функциях.

Трудность интегрирования по сравнению с дифференцированием связана со значительно меньшим набором свойств и правил. Так, справедливы арифметические свойства интегралов

;

для любого действительного числа ,

однако нет (и не может быть) никаких общих формул для интеграла от произведения, частного, а также от сложной функции.

Более того, небольшое изменение функции под знаком интеграла (подынтегральной функции) может заметно изменить ответ или даже метод решения. Сравните интегралы

а) , б) ,

в) ,

г) .

В то же время производные от подынтегральных функций находятся одним и тем же способом и внешне почти совпадают.

Именно поэтому приходится изучать разные методы интегрирования.

Основное правило табличного интегрирования:

Пусть – любые числа и при этом . Если , то

.

Пример 1. Известно (1-й табличный интеграл), что . Тогда

.

Коэффициент a может быть дробным и (или) отрицательным:

.

Вместо 1/1 можно не указывать ничего, вместо –9/1 записывать –9.

Пример 2. По основному правилу табличного интегрирования

, поскольку ;

, потому что ;

, так как ;

(здесь );

;

.

Однако таким способом не найти: аргумент нелинеен относительно х (этот интеграл не выражается в элементарных функциях).

Часто встречается ошибка: интеграл находят как . Правильное решение – свести к интегралу 9 из таблицы:

.

Продифференцировав и упростив, получим именно , в то время как

,

и отличие как раз связано с .

Другая ошибка – наоборот, найти как , применив равенство . На самом деле . Правильное решение: .

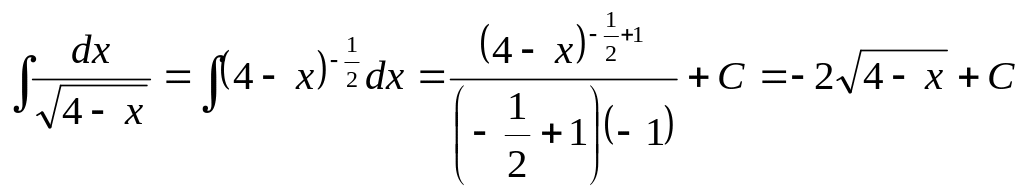ТИ1. А) Найдите производную; Б) найдите дифференциал функции;

В) восстановите функцию; Г) найдите интеграл:

	А	Б	В	Г
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

Пример 3. Задание ТИ1 удобно решать так:

1) и, как следствие, . Тогда и соответственно . Также ;

2) , потому . Наоборот, , и тогда . Кроме того, ;

3) , . Тогда , и потому . Значит, .

ТИ2. Найдите неопределённые интегралы от дробных функций, разложив дробь на две дроби, упростив и сведя всё к интегралам от степенных функций:

1)

2)

3) .

Пример 4. С учётом арифметических свойств неопределённого интеграла,

а) ;

б) .

ТИ3. Таким же образом, как в задании ТИ2, найдите неопределённые интегралы от дробно-иррациональных функций

1) ;

2) ;

3) .

Пример 5. Разложим дробь на сумму или разность функций, тогда

а)

;

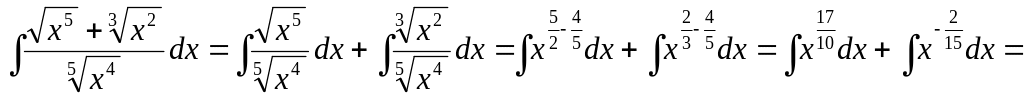
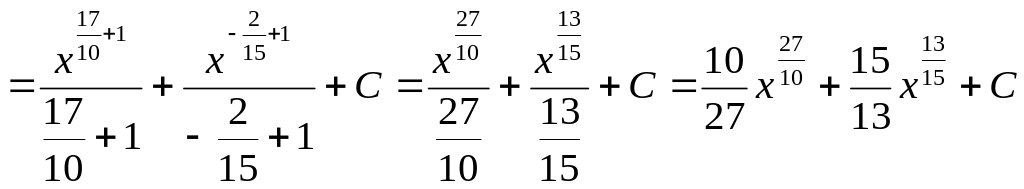б)

.

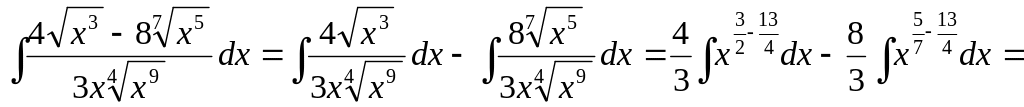
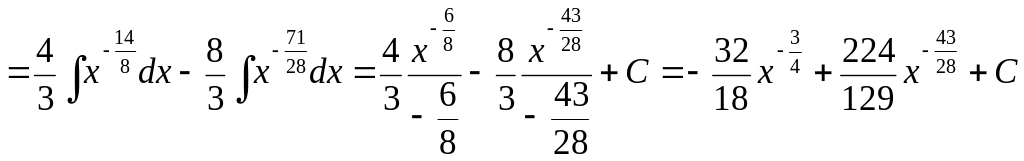Здесь . Также .

ТИ4. Проинтегрируйте сумму или разность функций при помощи двух табличных интегралов:

1) ;

2) ;

3) ;

4) ;

5) .

Указание к п. 4 и 5: учтите, что и , и сведите всё к одной функции – к или .

Пример 6. Легко убедиться, что

а) ;

б)

.

При интегрировании дробно-рациональных функций следует помнить, что

; ; ,

и т.п., что нетрудно проверить, взяв производную. На самом деле

; ; ,

что тоже проверяется дифференцированием. Также см. Замечание на стр. 6.

ТИ5. Найдите интегралы от функций

1) ;

2) ;

3) ;

4) .

Пример 7. Согласно таблице интегралов,

а) ; б) .

ТИ6. Проинтегрируйте, избавившись от коэффициента перед квадратом:

1) ;

2) ;

3) ;

4) .

Пример 8. Вынесем коэффициент за скобку, а затем за знак интеграла:

а) ;

б) .

ТИ7. Найдите интегралы

1) ;

2) .

Пример 9. По таблице находим, что

а) , где ;

б) (знак перед числом 3 ни на что не влияет).

ТИ8. Избавившись от коэффициента перед квадратом, найдите интегралы

1) ;

2) ;

3) ;

4) .

Пример 10 (здесь ).

а) ;

б) .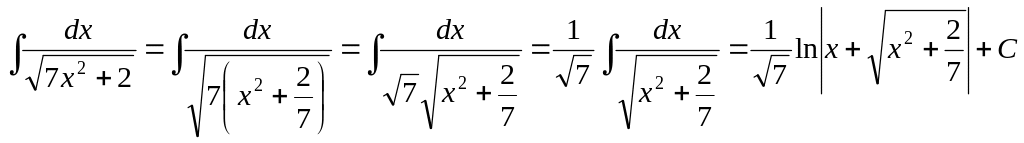

ТИ9. На основе интеграла (при ) найдите

1) ;

2)

3) ;

4) .

Пример 11. Задание ТИ9 решается так:

а) ;

б) ;

в)

;

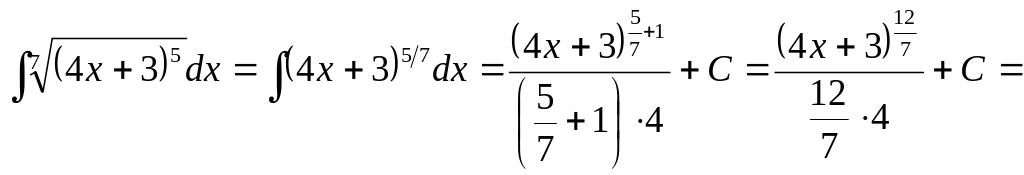
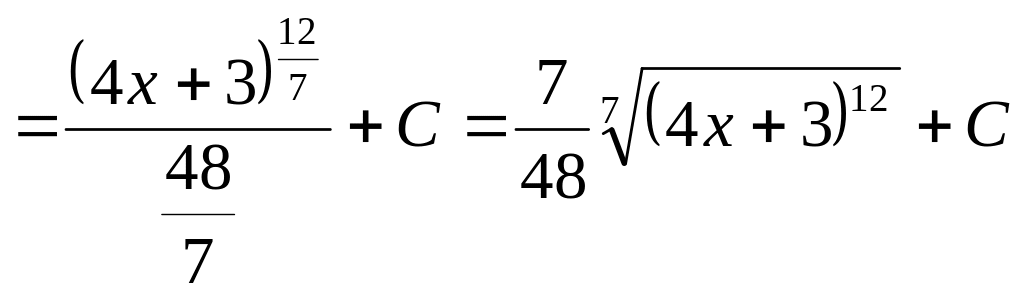г)

.

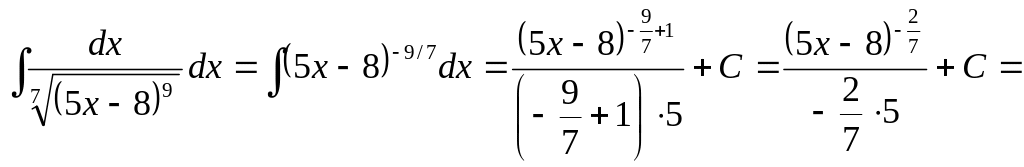
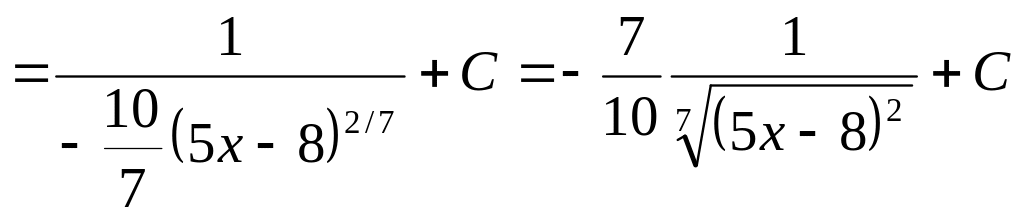ТИ10. Зная, что , найдите

1) ;

2) .

Пример 12. По основному правилу табличного интегрирования

а) – логарифм знаменателя делим на коэффициент перед переменной;

б) .

ТИ11. Учитывая, что , найдите

1) ;

2) .

Пример 13. Проверьте дифференцированием, что

а) (здесь );

б) .

ТИ12. На основе интеграла найдите

.

Пример 14. .

ТИ 13. С учётом формулы найдите

.

Пример 15. .

ТИ14. Зная, что , найдите

.

Пример 16. .

ТИ15. Учитывая формулу , найдите

.

Пример 17. .

ТИ16. На основе табличного интеграла найдите

.

Пример 18. При помощи производной можно проверить, что

а) ;

б) .

ТИ17. На основе табличного интеграла найдите

.

Пример 19. Легко видеть, что

а)

б) .

ТИ18. Зная, что , найдите

.

Пример 20. .