
617_Zabelin_L.JU._Osnovy_komp'juternoj_grafiki_
.pdf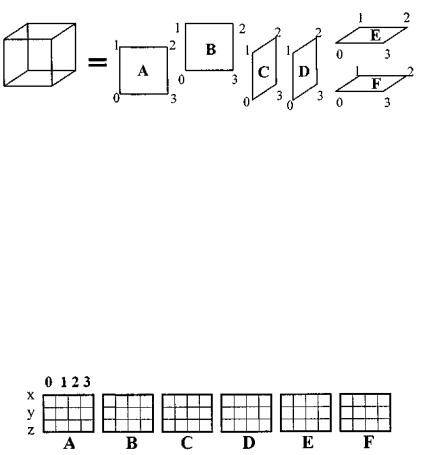
Пример. Чтобы понять структуры данных, которые используются в векторной полигональной модели, возьмем куб и рассмотрим, как можно организовать описание такого объекта в структурах данных.
Можно использовать несколько способов. Первый способ показан на ри-
сунках 8.6. и 8.7.
ГраньA (xA0 , yA0 , zA0 ), (xA1, yA1, zA1), (xA2 , yA2 , zA2 ), (xA3 , yA3 , zA3 ) ГраньB (xB0 , yB0 , zB0 ), (xB1, yB1, zB1), (xB 2 , yB 2 , zB 2 ), (xB3 , yB3 , zB3 ) ГраньC (xC 0 , yC 0 , zC 0 ), (xC1, yC1, zC1), (xC 2 , yC 2 , zC 2 ), (xC 3 , yC 3 , zC 3 ) ГраньD (xD0 , yD0 , zD0 ), (xD1, yD1, zD1), (xD 2 , yD 2 , zD 2 ), (xD3 , yD3 , zD3 ) ГраньE (xE 0 , yE 0 , zE 0 ), (xE1, yE1, zE1), (xE 2 , yE 2 , zE 2 ), (xE 3 , yE 3 , zE 3 ) ГраньF (xF 0 , yF 0 , zF 0 ), (xF1, yF1, zF1), (xF 2 , yF 2 , zF 2 ), (xF 3 , yF 3 , zF 3 )
Рисунок 8.6. – Первый способ. Сохраняем все грани в отдельности
Рисунок 8.7. –Схематичное изображение первого способа
В компьютерной программе такой способ описания объекта можно реализовать весьма разнообразно, но принципиально это мало что изменяет – так или иначе в памяти необходимо сохранять координаты вершин граней плюс некоторую информацию в качестве накладных затрат. Объем памяти, необходимый для описания куба можно рассчитать следующим образом:
П1 6 4 3 Рв |
(8.8.) |
где Рв – разрядность чисел, необходимая для представления координат.
Шесть граней здесь описываются 24 вершинами. Такое представление избыточно – каждая вершина записана трижды. Не учитывается то, что у граней есть общие вершины.
51
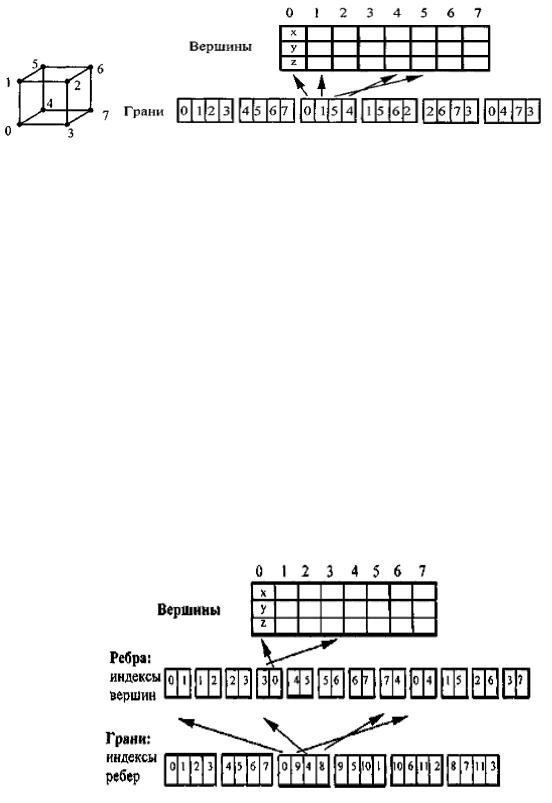
Для второго способа, варианта координаты восьми вершин сохраняются без повторов. Вершины пронумерованы, а каждая грань дается в виде списка индексов вершин (указателей на вершины).
Рисунок 8.8. – Второй способ
В этом случае затраты памяти составят:
П2 8 3 Рв 6 4 Pиндекс |
(8.9.) |
где Рв – разрядность координат вершин, Риндекс – разрядность индексов.
Третий способ основывается на иерархии: вершины-ребра-грани (в литературе его иногда называют линейно-узловой моделью).
Затраты памяти:
П3 8 3 Рв 12 2 Pинд.вершин 6 4 Ринд. ребер (8.10.)
где Рв – разрядность координат, Ринд вершин и Ринд.ребер – разрядность индексов вершин и ребер соответственно.
Рисунок 8.9. – Третий способ
52
Сравним три способа описания полигональной модели по следующим параметрам:
А) Объем памяти. Для сравнения объемов памяти этих трех вариантов необходимо определиться с разрядностью данных. Когда разрядность для координат больше, чем для индексов, то ощутимо преимущество второго и третьего вариантов. Наиболее экономичным можно считать второй вариант. Необходимо заметить, что такой вывод мы сделали для куба. Для других типов объектов соотношение вариантов может быть иным.
Б) Скорость вывода полигонов. Если для полигонов необходимо рисовать линию контура и точки заполнения, то первый и второй варианты близки по быстродействию – и контуры, и заполнения рисуются одинаково. Отличия в том, что для второго варианта сначала надо выбирать индекс вершины, что замедляет процесс вывода. В обоих случаях для смежных граней повторно рисуется общая часть контура. Для третьего варианта можно предусмотреть более совершенный способ рисования контура – каждая линия будет рисоваться только один раз, если в массивах описания ребер предусмотреть бит, означающий, что это ребро уже нарисовано. Это обуславливает преимущества третьего варианта по быстродействию. Блокирование повторного рисования линий контуров смежных граней позволяет решить также проблему искажения стиля линий, если линии контуров не сплошные, а, например, пунктирные.
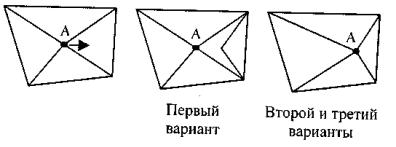
В) Топологический аспект. Представим, что имеется несколько смежных граней. Что будет, если изменить координаты одной вершины в структурах данных? Результат приведен на рисунке 8.10.
Рисунок 8.10. – Топологический аспект
Поскольку для второго и третьего вариантов каждая вершина сохраняется в одном экземпляре, то изменение ее координат автоматически приводит к изменению всех граней, в описании которых сохраняется индекс этой вершины. Это полезно, например, в геоинформационных системах при описании соседних земельных участков или других смежных объектов. Следует заметить, что подобного результата можно достичь и при структуре данных, соответствующей первому варианту. Можно предусмотреть поиск других вершин, координаты которых совпадают с координатами точки А. Иначе говоря, поддержка такой операции может быть обеспечена как структурами данных, так и алгоритмически. Однако когда нужно разъединить смежные грани, то для второго и третье-
53
го вариантов это сложнее, чем для первого – необходимо записать в массивы новую вершину, новые ребра и определить индексы в массивах граней.
Положительные черты векторной полигональной модели:
·удобство масштабирования объектов. При увеличении или уменьшении объекты выглядят более качественно, чем при растровых моделях описания. Диапазон масштабирования определяется точностью аппроксимации и разрядностью чисел для представления координат вершин;
·небольшой объем данных для описания простых поверхностей, которые адекватно аппроксимируются плоскими гранями;
·необходимость вычислять только координаты вершин при преобразованиях систем координат или перемещении объектов;
·аппаратная поддержка многих операций в современных графических видеосистемах, которая обуславливает достаточную скорость для анимации.
Недостатки полигональной модели:
·сложные алгоритмы визуализации для создания реалистичных изображений; сложные алгоритмы выполнения топологических операций, таких,
например, как разрезы; аппроксимация плоскими гранями приводит к погрешности моделирования.
При моделировании поверхностей, которые имеют сложную фрактальную форму, обычно невозможно увеличивать количество граней из-за ограничений по быстродействию и объему памяти компьютера.
Рассмотрим воксельное представление.
Смысл воксельного представления – дискретизация пространства на равномерной сетке.
Воксельная модель – это трехмерный растр. Подобно тому, как пиксели располагаются на плоскости 2В-изображения, так и вокселы образовывают трехмерные объекты в определенном объеме. Воксел – это элемент объема
(voxel – volume element).
Каждый пиксель должен иметь свой цвет. Каждый воксел также имеет свой цвет, а, кроме того, прозрачность. Полная прозрачность воксела означает пустоту соответствующей точки объема. При моделировании объема каждый воксел представляет элемент объема определенного размера. Чем больше вокселов в определенном объеме и меньше размер вокселов, тем точнее моделируются трехмерные объекты – увеличивается разрешающая способность.
Для современной компьютерной графики воксельный метод считается одним из перспективных. Его используют в компьютерных системах для медицины (например, при сканировании томографом) Вокселы используются для графических устройств отображения, которые создают действительно объемные изображения [9].
54
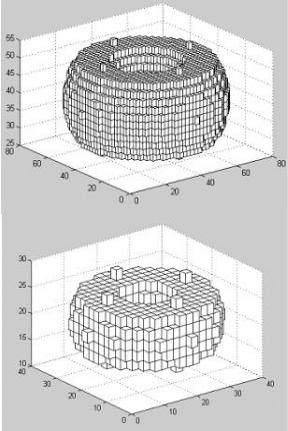
Рисунок 8.11. – Воксельная модель
Положительные черты воксельной модели:
позволяет достаточно просто описывать сложные объекты и сцены; простая процедура отображения объемных сцен;
простое выполнение топологических операций над отдельными объектами и сценой в целом. Например, просто выполняется показ разреза – для этого соответствующие вокселы можно сделать прозрачными.
Недостатки воксельной модели:
большое количество информации, необходимой для представления объемных данных. Например, объем 256x256x256 имеет небольшую разрешающую способность, но требует свыше 16 миллионов вокселов;
значительные затраты памяти ограничивают разрешающую способность, точность моделирования; большое количество вокселов обусловливает малую скорость создания изображений объемных сцен;
как и для любого растра, возникают проблемы при увеличении или
уменьшении изображения. Например, при увеличении ухудшается разрешающая способность изображения.
Существуют способы, которые оптимизируют воксельное представление. Например, октарные деревья, которые позволяют хранить только части пространства, занятые объектом.
Рассмотрим конструктивную геометрию (Представление CSG моделей).
Объект задается набором примитивов и операций над ними.
55

Примитивы – «строительные блоки» объекта. Чаще всего это куб, сфера, цилиндр и т.п. Операции – теоретико-множественные операции (объединение, пересечение, разность) и т.п. Геометрические преобразования – смещение, поворот, изменение размеров и т.п.
Если у нас в трёхмерном пространстве есть тело, то мы это пространство можем разбить на кубики (boxels). Для каждого кубика (i, j, k) мы можем указать, пересекается ли он с телом: то есть лежит ли он внутри, на границе или вне тела. Например, при моделировании головного мозга мы можем представить маленькими кубиками наполнение нашей черепной коробки, соответственно можно представить уплотнения и пустоты, чего нельзя сделать в других моделях.
Стаким подразбиением можно проводить набор операций:
·пересечение;
·объединение;
·вычитание.
Соответственно в результате можем получить более сложное тело.
Рисунок 8.12 – Примеры образования тел
Рассмотрим равномерную сетку. Эта модель описывает координаты отдельных точек поверхности следующим способом: каждому узлу сетки с индексами (i, j) приписывается значение высоты zij. Индексам (i, j) отвечают определенные значения координат (х, у). Расстояние между узлами одинаковое – dx по оси х и dy по оси y.
56
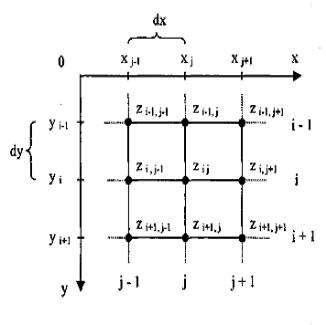
Рисунок 8.13. – Равномерная сетка
Фактически, такая модель – двумерный массив, растр, матрица, каждый элемент которой сохраняет значение высоты.
Не каждая поверхность может быть представлена этой моделью. Если в каждом узле записывается только одно значение высоты, то это означает, что поверхность описывается однозначной функцией z = f (х, у). Иначе говоря, это такая поверхность, которую любая вертикаль пересекает только один раз. Не могут моделироваться также вертикальные грани. Необходимо заметить, что для сетки не обязательно использовать только декартовые координаты. Например, для того чтобы описать поверхность шара однозначной функцией, можно использовать полярные координаты. Равномерная сетка часто используется для описания рельефа земной поверхности.
Положительные черты равномерной сетки:
простота описания поверхностей;
возможность быстро узнать высоту любой точки поверхности простой интерполяцией.
Недостатки равномерной сетки:
поверхности, которые соответствуют неоднозначной функции высоты в узлах сетки, не могут моделироваться;
для описания сложных поверхностей необходимо большое количество узлов, которое может быть ограничено объемом памяти компьютера;
описание отдельных типов поверхностей может быть сложнее, чем в других моделях. Например, многогранная поверхность требует избыточный объем данных для описания по сравнению с полигональной моделью.
Рассмотрим неравномерную сетку, изолинии. Неравномерной сеткой назовем модель описания поверхности в виде множества отдельных точек(x0 , y0 , z0 ),(x1 , y1 , z1 ),...,(xn 1 , yn 1, zn 1 ) , принадлежащих поверхности. Эти точки мо-
57
гут быть получены, например, в результате измерений поверхности какогонибудь объекта с помощью определенного оборудования.
Эту модель можно считать обобщением для некоторых рассмотренных нами моделей. Например, векторная полигональная модель и равномерная сетка могут считаться разновидностями неравномерной сетки.
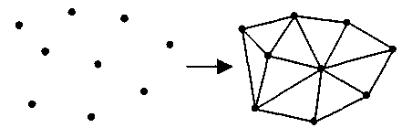
Рассмотрим модель поверхности в виде множества точечных значений, логически никак не связанных между собой. Неравномерность задания опорных точек усложняет определение координат для других точек поверхности, которые не совпадают с опорными точками. Нужны специальные методы пространственной интерполяции. Так, например, можно поставить такую задачу – по известным координатам (х, у) вычислить значения координаты z. Для этого необходимо найти несколько самых близких точек, а потом вычислить искомое значение z, исходя из взаимного расположения этих точек в проекции (х, у). Для равномерной сетки это намного проще – поиска фактически нет, мы сразу рассчитываем индексы самых близких опорных точек. Еще одна задача – отобразить поверхность. Эту задачу можно решать несколькими способами, в том числе триангуляцией. Процесс триангуляции можно представить себе так: сначала находим первые три самые близкие друг другу точки и получаем одну плоскую треугольную грань. Потом находим точку, ближайшую к этой грани, и образовываем смежную грань. И так далее, пока не останется ни одной отдельной точки.
Рисунок 8.14. – Метод триангуляции
Это общая схема, в литературе описано много разных способов триангуляции.
Рассмотрим еще один из вариантов описания поверхности – изолинии высоты. Любая изолиния состоит из точек, представляющих одно числовое значение какого-то показателя, в данном случае – значение высоты. Изолинии высоты также можно вообразить себе как контуры разреза поверхности горизонтальными плоскостями (поэтому для изолиний высоты часто применяется название "горизонтали").
58
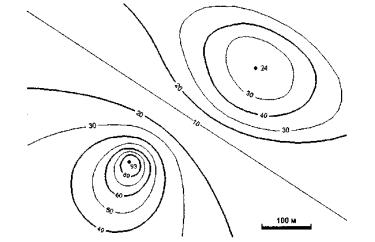
Рисунок 8.15. – Изолинии высоты
Описание поверхности изолиниями высоты часто используется, например, в картографии. По бумажной карте можно с определенной точностью рассчитать высоты в точках местности, углы наклона и прочие параметры рельефа.
Положительные черты неравномерной сетки: использование отдельных опорных точек, наиболее важных для заданной формы поверхности, обуславливает меньший объем информации по сравнению с другими моделями, например, с равномерной сеткой; наглядность показа рельефа поверхности изолиниями на картах, планах.
Недостатки: невозможность или сложность выполнения многих операций над поверхностями; сложные алгоритмы преобразования в другие формы описания поверхностей.
9.Координатные преобразования объектов
9.1.Общие вопросы преобразования
Вкомпьютерной графике часто применяются различные геометрические преобразования над объектами: вращение, сжатие, параллельный перенос и др.
Спомощью них, однократно описав топологию объекта, мы можем получить много различных его экземпляров. Обычно принято разделять преобразования первого рода (собственные движения, сохраняющие ориентацию углов) и преобразования второго рода (зеркальные движения, меняющие ее). К первым относят параллельный перенос, поворот и др., ко вторым – симметрии (относительно точки, прямой, окружности). Математически эти преобразования описываются матрицами преобразований [21].
Вкачестве модели здесь выступает описание поверхности трехмерного объекта, в виде некоторого подмножества точек декартова пространства. Поэтому рассматриваемые преобразования тесно связанны с системой координат. Координатный метод был введен в XVII веке французскими математиками Де-
59
картом и Ферма. В современной компьютерной графике широко используется координатный метод. Этому есть несколько причин:
Каждая точка на экране (или на бумаге при печати на принтере) задается координатами (например, пиксельными).
Координаты используются для описания объектов, которые будут отображаться как пространственные. Например, объекты микромира, объекты на поверхности Земли, объекты космического пространства и тому подобное.
При выполнении многих промежуточных действий отображения используют разные системы координат и преобразования из одной системы в другую.
9.2. Преобразование координат и преобразование объектов
Сначала рассмотрим общие вопросы преобразования координат. Пусть задана n-мерная система координат в базисе (k1, k2, ..., kn), описывающая положение точки в пространстве с помощью числовых значений ki. В компьютерной графике чаще всего используется двумерная (n=2) и трехмерная (n=3) системы координат [21]. Если задать другую, N-мерную, систему координат в базисе (m1, т2, .... mN) и поставить задачу определения координат в новой системе, зная координаты в старой, то решение (если оно существует), можно записать в таком виде:
m1 f1 (k1 , k2 ,..., kn ), |
|
|
|||||||
|
|
f2 (k1 , k2 |
,..., kn ), |
|
|||||
m2 |
(9.2.1.) |
||||||||
|
|
|
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
|
|
|
m |
N |
f |
N |
(k , k |
2 |
,..., k |
n |
) |
|
|
|
1 |
|
|
|
||||
где fi – функция пересчета i-й координаты.
Можно поставить и обратную задачу – по известным координатам (m1, т2, .... mN) определить координаты (k1, k2, ..., kn) . Решение обратной задачи запишем так:
k1 F1 (m1 , m2 ,..., mN ), |
|
|||||
|
|
F2 (m1 , m2 ,..., mN ), |
|
|||
k2 |
(9.2.2.) |
|||||
|
|
|
|
|
|
|
... |
|
|
|
|
|
|
k |
n |
F (m , m |
,..., m |
N |
) |
|
|
N 1 2 |
|
|
|
||
где Fi – функции обратного преобразования.
В случае, когда размерности систем координат не совпадают (п N), осуществить однозначное преобразование координат зачастую не удается. Например, по двумерным экранным координатам нельзя без дополнительных условий однозначно определить трехмерные координаты отображаемых объектов.
Преобразование объектов можно описать так. Пусть любая точка, которая принадлежит определенному объекту, имеет координаты (k1, k2, ..., kn) в
60
