Ишченко Информатсионно-аналитические модели проектов сетевое планирование 2014

Таблица 4.7

Для определения граф 7 и 9 поиск осуществляется по графе 3 снизу вверх по таблице. Событие № 5 находится во второй графе снизу, от определяемых работ. По строке найденного события отыскиваем значение графы 9. Оно равно 24. Это число записываем в графу 7 таблицы 4.7 по строкам работ 4—5 и 3—5 (т.к. обе работы входят в одно и то же событие и, следовательно, имеют одну и ту же величину позднего окончания). После этого определяем значение графы 9 по работам 4—5 к 3—5, которое равно результату вычитания из значения графы 7 значения графы 8. Определим значе-

ния ТПОi-j и ТПНi-j для работ 2—3, 1—3 и всех остальных.

61

Таблица 4.8

Событие 3 (графа 3) встречается в графе 2 ниже определяемой работы 2—3 два раза на строках работ 3—4 и 3—5. По этим строкам отыскиваем значение графы 9 и выбираем минимальное (т.е. 14), которое и записываем в графу 7 для работ 2—3 и 1—3 и тотчас определяем значение колонки 9.

Аналогично определяются графы 7 и 9 и по всем остальным работам.

Определим значения графы 10, т.е. величину полного резерва для каждой работы.

62

Таблица 4.9

Значения 10-й графы табл. 4.9 определяются в результате вычитания по каждой строке из значения колонки 7 значения колонки 6. Нули в 1-й колонке находятся на строках критических работ

(0—2; 2—3; 3—5).

Глава 5. СЕТЕВОЕ ПЛАНИРОВАНИЕ ПРИ СЛУЧАЙНЫХ ВРЕМЕНАХ ВЫПОЛНЕНИЯ РАБОТ

5.1. Особенности вероятностных сетевых графиков

До сих пор, рассматривая задачи планирования комплекса работ, мы ограничивались случаем, когда времена выполнения отдельных работ были нам в точности известны заранее (так называемый детерминированный случай). На практике это бывает редко: чаще встречаются случаи, когда фактическое время выполнения

63

работы заранее в точности неизвестно (случайно) и может сильно отклоняться от своего предсказанного значения. Отклонение слу-

чайной величины ti (времени выполнения работы аi) — от ее зара-

нее заданного значения может быть, вообще говоря, в обе стороны — как в большую (опоздание), так и в меньшую (опережение), хотя на практике второе встречается реже первого [2].

Возникают следующие вопросы:

какова вероятность того, что фактическое время выполнения комплекса работ Т не превзойдет заданной величины Tо?

как следует организовать комплекс работ, чтобы величина Т не превзошла заданного То с достаточно высокой вероятностью?

Рассмотрим первый вопрос, как более простой (тем более, что для ответа на второй, прежде всего, надо уметь ответить на пер-

вый). Предположим, что времена выполнения работ t1, t2, ..., tn представляют собой случайные величины с известными законами распределения. Предположим для простоты, что эти случайные величины независимы, и плотности их равны

f1(t), f2(t), ...., fn(t).

Рассматривается функция этих случайных величин — общее

Поставленная задача будет решена, если удастся найти функцию распределения случайной величины Т:

F(t) = P (T<t).

Тогда, подставляя в нее вместо t величину Т0, найдем искомую вероятность.

Функция (5.1) в общем случае является достаточно сложной, так как сам критический путь случаен и зависит от тех значений, кото-

64

рые принимают случайные величины ti — времена выполнения

отдельных работ: при одних значениях ti может быть один критический путь, при других — другой. Однако если ограничиться

только сравнительно малыми отклонениями случайных величин ti

от своих номинальных значений ti(0) (настолько малыми, что критический путь остается тем же), то задача сильно упрощается. Тогда в формуле (5.1) фигурируют только несколько вполне опреде-

лённых случайных величин ti — времен выполнения критических

работ. Закон распределения случайной величины Т представляет собой в этом случае не что иное, как композицию законов распре-

деления случайных величин ti, относящихся к критическим работам.

5.2. Расчет вероятности выполнения комплекса работ в заданный срок

Здесь нам приходит на помощь сама сложность плана и наличие на критическом пути многих работ. Известно, что при сложении достаточно большого числа независимых случайных величин, распределенных по любым законам и сравнимых по порядку дисперсий, закон распределения суммы оказывается близким к нормальному (центральная предельная теорема). Поэтому, если на критическом пути стоит достаточно большое количество работ (скажем, порядка 5 — 6 или более), то на практике можно приближенно

где mti — математическое ожидание времени выполнения i-й работы, а ее среднее квадратичное отклонение

65

где ti — среднее квадратичное отклонение времени выполнения i–й работы.

Таким образом, в данном случае для нахождения закона распределения времени выполнения комплекса работ нет надобности

знать законы распределения fi (t) отдельных времен ti достаточно знать их математические ожидания и средние квадратичные отклонения. Если эти величины известны, вероятность выполнения ком-

плекса в срок Т0 найдется по формуле

Пример 5.1

При выполнении комплекса работ а1, a2,..., an критическими оказываются работы

а1, а2, а3, а4, a5, a6.

времена выполнения которых представляют собой случайные величины

t1, t2, t3, t4, t5, t6.

66

с математическими ожиданиями

mt1 10, mt 2 20, mt 3 10, mt 4 5, mt 5 7, mt 6 10

и средними квадратичными отклонениями;

t1 1, t 2 1, t 3 0,5, t 4 0,3, t5 0,5, t 6 1,

Случайные отклонения времен выполнения работ от их математических ожиданий не меняют критического пути. Задан срок вы-

полнения комплекса T0= 65. Найти вероятность того, что этот срок будет выполнен.

Решение. Имеем

mt = 10 + 20 + 10 + 5 + 7 + 10 = 62,

Ф(1,58) ≈ 0,44, откуда вероятность выполнения комплекса в срок

Р(Т < 65) ≈ 0,94. Если при случайных изменениях времен ti может меняться и сам критический путь, задача вычисления вероят-

ности Р(Т < То) затрудняется. При сравнительно малом числе работ в комплексе эта задача может быть решена аналитическим способом, но при большом их числе расчеты становятся чересчур громоздкими, и на практике оказывается удобнее определять эти вероятности методом Монте-Карло, построив процедуру имитационного моделирования. При этом разыгрываются значения случай-

ных времен ti и для каждой совокупности полученных значений определяется время Т выполнения комплекса работ тем способом,

67

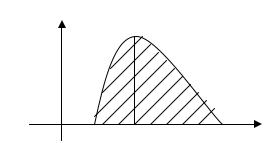
который применяется для неслучайных времен.

fi (t)

Рис. 5.1

Получив достаточно большое число N таких реализаций, мы можем непосредственно найти математическое ожидание, диспер-

сию и среднее квадратичное отклонение случайной величины Т. Что касается закона распределения, то он в большинстве случаев для сложных сетей оказывается близким к нормальному. Поэтому вероятность выполнения плана в срок может быть вычислена по той же формуле (5.4). Если имеются основания считать закон рас-

пределения величины Т не нормальным (так, например, бывает, если рассеивание времени выполнения какой-нибудь одной из критических работ резко превышает рассеивание остальных), то в ка-

честве приближенного значения вероятности Р (Т < То) можно принять частоту этого события в серии реализаций.

Надо заметить, что подобного рода расчеты могут быть только сугубо ориентировочными, так как на практике обычно законы

распределения fi(t) неизвестны, а получение их по статистическим данным затруднительно. В лучшем случае удается указать для

каждого времени ti его наиболее вероятное значение ti*, а также грубо оценить наименьшее («оптимистическое») значение timin и наибольшее («пессимистическое») значение timax (рис. 5.1). Что

касается самого распределения fi(t), то его приходится задавать достаточно произвольно, исходя из умозрительных соображений. Например, то что кривая на рис. 5.1 имеет положительную асим-

68

метрию (более растянута вправо, чем влево) отражает тот общеизвестный факт, что запаздывания по сравнению с плановым сроком могут быть значительно больше, чем опережения.

Рассмотрим более общий пример расчета параметров сетевого графика и расчета вероятности выполнения комплекса работ (проекта) за директивный срок.

Пример 5.2

Технологические связи между работами и временные оценки работ даны в табл. 5.1.

Пользуясь эмпирическими соотношениями (5.5), находим оптимальное время выполнения каждой работы, равное её математическому ожиданию (табл. 5.2).

ti-jож =(3 tijmin + 2tijmax)/5.

69

Таблица 5.2

Пользуясь соотношением (5.6), находим дисперсию каждой работы комплекса

Сетевая модель в соответствии с технологической последовательностью работ (см. табл. 5.1) показана на рис. 5.2.

70