Маслов ИНТРОДУЦТИОН ТО ПХЫСИЦС ОФ СЕЦОНД-ОРДЕР МАГНЕТИЦ 2015

We see that the correlation function falls off exponentially with the distance R between two moments at a characteristic length ξ. This is why

ξ is called the correlation length or the correlation radius. Of fundamental importance is that ξ increases as T decreases and diverges as T → 0.

We turn to the case T < θ. At T = 0 from Eq. (25.20) one has g(R) =

= 1 for any R. At 0 < T < θ and R >> a the expression for g(R) takes the form

where the correlation length ξ is now

It diverges at T → θ, as in the case T > θ.

Finally we note that correlations of magnetic moments are intimately related to their fluctuations, the corresponding operators being

δσiz = σiz − σiz T :

71

26. Heat capacity of a ferromagnet in the Ising model with account for fluctuations

For the contribution from local magnetic moments to the specific heat of a ferromagnet (that is, for the “spin component” of the specific heat) in the mean field approximation we had, see § 20:

This contradicts the experiment that clearly points to the divergence of

Cs at T → θ.

Let us calculate Cs beyond the mean field approximation, with consideration for fluctuations of local magnetic moments, see § 25. By definition,

where Es(T) is a component part of the total internal energy stemming from the subsystem of local magnetic moments. In the Ising model it is equal to the thermodynamic average of the model Hamiltonian, see Eq. (10.6):

(we restrict ourselves to the case of zero magnetic field). Taking Eqs. (25.1) and (25.17) into account, one has

where the function g(q) is temperature dependent.

Let us calculate Cs(T) in the very vicinity of the Curie temperature θ. Making use of expressions for g(q) at T > θ and T < θ, see § 25, evalu-

72

ating the sum over q in Eq. (26.4), and restoring the proper dimensionality, from Eq. (26.2) we have

Two equations (26.5) can be combined into a single one:

The critical exponent α = 0.5 in Eq. (26.6) differs from the experimental value α ≈ 0.1. Note however that accurate experimental determination of α is hampered by the sample inhomogeneity.

27. Magnetic susceptibility of a ferromagnet in the Ising model with account for fluctuations

Our purpose is to calculate the differential magnetic susceptibility

where

73

is the partition function. Taking in Eq. (27.5) the derivatives of both sides with respect to h/T, we have

Now let us calculate the second derivative of Q with respect to h/T making use of Eq. (27.5):

From Eqs. (27.6), (27.8), and (27.9) one has

74

Making use of Eqs. (25.19) and (25.20) we arrive at

Note that both these expressions do not differ from those derived in the mean field approximation, see § 21. Thus, account for fluctuations does not lead to qualitative changes in magnetic susceptibility.

28. Ising model for antiferromagnets. Mean-field approximation. Neél temperature

Up to this point we considered systems with exchange integral Jij > 0. As this takes place, the energy of the system is minimal if the

magnetic moments have the same direction like this ↑↑↑... ↑↑. And

other magnetic moments.

The beginning Hamiltonian will have the same form (see Eq. 10.7)

Considering the mean-field approximation rewrite it in the following way

75

This Hamiltonian has the same form as the Hamiltonian within the Ising model for ferromagnets. Earlier we denoted σjz = x (order parame-

ter). For every j these mean values σjz are identical due to the fact

that in ferromagnetic alignment all magnetic moments have the same direction. For antiferromagnets it will be different. For two neighboring

magnetic moments energy is equal to −J σiz σjz , and it has the minimal

words neighboring magnetic moments have different directions ( ↑↓). This applies for any pair of neighboring magnetic moments. What are our expectations? For one-dimensional case it will be like this:

↑↓↑↓↑↓... ↑↓. For two-dimensional simple cubic lattice the ordering is shown on Fig. 28.1.

↑↓↑↓↑↓↑↓

↓↑↓↑↓↑↓↑

↑↓↑↓↑↓↑↓

↓↑↓↑↓↑↓↑

Fig. 28.1. Magnetic moments ordering in the case of antiferromagnets

So, some atoms have σiz > 0 and other atoms have σiz < 0 , thus

we can not consider siz = x = const for i. Let us divide out system

(the whole lattice) to two sublattices A and B with alternating arrangement of the nodes (see Fig. 28.2).

Such sublattices are called embedded sublattices. Since we consider that Jij = J ≠ 0 only for the neighboring magnetic moments, such divi-

sion on two sublattices suggest that magnetic moments of one sublattice do not interact with each other.

76

σjB z does not depend on the magnetic moment position in B-

sublattice, since all these moments are located in the same environment of magnetic moment from A-sublattice. Analogously

where σjA z = xA is the mean value of magnetic moment projection in

A-sublattice. Therefore we have two different order parameters: xA for A-sublattice and xB B-sublattice. Finally, for our Hamiltonian we obtain

Denote the effective magnetic fields acting on A- and B-sublattices, respectively

As in the case of ferromagnets, we obtain the Hamiltonian of noninteracting magnetic moments placed into the “effective external field” dis-

78

This equation has the same form as for a ferromagnet, but instead of Curie temperature θ one can see another temperature TN . The solution

is already known (see Fig. 28.3).

At T =TN the phase transition is take place, and order parameter be-

comes nonzero. All formulae that we obtained for ferromagnets (see § 14) are valid by replacing the Curie temperature θ on the TN

79

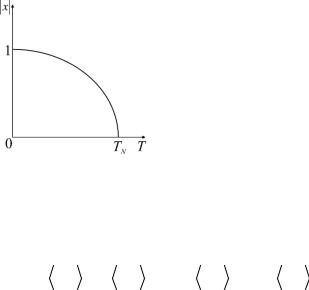
The value TN is called the Neél temperature or transition temperature into antiferromagnetic state.

Fig. 28.3. Parameter order dependence on temperature for antiferromagnets

Since xB = −x , at T =TN the spontaneous magnetization occurs in

every sublattice, but atomic magnetic moments in these sublattices are oppositely directed. Total magnetic moments of A- and B-sublattices are equal in magnitude and opposite in direction. That is why the total magnetization is equal to zero

29. Magnetic susceptibility of the Ising antiferromagnet in the mean-field approximation

As we have seen, the total magnetization in antiferromagnet is equal

80