
Маслов ИНТРОДУЦТИОН ТО ПХЫСИЦС ОФ СЕЦОНД-ОРДЕР МАГНЕТИЦ 2015
.pdf
It is important that Jij falls off exponentially with the distance Ri − Rj between the atoms i and j, being maximum when these atoms
are nearest neighbors. This is why the so called nearest neighbor approximation is of frequent use:
Jij |
J , atoms |
i and |
j |
are nearest neighbors, |
(8.19) |
= |
|
|
|
||
|
0, otherwise. |
|
|
|
|
For different materials the value of J varies widely, being typically in the range 0.001 ÷ 0.1 eV.
9. Interaction of two local magnetic moments
Let us explicitly express the operator ij of the pairwise interaction
U
energy Uij in terms of operators µi and µj of magnetic moments at at-
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
oms i and j. Taking into account |
that (Si S j )= |
4µB2 |
(µi µj ), see |
||||||
Eq. (8.2), from Eqs. (8.13) and (8.15), we have |
|
|
|
|
|||||
|
0 |
Jij |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
||
U ij =Uij − |
2 |
|
(µi µj ), |
|
|
|
(9.1) |
||
where |
|
2µB |
|
|
|
|
|
|
|
|
|
Jij |
|
|
|
|
|
||
U 0 |
= A − |
, |
|
|
|
(9.2) |
|||
|
|
|
|
||||||
ij |
|
ij |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
and the sign of the second term in Eq. (9.1) depends on mutual orientation of the magnetic moments since (µi µj )> 0 in the case that the spin S of two electrons at atoms i and j equals to 1 (“parallel” magnetic moments) and (µi µj )< 0 if S = 0 (“antiparallel” magnetic moments), see §
8. It follows from Eq. (9.1) that for the magnetic moments of i-th and j- th atoms it is energetically favorable to be oriented in one direction if Jij > 0 and in opposite directions if Jij < 0.
In the case that Jij > 0 for any pair of atoms (i, j) in the sample, the
total energy of the system is minimum when all magnetic moments are unidirectional. This is the ferromagnetic ordering. Next, as long as 21
Jij < 0 for any two nearest atoms and negligibly small otherwise, the total energy is minimum when any two nearest moments are oppositely directed. Such a type of ordering is referred to as antiferromagnetic. It is reminiscent of a checkerboard order. In the general case, the sign of Jij may vary with the distance between the atoms i and j, resulting in rather complex magnetic textures, neither ferromagnetic nor antiferromagnetic.
It should be pointed out that the very possibility of one or another type of magnetic order to take place in a given solid strongly depends on its crystal structure. For example, the antiferromagnetic ordering cannot occur on a triangular lattice because of frustration. Besides, in anisotropic crystals different types of magnetic order may exist along different crystal axes.
10. Heisenberg model and Ising model
Up to now we have discussed the interaction between two local
magnetic moments and derived the operator ij of the corresponding
U
interaction energy, see Eqs. (9.1) and (9.2). We now turn to the macroscopic system of N 1 moments. With consideration for an external
magnetic field H the Hamiltonian is
|
1 |
/ |
|
|
|
|
|
|
|
|
(10.1) |
||
H = |
|
∑ U ij − H ∑µ, |
||||
|
2 i, j |
|
|
i |
|
|
where the sum over both i and j is from 1 to N, the prime implies that
i≠ j, and we took into account that U ji =U ij . For the sake of conven-
ience let us, first, introduce the operators σi = µi  µB and, second, redefine the exchange integral Jij → 2Jij in Eq. (9.1), so that
µB and, second, redefine the exchange integral Jij → 2Jij in Eq. (9.1), so that
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
(10.2) |
|||
|
U ij =Uij |
− Jij (σi σj ) , |
|
||||||
and Eq. (10.1) becomes |
|
1 |
|
|
|
|
|
|
|
|
|
|
/ |
|
|
||||
|
|
|
|
|
|
|
|
(10.3) |
|
H = − |
|
∑ Jij (σi σj ) − h∑σi , |
|||||||
|
|
2 i, j |
|
|
|
i |
|
|
|
22

where we measured the energy from 1 |
∑/ Uij0 and used the designation |
|||||||||||
|
|
|
|
|
|
2 i, j |
|
|
||||
h = µB H . Note that the operators |
|
have two eigenstates, |
|
↑ and |
||||||||
|
||||||||||||
σiz |
|
|||||||||||
|
↓ , with eigenvalues +1 and –1 respectively: |
|
|
|||||||||
|
|
|
||||||||||
|
|
|
↑ = |
|
↑ , |
|
|
↓ = − |
|
↓ , |
(10.4) |
|
|
|
|
|
|
||||||||
|
σiz |
|
|
σiz |
|
|
||||||
see § 4.
The Hamiltonian (10.3) is referred to as the Hamiltonian of the isotropic Heisenberg model. The term “isotropic” points to equal strength of interaction between the components of magnetic moments along x, y,
and z axes: Jij (σi σj ) = Jij σix σjx + Jij σiy σjy + Jij σiz σjz . In general, how-
ever, this is not the case because of the crystal field anisotropy, and the Hamiltonian has the form
|
1 |
∑ |
|
Jij |
|
|
|
|
|
|
|
|
|
|
H = − |
/ |
σix σjx +Jij |
σiy σjy + Jij |
σiz σjz − h |
∑σi . (10.5) |
|||||||||
|
|
xx |
|
|
yy |
|
|
zz |
|
|
|
|
||
|
2 i, j |
|
|
|
|
|
|
|
|
|
|
|
i |
|
This the Hamiltonian of the anisotropic Heisenberg model. For the special case of Jijxx = Jijyy = Jijzz it reduces to Eq. (10.3). For another limiting
case Jijxx , Jijyy << Jijzz ≡ Jij we have the Hamiltonian of the Ising model:
|
|
1 |
|
/ |
|
|
|
|
|
|
|
|
∑ |
|
|
|
|
(10.6) |
|||
H = − |
|
|
Jij σiz σjz − h |
∑σi . |
||||||
|
|
2 i, j |
|
|
|
|
i |
H = Hez , i.e., |
h = hez , |
|
Usually this model is simplified further taking |
||||||||||
where h = µBH: |
|
1 |
|
|
|
|
|
|
|
|
|
= − |
∑ |
/ |
|
|
|
|
|
(10.7) |
|
H |
|
|
Jij σiz σjz − h∑σiz . |
|||||||
|
|
2 i, j |
|
|
|
|
i |
|
|
|
This is the Hamiltonian we shall study in what follows.
Contrary to the case of noninteracting magnetic moments, there is now the term that accounts for interaction of moments to one another.
As before, our objective is to find magnetization M as a function of T and H.Inasmuch as H = Hez , we have M = Mez , where
23

|
1 |
N |
|
|
µB |
N |
|
|
|
M = |
|
∑ |
µiz |
= |
|
∑ |
σiz . |
(10.8) |
|
V |
V |
||||||||
|
i=1 |
|
T |
i=1 |
T |
|
Since all magnetic moments are alike, the value of  σiz
σiz  T does not depend on i, and hence
T does not depend on i, and hence
M = |
µB N |
|
, |
(10.9) |
V |
σiz T |
where one can take  σiz
σiz  T for any one of N moments. In general this
T for any one of N moments. In general this
problem has no exact analytic solution, and one must either resort to numerical calculations or make use of one or another approximation.
11. Mean-field approximation in the Ising model
As mentioned above, in the general case the exact analytic solution of Ising model with interactions can not be found. However if we repre-
sent Hamiltonian (10.7) as the sum of terms depending only on the σiz , the problem will be solved. Further we shall use the approach that make
|
|
|
|
|
|
|
|
|
|
|
the term σiz σjz linear in σiz . |
|
|
|
|
|
|
). Conse- |
|||
Rewrite |
|
as |
|
|
|
|
|
|
|
|
σiz σjz |
(σiz − σiz |
+ σiz |
)(σjz − σjz |
+ σjz |
||||||
quently |
|
|
|
|
|
|
|
)+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
σiz |
σjz |
= σiz |
σjz |
+ σiz |
(σjz − σjz |
), |
(11.1) |
||
|
|
|
|
|
|
|
|
|
||
|
|
|
||||||||
|
+ σjz |
(σiz − σiz |
)+(σiz − σiz |
)(σjz − σjz |
|
|||||
where  σiz
σiz  and
and  σjz
σjz  are the mean values of the magnetic moments,
are the mean values of the magnetic moments,
σiz −  σiz
σiz  and σjz −
and σjz −  σjz
σjz  are the operators of magnetic moments fluc-
are the operators of magnetic moments fluc-
tuations (they define the difference between true moments and the mean value). One can see three different terms in the sum written above: terms that do not depend on fluctuations, terms that depend linearly on fluctuations, and terms that depend quadratically on fluctuations. In other words, we can present the interaction of two magnetic moments as a
24

sum of three types of interactions (for each pair of magnetic moments): interaction of mean magnetic moments with each other, interaction of mean magnetic moments with fluctuations, and interaction of fluctua-
tions with each other. |
|
|
|
|
|
|
|||||||
|
Let |
us |
|
|
consider |
|
that |
fluctuations |
are |
small, |
i.e., |
||
|
|
|
) |
2 |
|
|
|
|
1. Since we consider that fluctuations are |
||||
|
|
|
|
||||||||||
|
(σiz − σiz |
|
|
|
σiz |
|
|||||||
small, we neglect the terms in Hamiltonian that depend quadratically on fluctuations, but leave terms that depend linearly on fluctuations
σiz σjz ≈  σiz
σiz 
 σjz
σjz  +
+  σiz
σiz  (σjz −
(σjz −  σjz
σjz  )+
)+  σjz
σjz  (σiz −
(σiz −  σiz
σiz  )=
)=
= σiz  σjz
σjz  + σjz
+ σjz  σiz
σiz  −
−  σiz
σiz 
 σjz
σjz  .
.
(11.2)
This approach is called the mean-field approximation. Taking into account the approximation used (for each pair of magnetic moments) rewrite the Hamiltonian of the Ising model
|
1 |
∑ |
/ |
|
|
|
|
|
|
|
(11.3) |
H ≈ − |
|
|
Jij (σiz |
σjz |
+ σjz |
σiz |
− σiz |
σjz |
)− h∑σiz . |
||
|
2 i, j |
|
|
|
|
|
|
|
i |
|
|
Considering that Jij = J (Ri − Rj ), and consequently Jij = J ji , replacing i ↔ j , we require for the second term
∑ |
/ |
|
|
= ∑ |
/ |
|
|
= ∑ |
/ |
|
|
, |
(11.4) |
|
Jij σjz |
σiz |
|
J ji σiz |
σjz |
|
Jij σiz |
σjz |
|||||
i, j |
|
|
|
i, j |
|
|
|
i, j |
|
|
|
|
|
that is equal to the first term. The third term is a constant
|
|
|
|
|
|
|
|
2 |
|
|
|
|
1 |
∑ |
/ |
Jij |
|
|
|
σz |
|
∑ |
/ |
Jij ≡ E0′. |
(11.5) |
|
|
σiz |
σjz |
= |
2 |
|
|
|||||
2 i, j |
|
|
|
|
|
|
i, j |
|
|
|
||
Therefore, we can write down the Hamiltonian of the Ising model in the following form
|
/ |
|
|
|
(11.6) |
H ≈ E0′ −∑ |
|
Jij σiz |
σjz |
−h∑σiz . |
|
i, j |
|
|
|
i |
|
Considering that our system is homogeneous (i.e., it is free from intersti-
tial magnetic moments), |
|
does not depend on j . Therefore, we |
σjz |
25
can denote |
|
as |
|
, the same for all j . Then the term |
σjz |
σz |
∑ |
/ |
|
|
|
|
|
in |
the |
|
Hamiltonian |
|
takes |
the |
form |
||
|
Jij σiz |
σjz |
|
|
|
|||||||||||
i, j |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∑ |
/ |
|
|
|
N |
N |
|
Recall that Jij |
= J (Ri − Rj )= J (Rl ), |
|||||
σz |
|
Jij σiz |
= σz ∑∑Jij σiz . |
|||||||||||||
|
|
i, j |
|
|
|
|
i=1 |
j≠i |
|
|
|
|
|
|
|
|
where Rl |
= Ri |
− Rj |
is the vector drawn from j-th magnetic moment to i- |
|||||||||||||
th, and convert the sum ∑ to ∑ in the interaction term |
|
|||||||||||||||
|
|
|
|
|
|
|
|
j≠i |
l ≠0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
N N |
|
|
|
|
N |
/ |
|
|
(11.7) |
|
|
|
|
|
|
σz ∑∑J |
(Ri − Rj )σiz = σz |
∑∑ |
|
J (Rl |
)σiz , |
||||||
|
|
|
|
|
|
i=1 |
j≠i |
|
|
|
|
i=1 l |
|
|
|
|
where ∑/ is the sum for all vectors Rl |
that drawn from arbitrary atom |
|||||||||||||||
|
|
|
l |
|
|
|
|
|
|
|
|
|
|
|
|
|
(magnetic moment) to all other atoms (magnetic moments), the prime implies that Rl ≠ 0. This sum is the same for every atom, since we con-
sider that all atoms (magnetic moments) located periodically, i.e., they form the crystal. Thus, the interaction term takes the following form
|
∑ |
/ |
|
N |
|
where ∑ |
/ |
J (Rl ) is the certain characteristic en- |
σz |
|
J (Rl )∑σiz , |
|
|||||
|
l |
|
|
i=1 |
|
l |
|
|
ergy (sum of the energies of exchange interactions of randomly selected atom with all other atoms). Taking into account that J (Rl ) falls off ex-
ponentially as the Rl increases, denote the J (Rl )= J for the nearest neighbors and considering that J (Rl )= 0 for other atoms, we obtain ∑/ J (Rl )≈ zJ, where z is the number of nearest neighbors of each
l |
|
atom (magnetic moment). Since J = (0.001÷0.1) eV, zJ |
may take the |
sufficiently large values zJ = (0.1÷1) eV. Denote this energy as |
|
∑/ J (Rl )= kBθ, |
(11.8) |
l |
|
26

where θ is the some characteristic temperature (next, we shall omit the Boltzmann constant).
Thus, taking into account the notation introduced, we can write down the Hamiltonian of the Ising model in the following form
|
|
N |
N |
= E0′ |
|
N |
(11.9) |
H = E0′ − |
σz |
θ∑σiz − h∑σiz |
−(θ σz |
+ h)∑σiz . |
|||
|
|
i=1 |
i=1 |
|
|
i=1 |
|
Denote the “effective field” heff |
|
|
. So, the Hamiltonian of the |
||||
= h + θ σz |
|||||||
Ising model can be described as |
N |
|
|
|
|||
|
|
|
E0′ − heff |
|
|
(11.10) |
|
|
|
H = |
∑σiz . |
|
|||
i=1
The main differences between this Hamiltonian and the Hamiltonian
|
N |
are the appearance |
of noniteracting magnetic moments H0 |
= −h∑σiz |
i=1
of the constant E0′ (note that E0′ does not affect on the  σz
σz  calculation)
calculation)
and the field h substituted by the “effective field” heff = h + θ σz
σz  .
.
Finally, in the mean-field approximation system of interacting magnetic moments can be approximately described as the system of nonin-
teracting magnetic moments placed into the “effective field” heff ≠ h.
12. Curie-Weiss equation and Curie-Weiss law
We now apply the mean-field approximation to the system of magnetic moments with Jij ≥ 0 (i, j) . In particular, we assume Jij = J
for the nearest neighbors and Jij = 0 for other atomic pairs. Magnetization of such system (projection on the z-axis) equals to
|
|
|
|
N |
|
|
|
|
|
|
|
|
|
M = |
µz |
= |
NµB x |
, |
(12.1) |
||
|
|
|
|
V |
V |
|||||
|
|
|
|
|
|
|||||
where |
µB . The parameter x does not depend on i , |
|||||||||
x = σz |
= µz |
|||||||||
−1≤ x ≤1, and x = 0 in the case of  µz
µz  = 0. Let us find x = x(T, H ).
= 0. Let us find x = x(T, H ).
27

Recall that the Hamiltonian of the Ising model in the mean-field approximation is
|
N |
(12.2) |
H |
= E0′ − heff ∑σiz . |
i=1
N
Constant E0′ does not affect on the  σz
σz  calculation, term −heff ∑σiz is
calculation, term −heff ∑σiz is
i=1
the operators sum of the interaction between each magnetic moment and “effective field”. In other words, in our approximation magnetic moments do not depend on each other, but they located in the “effective
field” heff . Therefore, the value  σz
σz  for arbitrary magnetic moment can be obtained in terms of single magnetic moment located in the field
for arbitrary magnetic moment can be obtained in terms of single magnetic moment located in the field
heff . Hamiltonian for the single moment located in the field
|
|
|
|
|
can be obtained as follows |
|||||||||||||
H |
= −heff σz . Therefore |
σz |
||||||||||||||||
|
|
|
|
|
−H T |
|
|
|
|
|
|
) |
|
|||||
|
|
|
Tr (σze |
|
|
|
) |
|
|
Tr (σze |
|
|
||||||
|
|
|
|
ˆ |
|
|
heff σz T |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
σz = |
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
= |
||
|
|
|
Tr |
(e−H T ) |
|
|
|
Tr (eheff σz |
T ) |
|
|
|||||||
|
|
eheff |
T |
−e−heff |
T |
|
heff |
|
|
|
||||||||
|
= |
|
|
|
|
|
|
|
= tanh |
|
|
|
. |
|
|
|||
|
|
h |
T |
+ e |
−h |
T |
|
T |
|
|
||||||||
|
|
e eff |
|
|
eff |
|
|
|
|
|
|
|
||||||
heff is
(12.3)
Recall that the heff = h + θ σz
σz  ≡ h + θx . Therefore the Eq. (12.3) takes the form
≡ h + θx . Therefore the Eq. (12.3) takes the form
h + θx |
(12.4) |
||
x = tanh |
T |
|
|
|
|
|
|
Such dependence of x is referred to as Curie-Weiss equation.
Let us find the magnetization and magnetic susceptibility at high
temperatures T h + xθ . At high temperatures |
h + θx |
→ |
h + θx |
, |
||||
tanh |
T |
|
T |
|||||
|
|
|
|
|
|
|
||
therefore |
x ≈ h + θx |
. Finally, we obtain |
|
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
28
x = |
|
|
h |
|
|
|
= |
|
µB H |
, |
|
|
(12.5) |
||||||||
|
T −θ |
|
T −θ |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
M = |
Nµ |
B |
x |
= |
|
Nµ2 |
H |
, |
(12.6) |
||||||||||||
|
|
|
|
|
|
|
|
|
|
B |
|
|
|
|
|||||||
|
|
V |
|
|
|
|
V |
|
T |
−θ |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
χ = |
M |
|
= |
|
NµB2 |
1 |
|
. |
|
(12.7) |
|||||||||||
H |
|
|
|
V |
|
|
|
T −θ |
|
||||||||||||
The latter temperature dependence of χ is referred to as Curie-Weiss law. Note that if the exchange interaction is absent ( Jij = 0 ), then
θ = 0 , so, we obtain the Curie law. The value θ is called the Curie temperature.
13. Ferromagnetic transition in the Ising model. Curie temperature. Order parameter
In the previous paragraph we have shown that at high temperatures
magnetic susceptibility χ = |
NµB2 |
1 |
. One can see that the value of χ |
||||||||||||
|
V |
|
|
T −θ |
|||||||||||
diverges at T → ∞. |
This is due to a violation of the conditions of ap- |
||||||||||||||
plicability |
of our solution. Indeed, we obtained that x = |
µB H |
, i.e., |
||||||||||||
T −θ |
|||||||||||||||
|
T → θ. |
|
|
|
|
|
|
|
|
|
|
|
|||
x → ∞ at |
Therefore |
the |
condition |
T h + xθ |
is |
not |
valid. |
||||||||
However, |
one can |
see that |
some |
“critical” |
temperature |
θ |
exists at |
||||||||
which something happens. Maybe it is a transition to ferromagnetic state? Let us study the Curie-Weiss equation in more detail.
Consider the h = 0 in the Curie-Weiss equation, thus the latter takes the following form
|
θ |
(13.1) |
|
x = tanh x |
|
. |
|
|
|||
|
T |
|
|
This equation can not be solved analytically. We shall try to solve it graphically. From the Fig. 13.1 and 13.2 one can see that at T > θ the Curie-Weiss equation has only one solution ( x = 0 ), but at T < θ it has three solutions ( x = 0; x ≠ 0 ).
29
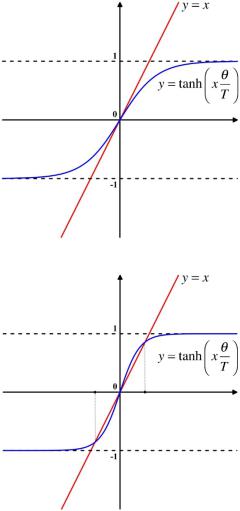
Fig. 13.1. Graphic solution of the Curie-Weiss equation at T > θ
Fig. 13.2. Graphic solution of the Curie-Weiss equation at T < θ
Thus, the main conclusion is that at T = θ = ∑/ J (Rl )≈ (10 ÷1000) K
l
the phase transition into ferromagnetic state occurs, i.e., at T > θ and H = 0 we obtain M = 0 (paramagnetic phase), and at T < θ and H = 0
30
