Пособие кур_раб_2211

Продолжение табл. 4.5

11

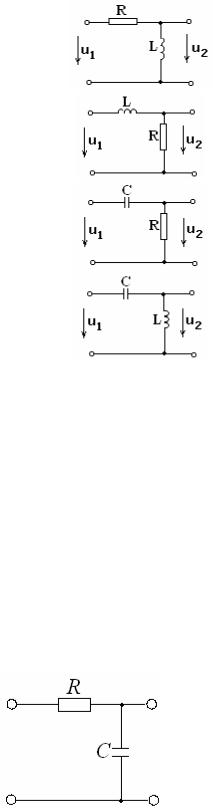
Окончание табл. 4.5

Номер варианта схемы соответствует сумме последних двух цифр шифра в зачетной книжке студента (если сумма равна нулю, выбирается вариант № 19).

Для входного воздействия и найденного отклика построить графики зависимостей u t ,i t .

Импульсные характеристики или переходные функции цепи рассчитать самостоятельно, если выражения для них не приведены в таблице 4.6.

12

Продолжение табл. 4.6

13

Окончание табл. 4.6

hu(t) 0 sin 0 t;

hi(t) 1sin 0t

Студентам заочной формы обучения при выполнении третьего раздела курсовой работы необходимо определить частоты, на которых выполняются условия резонанса токов и резонанса напряжений для короткозамкнутого отрезка кабеля без потерь длиной l с первичными параметрами L0,C0. Найти входное сопротивление кабеля на частоте f 100 МГц. Значения L0,C0,l выбрать из таблицы 4.7. Кроме того, определить наименьшую длину разомкнутого отрезка кабеля без потерь с первичными параметрами L0,C0, входное сопротивление которого на частоте 100 МГц эквивалентно емкости С. Значения параметров L0,C0,C выбрать из таблицы

4.8.

Номер варианта задания соответствует последней цифре шифра зачетной книжки студента.

14

5 МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ КУРСОВОЙ РАБОТЫ

5.1 Классический метод анализа переходных процессов

Классический метод анализа переходных процессов в электрической цепи основан на использовании неоднородных линейных дифференциальных уравнений с постоянными коэффициентами, выражающих законы Кирхгофа [3]:

15

Решение уравнения (5.1) представляет собой сумму общего решения однородного уравнения:

и частного решения неоднородного уравнения (5.1). Общее решение уравнения (5.2) описывает свободную составляющую переходного процесса xсв t , частное решение уравнения (5.1) – принужденную составляющую xпр t . Таким образом, переходной процесс складывается из свободной и принужденной составляющих:

x t xсв t xпр t .

Свободная составляющая переходного процесса определяется только свойствами цепи и не зависит от вида входного воздействия. Для ее нахождения записывают и решают характеристическое уравнение для дифференциального уравнения (5.2):

Если p1,p2 ,...,pn – корни характеристического уравнения (5.3), причем, среди них нет равных, то решение уравнения (5.2) запишется в виде:

где А1,…,Аn – постоянные интегрирования, определяемые начальными условиями.

Из выражения (5.4) видно, что свободная составляющая состоит из n линейно независимых слагаемых.

Если k корней характеристического уравнения равны между собой:

p1 p2 ... pk p,

то решение однородного уравнения запишется в виде:

Решение (5.5) справедливо и в случае k=n.

Если одна или несколько пар корней уравнения (5.3) является комплексно сопряженными и не равны друг другу:

то решение xсв (t)будет содержать слагаемые вида:

xсвk xсвk 1 Ak e bktsin(щkt шk ),

xсвл 2 xсвk 3 Ak 2 e bk 2tsin(щk 2t шk 2),

16

где щk ,щk 2 иbk ,bk 2 – собственные частоты и собственные затухания со-

ставляющих, определяемые параметрами цепи.

Общее решение xсв(t) будет иметь в этом случае следующий вид:

xсв t A1ep1t A2ep2t ... Ak 1epk 1t Ake pkt sin kt k

Ak 2epk 2t sin k 2t k 2 Ak 4epk 4t ... Anepnt . (5.6)

Величины Аk, Ak+2 и k , k 2 находятся, исходя из начальных условий.

Если какая-либо пара комплексно сопряженных корней имеет кратность k (k пар комплексно сопряженных корней равны между собой), то соответствующие k пар членов в формуле (5.4) заменяются слагаемыми

e bt c1 c2t ... cktk 1 cosщt b1 b2t ... bktk 1 sinщt ,

где постоянные интегрирования с1, с2,…,сk и b1, b2,…,bk определяются из начальных условий.

Принужденная составляющая xпр t определяется как отклик цепи на входное воздействие при t , когда свободная составляющая xсв t прак-

тически затухает. Вид принужденной составляющей xпр t определяется входным воздействием y t . В том частном случае, когда y t есть величи-

на постоянная, равная U0 , частное решение находится из равенства:

(5.7)

Для определения частного решения уравнения (5.1) при других видах входного воздействия y t необходимо воспользоваться известными мето-

дами решения неоднородных линейных дифференциальных уравнений с постоянными коэффициентами [6].

Постоянные интегрирования определяются после нахождения частного решения уравнения (5.1) и общего решения уравнения (5.2) по известным начальным условиям. В качестве независимых начальных условий используются величины токов индуктивностей и напряжений на емкостях в момент времени t=0, т.е. iL 0 иuc 0 . В качестве зависимых началь-

ных условий используются значения производных токов и напряжений в момент времени t=0.

5.1.1 Примеры расчёта переходных процессов классическим методом

Пример первый.

Электрическая цепь, показанная на рисунке 4.1, включается на постоянное напряжение.

17

Для переходного процесса, возникающего в заданной электрической цепи при замыкании рубильника S, определить ток в неразветвлённой части цепи и переходное напряжение uC (t) на зажимах конденсатора при нулевых начальных условиях. Параметры цепи: U0=400 В, R=50 Ом, L=1000 мГн, С=50 мкФ.

Расчёт На основании первого и второго законов Кирхгофа запишем систему

уравнений для режима цепи при подключении источника постоянного напряжения величиной U0.

Дифференцируя уравнение (5.9), находим:

Учитывая уравнение (5.10), получим:

Подставляя найденное значение i2 в уравнение (5.8), получим следующее уравнение для определения тока i1(t):

Для рассматриваемого переходного процесса дифференциальное уравнение свободного режима имеет вид:

Характеристическое уравнение свободного режима электрической цепи запишется в виде:

Найдём корни уравнения (5.15) по формуле:

18

Подставив численные значения R, L, C, получим:

p1 -58,58(c 1), p2 -341,42(c 1).

Корни уравнения (5.16) действительны и различны, поэтому свободная составляющая тока i1св(t) будет равна:

Принуждённую составляющую i1пр(t) определим, воспользовавшись выражением:

Откуда:

i1пр U0 400 8 (А)

R 50

Суммируя полученные решения, получим следующее выражение для тока i1:

Найдём эти величины, воспользовавшись независимыми начальными условиями:

19

Подставляя численные значения, имеем:

Для определения постоянных интегрирования А1, А2 найдём i1 0 и

Учитывая начальные условия, получим систему уравнений для определения А1, А2:

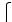8 A1 A2 8,

(5.25)

-58,58A1 -341,42A2 3,2 103.

Решая систему, находим А1=-11,314 и А2=11,314. Окончательно выражение для тока i1(t) запишется в виде:

Графики изменения токов i1(t), i1пр(t), i1св(t) представлены на рисунке

5.1.

20