Вопрос 32. Интегральные законы Ома.

Рассмотрим движение зарядов внутри проводника – согласно T6, элементарная работа плотности тока перемещению заряда (∂A = qρ₀jdr)

Эту же работу можно рассматривать, как работу электрического тока ( )

Как и любое силовое поле, электрическое поле можно разделить на две составляющие – потенциальное и не потенциальное ( )

Тогда интегрируя выражения для работы, можно получить:

Т10 - Интегральный закон Ома для участка цепи,

содержащего ЭДС.

Величину – называют напряжением на участке цепи, соответственно, произведение IR₁₂ – называют падением напряжения на сопротивлении R₁₂ .

Здесь обозначено:

Т11 - ЭДС; - сопротивление.

Частные случаи:

Для замкнутого проводника, очевидно , и мы получаем интегральный закон Ома для замкнутой цепи

Т13

Здесь R₁₂=R₀+r, причем R₀ – сопротивление внешней цепи, r – (внутреннее) сопротивление ЭДС, ε – алгебраическая сумма всех ЭДС в цепи.

Если ε₁₂=0 – то получается интегральный закон Ома для участка цепи, не содержащего ЭДС.

Т14

Отметим, что напряжение на участке цепи , в общем случае, не равно падению напряжения IR на сопротивление R (смотри формулу Т10).

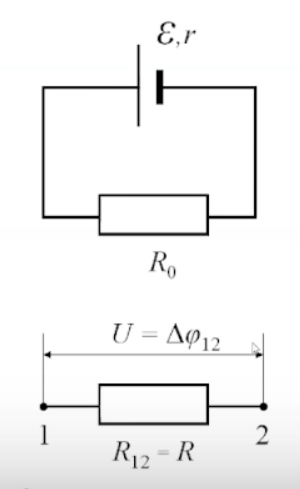Приложение 1.

33. Закон Ома в дифференциальной форме

Элементарная работа по перемещению зарядов внутри проводника может быть выражена через плотность тока:

Эту же работу можно рассматривать, как работу электрического поля:

В силу равенства элементарных работ плотности тока и электрического поля:

Закон Ома в дифференциальной форме:

, где – удельная проводимость

Плотность тока в любой точке проводника пропорциональна напряженности электрического поля в этой точке

34. Тепловое действие тока (закон Джоуля-Ленца в дифференциальной и интегральной формах)

П о формулам для мощности тока N и удельной мощности тока ω с учетом закона Ома в дифференциальной форме несложно получить

- закон Джоуля-Ленца в дифференциальной форме

Формулировка:

Удельная мощность тока, выделяемая в окрестности данной точки проводника (т.е. в элементарном объеме с радиус-вектором r) пропорциональна квадрату плотности тока в этой точке.

ДАЛЕЕ ВЫВОД:

Формула для удельной мощности тока ω с помощью з-на Ома в дифф.форме принимает вид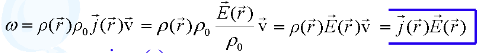

Если учесть, что j = ρ(r)v то последнюю формулу можно записать еще и так

В оспользуемся еще раз законом Ома

П о смыслу, удельная мощность – это мощность, выделяемая в единицу времени dt в единичном объеме dV – следовательно, dQ = ωdVdt – элементарной количество тепла, выделяемое в объеме dV

Интегрируя, получим Закон Джоуля-Ленца в интегральной форме

Формулировка:

Количество тепла Q, выделяемое в проводнике (во всем его объеме) по которому течет постоянный ток силой I за время t пропорционально разности потенциалов в Δϕ₁₂ на концах проводника.

Д АЛЕЕ ВЫВОД:

Нам нужно вычислить интеграл где

П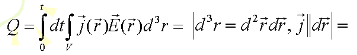 олучаем

Правило Кирхгофа

1. В каждом проводнике произвольно (и независимо от остальных) выбирают направление вектора плотности тока

2. Любая сложная электрическая цепь разбивается на отдельные замкнутые участки, называемые контурами

• в каждом контуре произвольно (и независимо от остальных контуров) выбирают направление обхода

• в каждом контуре, содержащем ЭДС, выбирают ее положительное направление – например, от плюса к минусу (либо наоборот - но во всех контурах одинаково)

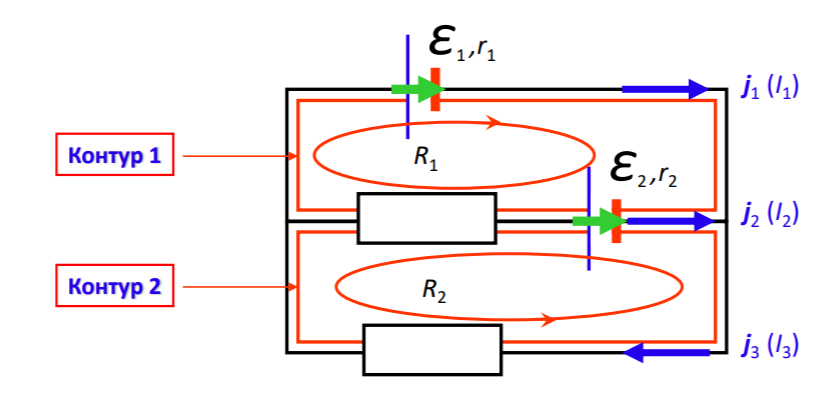
3. Любая точка электрической цепи, в которой сходится более 2 (двух) проводников, называется узлом 1 закон Кирхгофа: