экзамены и коллоквиумы / Вопросы к коллоквиуму 3

Для зарядов с непрерывным распределением по поверхности:

4. О. Дифференциальные операторы (оператора V (набла), дивергенция функции divF, ротор функции rotF)

Оператор набла 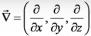формальный вектор, компоненты которого - некоторые объекты, желающие взять частную производную от функции.

5. О. Безвихревой характер электростатического поля

Вихревое поле – векторное поле F, ротор которого не равен 0 (нет источников, силовые линии замкнуты на себя)

Электростатическое поле - безвихревое – ротор напряженности равен 0

Силовые линии никогда не замыкаются сами на себя, начинаются или заканчиваются на заряде.

6. Поток вектора напряженности

7. Теорема Гаусса (в том числе - для точечного заряда)

О – (вакуум и диэлектрик, интегральная и дифференциальная формы)

Для точечного заряда:

Т.к.

Элементарный объемный (телесный) угол –

Тогда Т. Гаусса для точечного заряда:

Элементарный поток dФ вектора напряженности электростатического поля Е точечного заряда q в заданный телесный угол dΩ зависит только от величины заряда q

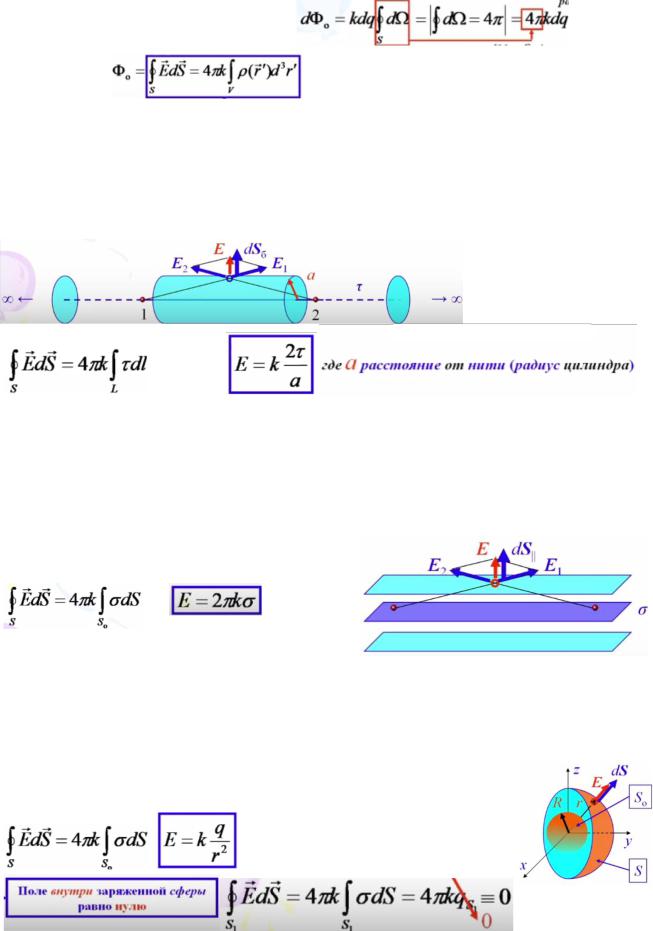
Т. Гаусса для произвольно заряженного тела тела – поток вектора напряженности электростатического поля через замкнутую поверхность, охватывающую произвольное заряженное тело, пропорционален заряду тела.

Для любого элементарного заряда внутри тела 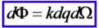, причем 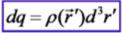Окружим тело замкнутой поверхностью, тогда

Интегрируя по всему объему тела получим: Теорема гаусса –

8. Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити Линейная плотность заряда на нити постоянна

Эквипотенциальная поверхность для нити – коаксиальная цилиндрическая поверхность, с заглушками на бесконечности.

Для любой точки боковой поверхности цилиндра вектор напряженности Е параллелен вектору нормали к боковой поверхности dSб

Тогда т. Гаусса для нити:

9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости

Поверхностная плотность заряда на плоскости постоянна Эквипотенциальная поверхность для плоскости – поверхность параллелепипеда

Любая бесконечная плоскость – множество бесконечных прямых -» для любой точки поверхностей параллелепипеда, параллельных заряженной плоскости, вектор напряженности Е параллелен вектору нормали к поверхности dS

Тогда т. Гаусса для плоскости:

Напряженность поля над и под плоскостью одинаковы

10. Т. Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности

Поверхностная плотность заряда на сфере постоянна Эквипотенциальная поверхность для сферической плоскости – сфера

Для любой т. поверхности сферы S вектор напряженности Е параллелен вектору нормали к поверхности dS

Тогда т. Гаусса для сферической равномерно заряженной поверхности:

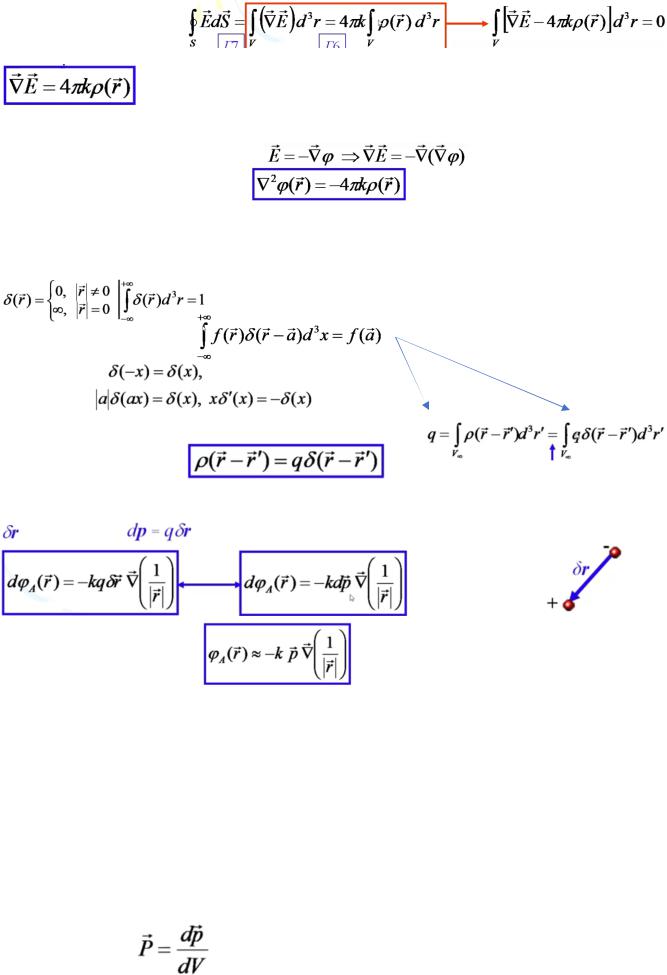
11. Теорема Гаусса в дифференциальной форме (вакуум)

По теореме Остроградского:

Т. Гаусса в диф. форме:

Дивергенция в-ра напряженности электрост. Поля в любой т. пространства пропорциональна плотности заряда в этой точке

12. Уравнение Пуассона (вакуум)

Электрост-е поле всегда потенциально -»

Тогда из т. Гаусса - Уравнение Пуассона

13. Плотность заряда для точечного заряда (δ – функция Дирака)

δ – функция:

В т., где заряда нет – плотность заряда = 0, в т., где заряд есть – плотность равна бесконечности.

Важнейшее св-во δ – функции:

Полезный св-ва:

Величина точечного заряда через плотность заряда и δ – функцию Тогда для точечного заряда

14. Поле диполя

Диполе – система сост. из 2х точечных зарядов разных знаков, наход-ся на небольшом расстоянии 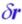- плечо диполя, - элем-й дипольный момент

Для неэлементарного диполя:

15. Диэлектрики и вектор поляризации

Диэлектрик – любое в-во, не имеющее собственных свободных носителей тока.

Полярные(гидрофильные) – вода – прямо в пространстве разделены заряды разного знака, имеют собственный дипольный момент Неполярные(гидрофобные) – кислород, парафин – заряды не разделены и диполь не образуют.

Во внешнем силовом поле диэлектрик поляризуется.

-в полярном дипольные молекулы выстраиваются вдоль силовых линий поля

-в неполярном молекулы поляризуются – вытягиваются вдоль силовых линий, образуя диполи В результате на поверхности диэлектрика появляется эл. заряд.

Вектор поляризации – в-р, характеризующий дипольный момент диэлектрика в каждой точке внутри диэлектрика.

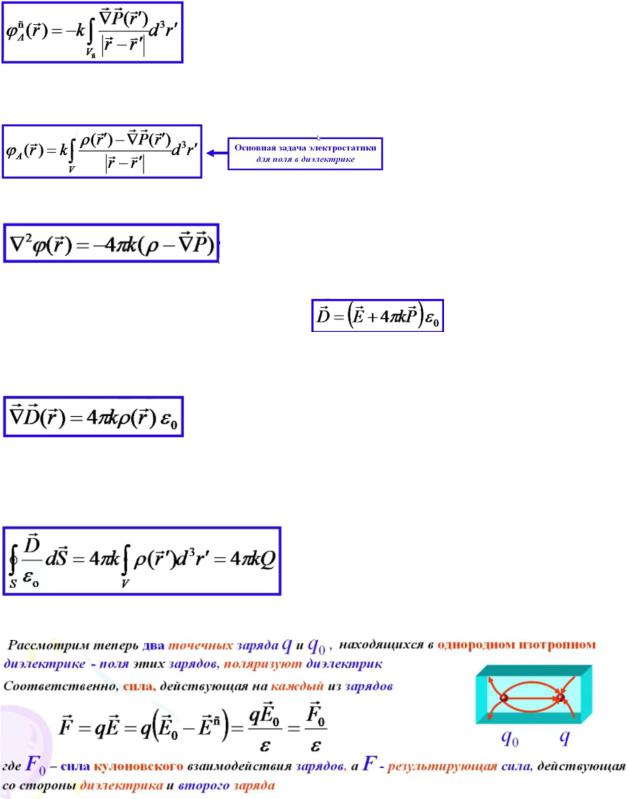
Л4.16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды)

Поле, создаваемое всем объемом диэлектрика, описывает потенциал электростатического поля связанных зарядов Истинные и связанные заряды - возникающие за счет поляризации диэлектрика, т.е. наведенные

в диэлектрике внешним полем – не могут свободно двигаться

Плотность связанных зарядов -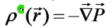

Результирующее электростатическое поле истинных и связанных зарядов:

17.Уравнение Пуассона для поля в диэлектрике

18.Теорема Гаусса для поля в диэлектрике (+вектор электрического смещения)

Вектор эл-го смещения (в-р индукции)

Т. Гаусса для поля в диэлектрике:

Дивергенция вектора электрического смещения электростатического поля в любой т. пространства пропорциональна плотности истинных зарядов в этой точке

19. Т. Гаусса для поля в диэлектрике (интегральная форма)

Поток вектора индукции электростатического поля через замкнутую поверхность, охватывающую произвольно заряженное тело, пропорционален заряду тела.

20. Закон Кулона в диэлектрике (т. Гаусса для поля в диэлектрике)

21. Свойства проводников

Определение для электростатики:

Проводник - называть любое тело, все точки которого в стационарных условиях и в отсутствии внешних изменяющихся во времени эл-х полей имеют одинаковый потенциал.

*если внешнее поле давно включили и туда проводник внесли давно, всё опять стало стационарно, тоогда наличие внешнего поля никак не влияет на определение.

т.к. = , а поле - градиент потенциала и производная от константы = 0, то из определения проводника: поля внутри проводника нет.

Следовательно напряжённость электростатического поля внутри проводника равна нулю -

Электростатическая экранировка.

На этом основании из теоремы Гаусса: (вычисляем заряд внутри проводника)

(где -произвольная замкнутая поверхность внутри проводника, охватывающая объём V, - поверхность проводника)

Внутри проводника ЗАРЯДОВ НЕТ -» распределяются только по ПОВЕРХНОСТИ ПРОВОДНИКА

Если внести проводник во внешнее электростатическое поле, то заряды на поверхности перераспределятся таким образом, чтобы поверхность (и весь объём) проводника осталась

эквипотенциальной.

Получается всегда ( и в поле, и вне)

(небольшая разница в переносе возникает из-за скорости света, именно поэтому любое внешнее поле немного проникает в проводник)

22 . Метод изображений (для бесконечной проводящей плоскости и сферы)

Метод изображений — частный случай применения функции Грина Задача метода — найти поле в любой точке пространства, где точечный заряд расположен над бесконечно проводящей плоскости.

Для бесконечно проводящей плоскости:

Плоскость проводящая, т.к. по задаче Дирихле потенциал поля одинаков в любой точке этой поверхности плоскость эквипотенциальна.

Весь объем пространства поделен бесконечной плоскостью на две части: объем при Z>0 и объем при Z<0.

Функция Грина для задачи Дирихле(для объема пространства при Z>0): Решение этой теоремы справедливо только для области, где находится реальный физический заряд.

q – реальный заряд (заряды находятся на одинаковом расстояние от делящей плоскости); -q – зеркальный заряд с противоположным знаком;

Электростатическое поле в полупространстве Z > 0,можно интерпретировать,

как суперпозицию двух полей — поля, создаваемого исходной системой зарядов, и поля, создаваемого зарядом-изображением.

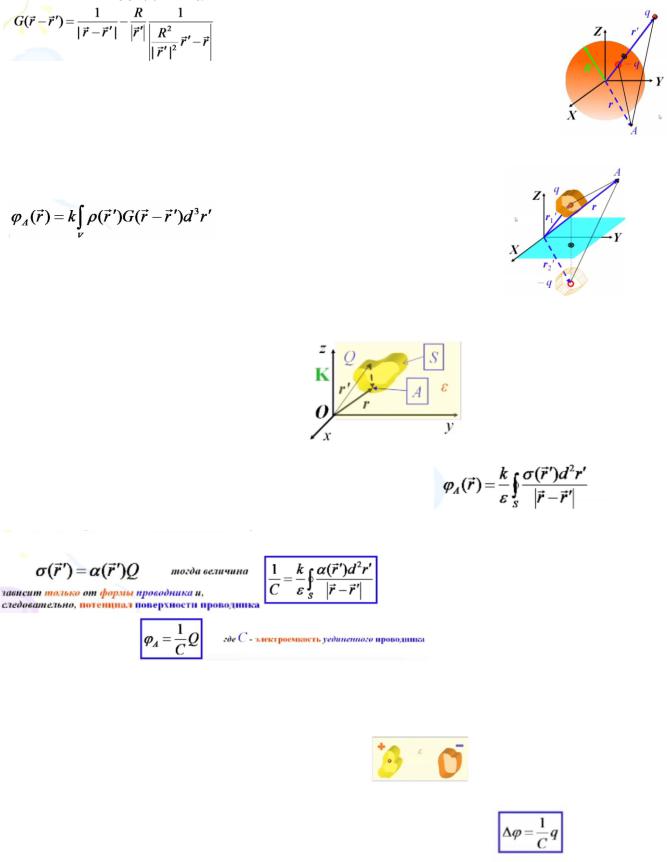
Для сферы:

Для внешней части сферы при|r|>R функция Грина для задачи Дирихле принимает вид:

Для внутренней части сферы при|r|<R функция Грина для задачи Дирихле принимает такой же вид, но взаимно меняются местами вектора r и r’

Второй член в формуле - вклад индуцированного заряда, симметричного данному относительно поверхности сферы

Функция Грина позволяет найти решение как для точечных зарядов, так и для произвольного распределения:

23. Электроёмкость уединённого проводника.

Рассмотрим заряженный проводник (очевидно - плотность распределения заряда по поверхности проводника неравномерна).

Пусть проводник находится в однородной изотропной среде с проницаемостью Ɛ -» потенциал поля в произвольной точке А поверхности проводника:

Поверхность проводника эквипотенциальна -» выражение для потенциала поверхности не должно зависеть от радиус-вектора r -» введём функцию α(r) такую, что

Вопрос 24. Конденсатор – сферический конденсатор.

Рассмотрим два электрически нейтральных проводника, находящихся внутри однородной изотропной среды с диэлектрической проницаемостью .

Перенесем заряд +q с одного проводника на другой.

Взаимная емкость С проводников - способность системы нейтральных проводников изменять свой потенциал в результате переноса заряда с одного проводника на другой.

Конденсатор – любая система двух проводников.

Если проводники нейтральны -» конденсатор не заряжен.

Зарядка конденсатора – процесс переноса заряда с одного проводника на другой.

1. Сферический конденсатор.

Рассмотрим нейтральный проводник сферической формы – чтобы зарядить такой конденсатор, нужно перенести заряд с его поверхности на бесконечность.

Следовательно, сферический конденсатор имеет емкость уединенного проводника и электроемкость сферического конденсатора пропорциональна его радиусу.

Докажем это:

25. Конденсатор - плоский конденсатор.

Рассмотрим систему их двух нейтральных проводящих бесконечны плоскостей, находящихся на расстоянии d. Зарядка такого конденсатора: перенесем заряд (+q) с одной плоскости на другую.

Выносной слайд:

В результате зарядки на плоскостях появится поверхностная плотность заряда (одинаковая по величине). Каждая плоскость создаст свое электростатическое поле: E- и E+. Поле ВНЕ конденсатора компенсируется.

Напряженность поля ВНУТРИ-складывается, а если внутри находится диэлекрик, то:

Зная напряженность, найдем разность потенциалов между пластинами:

По определению взаимной емкости:

Из двух последних (в рамочках) формул, следует:

Вопрос 26. Конденсатор-соединение конденсаторов.

Конденсатор являются одними из основных элементов электрических цепей – как и все элементы их можно соединять параллельно и последовательно.

, при этом Cобщ. = ∑Ci, ,при этом 1/Собщ. = ∑1/Ci

, где n – это общее число соединенных конденсаторов; i – номер конденсатора.

Параллельным соединением любых элементов эл. цепи называют такое соединение элементов, при котором разность потенциалов на всех этих элементов одинаково.

27. Энергия заряженного проводника

Элементарная работа, совершаемая электростатическим полем на элементарном перемещении заряда q равна = ̅ ̅ = ̅̅ = − ̅ ( ̅) = − ( ̅)

Индекс Е означает элект-стат. поле

Неравномерное электростатическое поле с эквипотенциальными поверхностями, которые в каждой точке перпендикулярны линиям поля.

Работа против сил поля А = −АЕ

Работа, которую нужно совершить, чтобы зарядить уединенный проводник до потенциала 0

Для произвольного количества проводников = 12 ∑ =1 0

Работа, проведенная над любым телом – его потенциальная энергия:

- электростатическая энергия заряженного проводника,

где − поверхностная плостность заряда на проводнике

28.Энергия электростатического поля

Система заряженных проводников создает поле с энергией равной сумме потенц. энергий этого поля, либо работе, которую мы совершили(это он словами говорил).

Электростатическая энергия заряженного проводника-это энергия зарядов, перенесенных на проводникследовательно эта энергия численно равна энергии электростатического поля перенесенных зарядов(это определение из презентации).

В отличие от проводников поле находится в любой точке пространства, поэтому переходим к интегралу по объему, а не по поверхности, как в случае с проводниками.

↑↑↑

Выразим из теоремы Гаусса плотность и подставим в интеграл

↑↑↑

Учтем соотношение с наблой, выразим из него скалярное произведение фи на дивергенцию D- 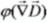, подставим полученную разность в интеграл, а все константы вынесем за знак интеграла.

Получим:

Второй интеграл перепишим в поверхностный и он уйдет в ноль.

Таким образом получим формулу С7:

Мы выразили энергию поля через характеристики поля заряженных проводников.

Для вычисления э/с поля неважно чем оно создано.

Для удобства вводят величину С8, в любой элементарной окрестности поля энергия поля будет такая: