Вопросы к коллоквиуму 3

1. Закон Кулона, Закон сохранения заряда, Принцип суперпозиции О –Закон Кулона. Формула

З акон Кулона – закон, описывающий электростатическое взаимодействие двух точечных покоящихся зарядов. Один заряд действует на другой с силой

Закон сохранения заряда – закон, описывающий важнейшие свойства электрических зарядов: - электрический заряд q является неизменной и аддитивной характеристикой вещества

П ринцип суперпозиции – силы электростатического взаимодействия точечных зарядов складываются по правилу параллелограмма. Для произвольного количества покоящихся(важно только для Кулоновских сил) точечных зарядов:

2. Электростатическое поле (напряженность электростатического поля, поле точечного покоящегося электрического заряда, потенциальность поля)

Электростатическое поле – силовое поле, которое по з. Кулона создает в пространстве вокруг себя любой точечный покоящийся заряд.

Н апряженность электрост. поля – вектор, численно равный кулоновской силе, действующей со стороны заряда q1 на единичный положительный пробный(который не искажает поле в котором находится) заряд qi, помещенный в данную точку.

Э лектростатическое поле потенциально:

3. Основная задача электростатики (для точечных зарядов в вакууме, для произвольного объемного, поверхностного и линейного распределения зарядов) О – (для точечных зарядов в вакууме, для произвольного объемного распределения зарядов в вакууме и диэлектрике)

О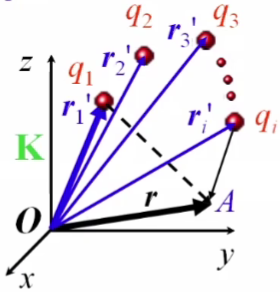 сновная задача электростатики – поиск электростатического поля (напряженность и потенциал) по заданному распределению зарядов.

Д ля системы точечных зарядов в вакууме по принципу суперпозиции:

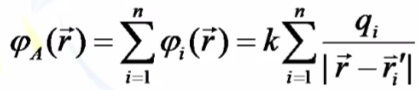
Д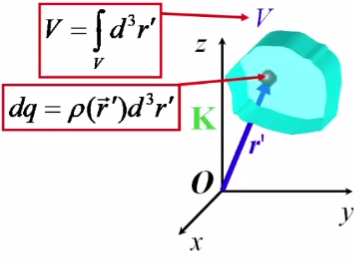 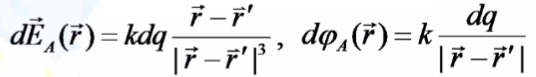ля зарядов с непрерывным распределением в объёме:

Д 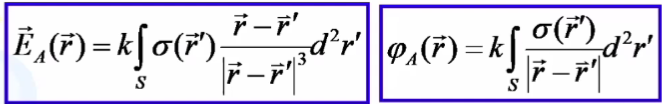ля зарядов с непрерывным распределением по поверхности:

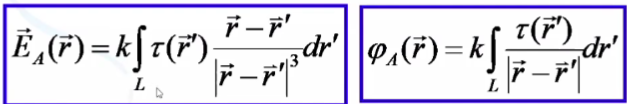
Для линейного распределения с заданной плотностью зарядов :

4. О. Дифференциальные операторы (оператора V (набла), дивергенция функции divF, ротор функции rotF)

О ператор набла формальный вектор, компоненты которого - некоторые объекты, желающие взять частную производную от функции.

Г радиент функции - с действие оператора набла на скалярную функцию

Д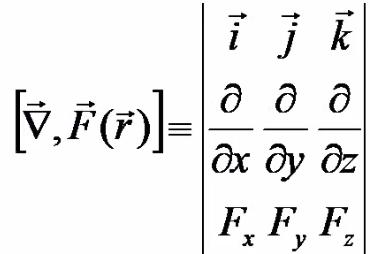 ивергенция функции - - скалярное произведение оператора набла на векторную функцию.

Ротор функции - - векторное произведение оператора набла на векторную функцию

5 . О. Безвихревой характер электростатического поля

В ихревое поле – векторное поле F, ротор которого не равен 0 (нет источников, силовые линии замкнуты на себя)

Э лектростатическое поле - безвихревое – ротор напряженности равен 0

Силовые линии никогда не замыкаются сами на себя, начинаются или заканчиваются на заряде.

6 . Поток вектора напряженности Интегральная сумма скалярных произведений векторного поля E на вектор нормали dS

7. Теорема Гаусса (в том числе - для точечного заряда) О – (вакуум и диэлектрик, интегральная и дифференциальная формы)

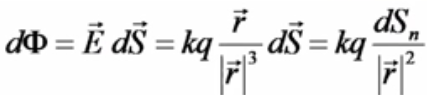
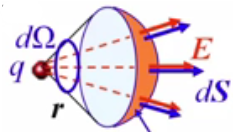Для точечного заряда:

Т.к.

Элементарный объемный (телесный) угол – Тогда Т. Гаусса для точечного заряда:

Элементарный поток dФ вектора напряженности электростатического поля Е точечного заряда q в заданный телесный угол dΩ зависит только от величины заряда q

Т . Гаусса для произвольно заряженного тела тела – поток вектора напряженности электростатического поля через замкнутую поверхность, охватывающую произвольное заряженное тело, пропорционален заряду тела.

Д ля любого элементарного заряда внутри тела , , причем

Окружим тело замкнутой поверхностью, тогда

И нтегрируя по всему объему тела получим: Теорема гаусса –

8 . Применение теоремы Гаусса для расчета полей - поле бесконечной, прямой, равномерно заряженной нити Линейная плотность заряда на нити постоянна Эквипотенциальная поверхность для нити – коаксиальная цилиндрическая поверхность, с заглушками на бесконечности. Для любой точки боковой поверхности цилиндра вектор напряженности Е параллелен вектору нормали к боковой поверхности dSб

Т огда т. Гаусса для нити:

9. Применение теоремы Гаусса для расчета полей - поле бесконечной, равномерно заряженной плоскости

П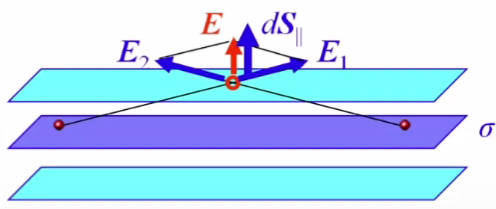 оверхностная плотность заряда на плоскости постоянна Эквипотенциальная поверхность для плоскости – поверхность параллелепипеда Любая бесконечная плоскость – множество бесконечных прямых -» для любой точки поверхностей параллелепипеда, параллельных заряженной плоскости, вектор напряженности Е параллелен вектору нормали к поверхности dS

Т огда т. Гаусса для плоскости:

Напряженность поля над и под плоскостью одинаковы

10. Т. Гаусса для расчета полей - поле сферической, равномерно заряженной поверхности

П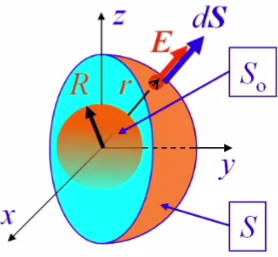 оверхностная плотность заряда на сфере постоянна Эквипотенциальная поверхность для сферической плоскости – сфера Для любой т. поверхности сферы S вектор напряженности Е параллелен вектору нормали к поверхности dS

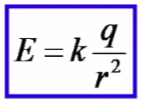Т огда т. Гаусса для сферической равномерно заряженной поверхности:

1 1. Теорема Гаусса в дифференциальной форме (вакуум)

По теореме Остроградского:

Т . Гаусса в диф. форме:

Дивергенция в-ра напряженности электрост. Поля в любой т. пространства пропорциональна плотности заряда в этой точке

1 2. Уравнение Пуассона (вакуум)

Э лектрост-е поле всегда потенциально -»

Тогда из т. Гаусса - Уравнение Пуассона

13. Плотность заряда для точечного заряда (δ – функция Дирака)

δ – функция: В т., где заряда нет – плотность заряда = 0, в т., где заряд есть – плотность равна бесконечности.

Важнейшее св-во δ – функции: Полезный св-ва:

В еличина точечного заряда через плотность заряда и δ – функцию Тогда для точечного заряда

1 4. Поле диполя

Д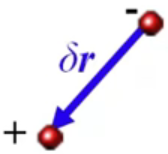 иполе – система сост. из 2х точечных зарядов разных знаков, наход-ся на небольшом расстоянии - плечо диполя, - элем-й дипольный момент

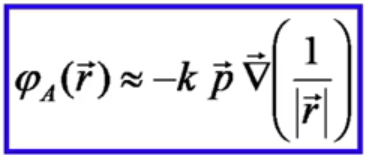
Для неэлементарного диполя:

15. Диэлектрики и вектор поляризации

Диэлектрик – любое в-во, не имеющее собственных свободных носителей тока.

Полярные(гидрофильные) – вода – прямо в пространстве разделены заряды разного знака, имеют собственный дипольный момент Неполярные(гидрофобные) – кислород, парафин – заряды не разделены и диполь не образуют.

Во внешнем силовом поле диэлектрик поляризуется. - в полярном дипольные молекулы выстраиваются вдоль силовых линий поля - в неполярном молекулы поляризуются – вытягиваются вдоль силовых линий, образуя диполи В результате на поверхности диэлектрика появляется эл. заряд.

В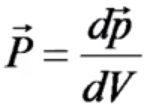 ектор поляризации – в-р, характеризующий дипольный момент диэлектрика в каждой точке внутри диэлектрика.

Л4.16. Основная задача электростатики для поля в диэлектрике (истинные и связанные заряды)

П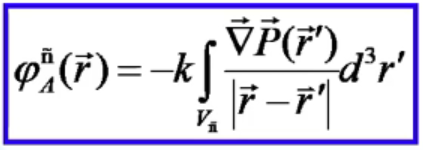 оле, создаваемое всем объемом диэлектрика, описывает потенциал электростатического поля связанных зарядов Истинные и связанные заряды - возникающие за счет поляризации диэлектрика, т.е. наведенные в диэлектрике внешним полем – не могут свободно двигаться

Плотность связанных зарядов -

Р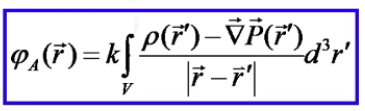 езультирующее электростатическое поле истинных и связанных зарядов:

1 7. Уравнение Пуассона для поля в диэлектрике

1 8. Теорема Гаусса для поля в диэлектрике (+вектор электрического смещения)

Вектор эл-го смещения (в-р индукции)

Т . Гаусса для поля в диэлектрике: Дивергенция вектора электрического смещения электростатического поля в любой т. пространства пропорциональна плотности истинных зарядов в этой точке

19. Т. Гаусса для поля в диэлектрике (интегральная форма)

П оток вектора индукции электростатического поля через замкнутую поверхность, охватывающую произвольно заряженное тело, пропорционален заряду тела.

2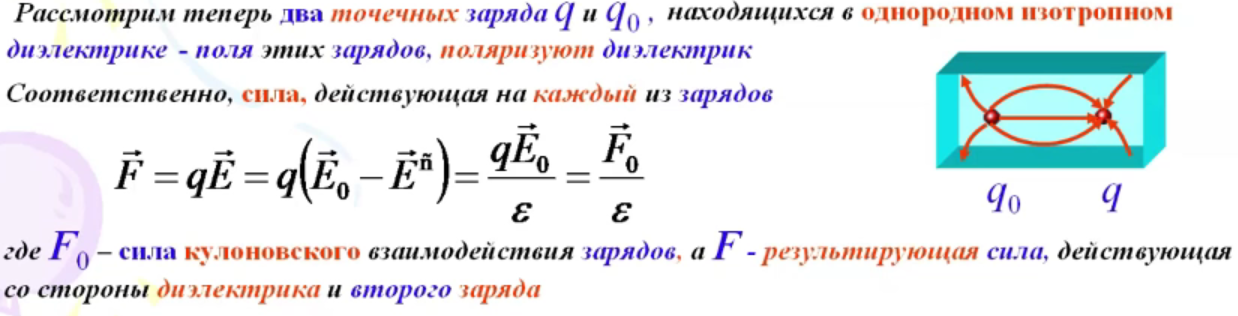 0. Закон Кулона в диэлектрике (т. Гаусса для поля в диэлектрике)