
методичка 2003 часть 2 (новый вариант)
.pdf
Если подобный анализ выполнить для бόльшего числа разделительных конденсаторов (например, N), то вид формулы (13.4) не изменится – добавятся только дополнительные сомножители в ее знаменателе:
|
|
|
|
|
K0 |
|
|
|
, |
(13.5) |
|
KΣ |
1 |
|
|
1 |
|
|
1 |
|
|||
|
(1 |
)(1 |
|
) (1 |
|
) |
|
|
|||
|
|
|
|
|
|
||||||
j н1 |
j н2 |
j нn |
|
|
|||||||
где нп - постоянная времени низких частот n - го разделительного кон-
денсатора.
Поэтому в общем случае АЧХ и ФЧХ многокаскадного усилителя:
|
|
|
|
|
|
|
|
|
|
|
K0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
KΣ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, (13.6) |
|
|
1 |
1 |
|
|
1 |
1 |
|
|
|
1 |
1 |
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
( |
н1 |
)2 |
( |
н2 |
)2 |
( |
нn |
)2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Σ arctg |
1 |
arctg |
|
1 |
|
arctg |
1 |
. |
|
|
|||
|
|
|
|
|
|
|
|
||||||
н1 |
н2 |
нп |
|
|
|||||||||
|
|
|
|
|
|
|
|
||||||
Если в формуле (13.6) перемножить выражения под знаком |
|
и учесть, |
|||||||||||
|
|||||||||||||
что вблизи f н выполняются неравенства |
|
|
|
|
|
|
|||||||
|
|
1 |
|
|
|
1 |
1, |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
н2 |
|
|
|
|
|||
|
|
н1 |
|
|
|
|
|
||||||
то приближенная формула для АЧХ усилителя с n – разделительными конденсаторами будет иметь вид:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K0 |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
KΣ |
|
|
|
|
|
|
|
, |
(13.7) |
||||
|
|
|
|
|
|
|
|
|
1 |
1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 нр2 |
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
где |
|
1 |
|
|
1 |
|
|
1 |
|
|
|
1 |
|
|
- эквивалентная постоянная времени, |
|||||||
2 |
2 |
2 |
2 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
нр |
|
|
н1 |
|
|
н2 |
|
|
|
|
нп |
|
|
|
|
|||||
учитывающая влияние на АЧХ n - разделительных конденсаторов.
Учет совместного влияния разделительных и блокирующих конден-
саторов на АЧХ усилителя. Анализ каскада с блокирующим конденсатором (рис.10.1) показывает, что вблизи f н его АЧХ имеет такой же вид, что и АЧХ
усилителя с разделительными конденсаторами. Поэтому учет влияния C рп и
Сэm приведет к добавлению в формулу (13.5) еще n-сомножителей, обусловленных m - блокирующими конденсаторами:
71

|
|
|
|
|
|
|
|
|
|
|
K0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
KΣ |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
|
|
1 |
|
. (13.8) |
||
|
|
|
1 |
|
|
1 |
|
1 |
|
|
1 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
2 н21 |
2 нп2 |
2 нб2 1 |
2 нб2 m |
|
|
|
||||||||||||
Поэтому суммарная АЧХ в диапазоне низких частот:
|
|
|
|
|
|
|
|
KΣ |
|
|
|
|
|
|
K0 |
, |
|
(13.9) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
1 |
1 |
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 н2Σ |
|
|
|
|
||||||||||
где |
|
1 |
|
|
1 |
|
|
1 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
н2Σ |
нр2 |
нбп2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
1 |
|
|
|
|
1 |
. |
(13.10) |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
2 |
|
|||||
|
|
|
|
|
|
|
|
|
|
нб |
|
|
|
|
нб1 |
|
нбт |
|
|||||||||
Суммарная эквивалентная постоянная времени низких частот нΣ выражается через постоянные времени нi , которые находятся путем определения Rэкв.i , включенного между выходами i – го разделительного (блокирующего) конденсатора при условии, что все остальные конденсаторы закорочены.
1п |
|
С рп |
|
1л |
1п |
1л |
|
С р1 |
|
Rэкв. pп |
|
|
|
Сб1 |
|
|
Rэкв. р1 |
Rвх3 |
|
|
|
Rэкв.б1 |
|
1л |
1п |
Рис.13.4. К определению эквивалентных постоянных времени низких частот
Вх |
1 |
2 С р2 |
Вых |
|
|
A1 |
|
R1 |
С р1 |
3 |
|
|
|
|
|
евх |
R3 |
Сб1 |
|
|
Rн |
72

Рис.13.5. Схема к расчету постоянных времени низких частот усилителя |
||||||
|
|
на микросхеме А1 |
|
|
||
Так для схемы (рис.13.5) |
|
|
|
|
|
|
|
н1 (R1 Rвх1) C р1; |
|
|
|||
|
н2 |
(Rвых2 Rн ) С р2 ; |
|
|||
|
н2 R3 || Rвых.3Cб1, |
|
|
|||
где |
Rвых2 , Rвых3 – выходные сопротивления усилителя А1 относи |
|||||
|
тельно выводов 2 и 3, |
|
|
|||
|
Rвх1 - входное сопротивление усилителя А1. |
|
||||
Нормированные АЧХ усилителя в диапазоне низких частот. В соот- |
||||||
ветствии с определением коэффициента частотных искажений М, из получен- |
||||||
ной выше формулы для АЧХ многокаскадного усилителя 13.9 можно найти: |
||||||
|
|
|
|
1 |
|
|
|
M |
KΣ |
|
. |
(13.11) |
|
|
K0 |
1 |
||||
|
|
1 |
|
|
||
|
|
|
2 2 |
|
|
|
|
|
|
|
н |
|
|
|
M |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
f |
|
|
f н |
|
|
|
|
|
Рис.13.6. Нормированные АЧХ усилителя |
|
||||
Таким образом, нижняя граничная частота н 2 fн усилителя может быть найдена из уравнения
1 |
|
|
|
|
|
1 |
|
|
. |
(13.12) |
|
|
|
|
|
|
|
|
|
|
|||
2 |
|
|
1 |
|
|||||||
1 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|||||
|
|
н2 н2Σ |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
После преобразований (13.12), находим
73

|
|
1 |
. |
(13.13) |
|
||||
|
нΣ |
|
||
При решении задачи анализа конкретного усилителя определяется коэф- |
||||
фициент М на заданной частоте ω при известной нΣ . |
|
|||
В тех случаях, когда решается задача синтеза, т.е. |
при заданных f н и |
|||
М= 12 0,707 , становится известной только сумма неизвестных частных по-
стоянных времени, необходимо рационально «распределить» эту сумму между n-частными постоянными времени. Например, известно, что
1 |
|
|
1 |
|
1 |
|
|
1 |
2 3600c 1. |
||
|
|
|
|
|
|
||||||
н2Σ |
|
н21 |
н22 |
|
н23 |
||||||
Каждую частотную постоянную времени, входящую в последнюю формулу, можно определить двумя способами:
а) путем равномерного распределения вносимых частотных искажений между всеми разделительными и блокирующими конденсаторами:
|
1 |
|
1 |
|
1 |
; |
|
|
|
|
|
|
|||
н1 |
н2 |
н3 |
|||||
б) путем неравномерного распределения вносимых частотных искажений |
|||||||
между разделительными и блокирующими конденсаторами: |
|||||||
|
1 |
|
|
1 |
|
|
1 |
. |
|
|
н2 |
|
|||||
н1 |
|
н3 |
||||||
В первом случае при существенных различиях между Rэкв1 и Rэкв2 емкости конденсаторов С р1 и С р2 будут сильно отличаться друг от друга.
Это не технологично, так как габариты конденсаторов будут неодинаковы. Второй способ выбора постоянных времени часто дает более оптималь-
ные (в смысле габаритных показателей) расчеты. Однако он требует предварительной оценки численных значений Rэкв.i .
74

14 УСИЛИТЕЛЬНЫЕ КАСКАДЫ С RCСВЯЗЬЮ В ДИАПАЗОНЕ ВЫСОКИХ ЧАСТОТ
На высоких частотах вид АЧХ и ФЧХ каскада определяется высокочастотными свойствами применяемого активного элемента (транзистора) и схемой его включения, а также влиянием инерционностей в его входной и выход-
ной цепях (как правило – входной Свх и выходной Сн емкостями)
Вх |
Rc |
|
|
|
Вых |
|
|
uвх |
активный |
|
uн |
|
|
элемент |
Rн |
||
|
Rвх |
|
|
Сн |
|
ec |
Свх |
|
|
|
|
|
|
|
|
Рис.14.1. Функциональная схема усилителя на высоких частотах
В схеме (рис.14.1) Cвх , Rвх - входная емкость и входное сопротивление активного элемента с учетом монтажа; Rн - эквивалентное сопротивление
нагрузки, учитывающее выходное сопротивление усилительного прибора и входное сопротивление последующей цепи.
|
|
Rc |
активный элемент |
||||||||
Вх |
|
|
Вых |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Е c |
|
R |
н |
С |
н Uн |
Rвх |
U вх |
|
|
||
Свх |
|
|
|
||
|
|
SU вх |
|
|
|
Рис.14.2. Упрощенная эквивалентная схема усилителя (рис.14.1)
Из рассмотрения схемы (рис.14.2) можно найти комплекс входного напряжения:
Uвх Eс Kвх.ц ;
75

|
|
|
|
|
Rвх || |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
j C |
|
|
|
Kвх.ц |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
вх |
|
|
|
|
, |
(14.1) |
||
|
|
Kвх.ц |
|
|
|
1 |
Rс |
1 |
j в.вх |
||||||
|
|
|
|
Rвх || |
|
|
|
|
|||||||
|
|
|
|
j Cвх |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где |
Kвх.ц |
Rвх |
|
|
- коэффициент передачи делителя Rc - Rвх в диа- |
||||||||||
Rвх Rс |
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
пазоне средних частот;
в.вх Cвх (Rс || Rвх ) - постоянная времени высоких частот вход-
ной цепи.
Выходное напряжение:
|
|
1 |
|
|
|
|
|
|
|
SUвх Rн |
, |
(14.2) |
|
Uн SUвх Rн || |
j Cн |
1 j в.н |
||||
|
|
|
|
|
||
где в.н Сн Rн .
Емкость нагрузки, как правило, складывается из следующих составляю-
щих: |
|
Cн Cвых.у.э CM Cвх.п , |
(14.3) |
где Свых. у.э - выходная емкость активного элемента;
См - емкость монтажа;
Cвх.п - входная емкость последующей цепи (нагрузки).
|
|
|
|
|
|
|
|
|
|
|
|
|
В общем случае крутизна S активного элемента (АЭ) (усилительного |
||||||||||||
прибора) является функцией частоты. Будем приближенно считать, что: |
|
|
|
|||||||||
|
|
|
|
|
S0 |
|
|
|
|
|
||
|
S |
1 j в.s |
, |
|
(14.4) |
|||||||
где S0 - крутизна преобразования входного напряжения в выходной ток |
||||||||||||
АЭ в диапазоне средних частот; |
|
|
|
|
||||||||
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 - |
|||
в.s в.s - граничная частота, на которой S уменьшается в |
||||||||||||
раз. |
|
|
|
|
|
|
|
|
|
|
|
|
Для схемы с ОЭ и ОБ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
S0 |
|
Iэ. р |
. |
|
|
(14.5) |
|||||
|
|
T |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Следовательно, комплексный коэффициент усиления для таких схем: |
||||||||||||
|
Uн |
|
|
|
|
Kвх.ц RнS |
|
|
|
|
||
Kе |
|
|
|
(1 j в.вх )(1 j в.н ) |
, |
(14.6) |
||||||
|
Eс |
|
|
|
|
|
|
|
||||
76

|
|
|
|
|
|
|
|
|
|
или с учетом комплексного характера S : |
|
|
|
|
|
||||
|
|
|
|
|
K0 |
|
|
, |
(14.7) |
|
|
Kе |
j в.вх )(1 |
j в.н )(1 j в.s ) |
|||||
|
|
(1 |
|
|
|||||
где K0 Квх.ц RнS0 - коэффициент усиления в диапазоне средних ча- |
|||||||||
|
|
|
стот. |
|
|
|
|
|
|
Поэтому уравнения для АЧХ и ФЧХ: |
|
|
|
|
|
||||
|
|
|
|
|
K0 |
|
|
; |
(14.8) |
|
| Kе | |
|
|
|
|
|
|||
|
|
1 2 в2.вх 1 2 2в.н 1 2 2в.s |
|
||||||
|
arctg в.вх arctg в.н arctg в.s . |
|
|
||||||
K |
|
|
|
|
|
|
|
|
|
20 lg K0 |
* |
*3дБ* |
* |
* |
* |
|
область |
|
|
|
несущественных |
||||||||
|
|
|
|
|
* |
|
|||
|
|
|
|
|
|
частот |
|
||
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
* |
2 f |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
1 |
1 в |
* |
|
|
|
|
|
|
|
1 |
|
|
|
||
|
|
|
|
в.вх |
в.н |
в.*s |
|
|
|
Рис.14.3. Логарифмическая АЧХ каскада в диапазоне высоких частот для |
|||||||||
случая, когда τв.вх> τв.н> τв.s |
|
|||||
|
|
1 |
|
1 |
1 |
|
|
|
|
|
|||
* |
|
в.вх |
|
в.н |
в.s |
2 f |
* |
1 |
2 |
s |
|
||
|
|
|||||
-90 |
|
* |
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
1 |
+ 2 |
+ s |
|
|
|
|
|
|||
-180 |
|
|
|
* |
|
|
|
|
|
* |
|
||
|
|
|
|
|
||
|
|
|
|
|
* |
* |
-270 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.14.4. ФЧХ каскада |
|
|||||
77

Если учесть, что область очень высоких частот нас часто не интересует, то уравнение для АЧХ вблизи в можно упростить путем перемножения сомножителей в знаменателе формулы (14.8):
(14.9)
где в.Σ
(14.10)
Полученные выше соотношения являются универсальными, независящими от типа активного элемента (биполярный или полевой транзистор) и схе-
мы его включения. Расчет с их помощью |
поведения того или иного каскада в |
||
диапазоне высоких частот сводится, прежде всего, к определению в.s и |
S0 на |
||
основе одной из высокочастотных моделей усилительного элемента. |
|
||
Для получения больших значений |
f в |
необходимо иметь как |
можно |
меньшие значения постоянных времени в.вх , |
в.н , в.s . Две первые посто- |
||
янные времени уменьшаются с уменьшением |
Rс (Rвх ) и Rн . Однако при |
||
этом ухудшается и К0 . На это приходится идти в широкополосных усилителях, где К0 одного каскада иногда не превышает 2-5.
Постоянная времени в.s существенно зависит от типа активного элемента и его режима по постоянному току (чем больше статический ток эмиттера транзистора, тем, как правило, меньше в.s ).
78
15МНОГОКОСКАДНЫЕ УСИЛИТЕЛИ С RC-СВЯЗЬЮ В ШИРОКОМ ДИАПАЗОНЕ ЧАСТОТ
Амплитудно-частотная характеристика усилителя, содержащего несколько каскадов, в существенном диапазоне низких частот описывается полученными выше уравнениями
|
|
K0 |
|
|
|
|
|
|
K0 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
||||||||
Ке |
|
1 |
|
; |
Kе |
|
|
|
|
|
|
|
. |
(15.1) |
||
|
|
|
|
|
|
2 |
|
|||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|||||
j н.Σ |
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
2 |
н.Σ |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично, с учетом выводов раздела 14 в существенном диапазоне высоких частот АЧХ того же усилителя аппроксимируется выражением:
|
|
|
|
K0 |
|
, |
|
|
|
K0 |
2 . |
(15.2) |
||
|
Ке |
|
|
Kе |
|
2 |
||||||||
|
|
1 |
|
|
j |
в.Σ |
|
|
|
1 |
в.Σ |
|
||
|
|
|
|
|
|
|
|
|
|
|||||
K у |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
K0 |
|
|
|
|
* |
|
* |
|
* |
* |
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
К0 |
|
|
|
* |
|
|
|
|
|
|
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
* |
|
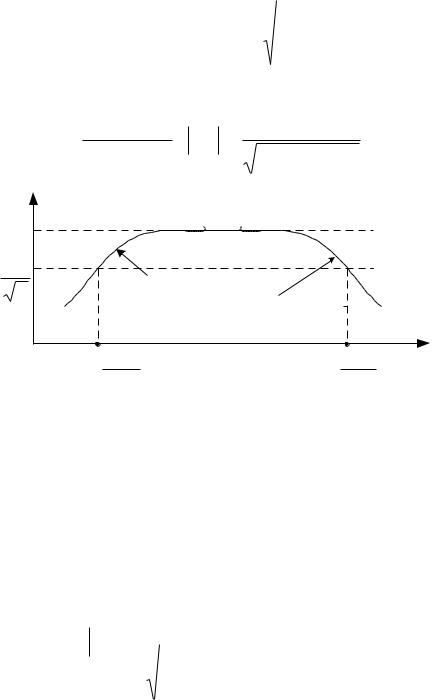
формула (15.1) |
формула (15.2) |
|
* |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
н |
|
1 |
|
|
|
|
|
в |
|
1 |
|
||
|
н.Σ |
|
|
|
|
|
в.Σ |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||
Рис.15.1. АЧХ усилителя в широком диапазоне частот |
|
|||||||||||||
Таким образом, во всем частотном диапазоне от ωн до ωв: |
|
|||||||||||||
|
|
|
K0 |
|
|
|
K0 |
|
|
||
Kе |
1 |
|
|
|
|
1 |
|
. (15.3) |
|||
|
(1 |
|
)(1 |
j в.Σ ) |
1 j( |
|
в.Σ ) |
||||
|
|
|
|
|
|||||||
|
|
н.Σ |
|||||||||
|
|
j н.Σ |
|
|
|
|
|
||||
Так как отношение τв.∑/τн.∑ для широкополосных усилителей значительно меньше единицы, уравнение для АЧХ широкополосного многокаскадного усилителя в широком диапазоне частот будет иметь вид:
|
|
|
|
|
|
K0 |
|
|
|
|
|
|
|
|
|
||||||
Kе |
|
|
|
|
|
|
. |
(15.4) |
||
|
|
1 |
|
в.Σ )2 |
||||||
|
|
|
1 ( |
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||
|
|
|
|
|
н.Σ |
|
|
|
||
79
Следует иметь в виду, что эта формула приближенная. Она плохо работает на частотах меньших ωн и больших ωв. Еще большая погрешность получается при расчете ФЧХ усилителя на основе формулы (15.4).
Сложные многокаскадные усилители удобно анализировать с помощью ЭВМ, например, программы PSpice, Orcad и др.
80
