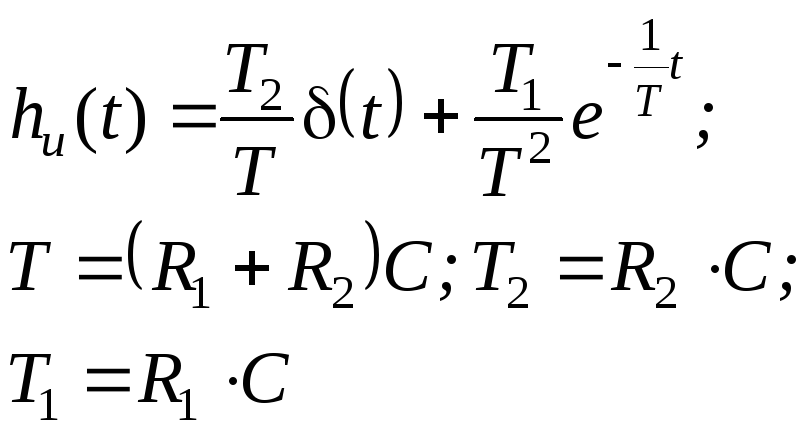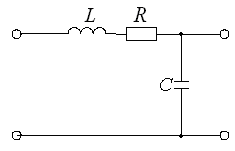
Импульсные характеристики и переходные функции цепей

Схема	Аналитическое выражение
1	2
Продолжение табл. 4.6
1	2
	где –a и –b – корни уравнения
Окончание табл. 4.6
1	2

Студентам заочной формы обучения при выполнении третьего раздела курсовой работы необходимо определить частоты, на которых выполняются условия резонанса токов и резонанса напряжений для короткозамкнутого отрезка кабеля без потерь длиной с первичными параметрами. Найти входное сопротивление кабеля на частотеЗначениявыбрать из таблицы 4.7. Кроме того, определить наименьшую длину разомкнутого отрезка кабеля без потерь с первичными параметрами, входное сопротивление которого на частоте 100 МГц эквивалентно емкости С. Значения параметроввыбрать из таблицы 4.8.

Номер варианта задания соответствует последней цифре шифра зачетной книжки студента.

Таблица4.7

Параметры кабеля

Номер варианта			ℓ, м
0	2,6∙10-4	46,5∙10-9	1,0
1	4,5∙10-4	50,0∙10-9	1,5
2	5,0∙10-4	62,3∙10-9	2,0
3	3,0∙10-4	80,0∙10-9	2,5
4	4,0∙10-4	75,4∙10-9	1,0
5	3,5∙10-4	53,6∙10-9	3,0
6	3,0∙10-4	60,0∙10-9	2,0
7	6,0∙10-4	28,7∙10-9	1,5
8	4,0∙10-4	25,0∙10-9	2,5
9	2,5∙10-4	40,0∙10-9	3,5

Таблица4.8

Параметры нагрузки и однородной двухпроводной линии

Номер варианта
0			100
1			250
2			330
3			180
4			300
5			500
6			220
7			150
8			200
9			430

5 Методические указания к выполнению

КУРСОВОЙ РАБОТЫ

5.1 Классический метод анализа переходных процессов

Классический метод анализа переходных процессов в электрической цепи основан на использовании неоднородных линейных дифференциальных уравнений с постоянными коэффициентами, выражающих законы Кирхгофа [3]:

(5.1)

Решение уравнения (5.1) представляет собой сумму общего решения однородного уравнения:

(5.2)

и частного решения неоднородного уравнения (5.1). Общее решение уравнения (5.2) описывает свободную составляющую переходного процесса , частное решение уравнения (5.1) – принужденную составляющуюТаким образом, переходной процесс складывается из свободной и принужденной составляющих:

Свободная составляющая переходного процесса определяется только свойствами цепи и не зависит от вида входного воздействия. Для ее нахождения записывают и решают характеристическое уравнение для дифференциального уравнения (5.2):

(5.3)

Если – корни характеристического уравнения (5.3), причем, среди них нет равных, то решение уравнения (5.2) запишется в виде:

(5.4)

где А₁,…,А_n – постоянные интегрирования, определяемые начальными условиями.

Из выражения (5.4) видно, что свободная составляющая состоит из n линейно независимых слагаемых.

Если k корней характеристического уравнения равны между собой:

то решение однородного уравнения запишется в виде:

(5.5)

Решение (5.5) справедливо и в случае k=n.

Если одна или несколько пар корней уравнения (5.3) является комплексно сопряженными и не равны друг другу:

то решение будет содержать слагаемые вида:

где – собственные частоты и собственные затухания составляющих, определяемые параметрами цепи.

Общее решение x_св(t) будет иметь в этом случае следующий вид:

(5.6)

Величины А_k, A_k+2 и , находятся, исходя из начальных условий.

Если какая-либо пара комплексно сопряженных корней имеет кратность k (k пар комплексно сопряженных корней равны между собой), то соответствующие k пар членов в формуле (5.4) заменяются слагаемыми

,

где постоянные интегрирования с₁, с₂,…,с_k и b₁, b₂,…,b_k определяются из начальных условий.

Принужденная составляющая определяется как отклик цепи на входное воздействие при, когда свободная составляющаяпрактически затухает. Вид принужденной составляющейопределяется входным воздействиемВ том частном случае, когдаесть величина постоянная, равная, частное решение находится из равенства:

(5.7)

Для определения частного решения уравнения (5.1) при других видах входного воздействия необходимо воспользоваться известными методами решения неоднородных линейных дифференциальных уравнений с постоянными коэффициентами [6].

Постоянные интегрирования определяются после нахождения частного решения уравнения (5.1) и общего решения уравнения (5.2) по известным начальным условиям. В качестве независимых начальных условий используются величины токов индуктивностей и напряжений на емкостях в момент времени t=0, т.е. В качестве зависимых начальных условий используются значения производных токов и напряжений в момент времениt=0.