Раздел 4 Элементы теории относительности.
Постулаты СТО. Зависимость массы тел от скорости. Преобразование координат и времени. Новые результаты СТО. Законы сохранения .
Как и многие научные теории - теория относительности (ТО)
строится на постулатах.
1. Скорость света в вакууме не зависит от
скорости движения источника или приемника
т.е. скорость света С=const.
Эксперимент с электронами показал, что
максимальная скорость их движения не превышает «с», хотя энергия их растёт пропорционально работе источника: Объяснение кроется в зависимости массы от скорости.
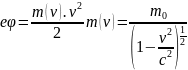2.
Все законы физики выполняются во всех
инерциальных системах, то есть все
наблюдатели S равноправны.
В t = 0 S и S’ находятся в одной точке, потом происходит движение.
Разместим
лампочку в 0. Фронт волны в S:
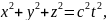Фронт
сфера
В
S’
такой фронт волны – сфера:
При переходе из S в S’: равноправие наблюдателей удовлетворяется, если и координаты и время подвергнуть преобразованиям: y’=y; z’=z;
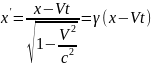(1),
где
(2)
При переходе из S’ в S: y=y’; z=z’;
(3)
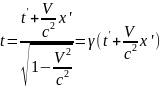(4).
Если
,
то x,
t
– мнимые, следовательно
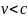
Если найти
с учётом (1) и (2), то получим
.
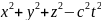Таким образом удовлетворяем второму
постулату. Эта величина называется в
СТО-интервалом. Она = Const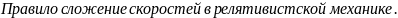
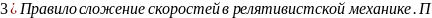Дифференцируем (3) и(4):
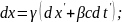dt=
).
Здесь
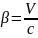Найдём
скорость:
=
.
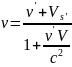4. Сокращение длины.
Пусть
в системе S
имеется жесткая линейка L.Наблюдатель
измеряет её, когда концы совпадают
одновременно с точками
.
У неподвижной линейки это совпадения
концов не зависят от времени, следовательно
есть длина покоя линейки. Наблюдатель
системы
,
движущийся со скоростью V, относительно
S,
измеряет длину (для него подвижной) той
же линейки, когда её концы одновременно
(
)
по его часам , совпадают с точками
.
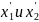Длина линейки тогда
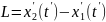
Сравним сделанные измерения:
.
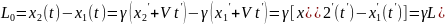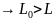-длина
движущейся линейки оказывается короче.
Это лоренцево сокращение длины.
Если повторить опыт, поместив линейку в системе (где она будет неподвижна), то вновь движущаяся линейка , измеренная наблюдателем S, окажется короче.
5).Замедление
времени.
В системе S.в одном месте X = const;
событие длится от
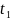до
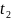.Интервал cобытия
в неподвижной системе
.За
этим событием наблюдает S’по
своим часам
,
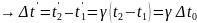то есть
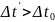Если наблюдатель
’
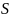наблюдает событие в точке X’
= const,
длящееся от
асам
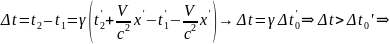интервал
времени в системе движущейся, больше,
чем в покое.
6).События, происходящие в одной точке в системе S в разные промежутки времени -в S' различны и во времени и в пространстве. Собственное время определяется по часам движущейся точки - есть инвариант, относительно преобразований Лоренца.
7)
Законы Ньютона. Примем выполнение
первого и третьего законов априори.
Второй - применим к точке, движущейся с
релятивистской скоростью (общий
случай)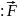
(r,v.t)=
[
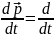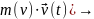
(r,v.t)
=
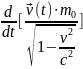
Можно записать дифференциальные уравнения движения в проекциях на оси естественной системы координат.
;
.
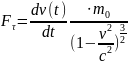8)
Закон
сохранения массы.
разложим в ряд (бином Ньютона). Для
первых двух членов ряда:
=
;
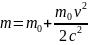В замкнутой системе сохраняется полная
масса тел,
Этот закон позволяет превращать частицу с меньшей массой покоя в частицу с большей массой.
9).
Закон
сохранения релятивистской
энергии:
