4. Математическая модель. Классификация механического движения по ускорению.

Отличить характер одного движения от другого можно по многим параметрам: по виду траектории, характеру изменения скорости и т д. Наиболее общим (в информативном смысле) считается классификация по ускорению. Ускорение непосредственно связано с причиной изменения состояния движения –силой. Пусть вектор скорости меняется с течением времени и по величине, и по направлению. Любой вектор (см.Приложение1) равен своей длине, умноженной на единичный вектор того же направления: 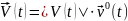. Тогда по определению ускорения:

. Здесь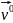 - единичный вектор направления ). – тангенциальное ускорение, характеризует изменение вектора скорости 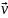только по величине.

– нормальное ускорение, характеризует изменение вектора скорости только по направлению.

Случай 1. , вектор скорости не изменяется ни по величине , ни по направлению ( , это – равномерное, прямолинейное движение. Найдём параметры и закон движения. Начальные условия: t=0 R(0) =

Закон движения: в векторной системе отсчёта

Любое векторное уравнение может быто записано в скалярной форме. Для этого выберем, например, декартову системе координат и поместим её начало в точке отсчёта. Тогда проекции радиус-вектора на оси декартовой системы будет равна соответствующем координатам движущейся точки: или .- Одно векторное уравнение движения эквивалентно трём скалярным в декартовой системе координат.

Случай 2. равнопеременное, прямолинейное движение ( );

(равноускоренное или равнозамедленное )

Так как вектор скорости не меняется по направлению ( ), то пусть движение происходит по направлению оси OX. При этом важно, чтобы вектор начальной скорости и ускорение были коллинеарные. Найдём параметры и закон движения в декартовой системе координат.

; - уравнение движения В векторной системе отсчёта: 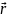= 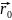+ t + ;

Случай 3. Это означает, что модуль вектора скорости не меняется, в то время как за любые равные промежутки времени его направление меняется на равные углы. Это криволинейное равномерное движение. Это- равномерное движение по окружности Уравнение плоского криволинейного движение проще рассматривать в полярной системе координат.

Цилиндрическая, полярная система отсчета. Тело (точка) отсчета называется полюс. Чтобы задать положение материальной точки относительно полюса нужны 3 числа: здесь В цилиндрической системе отсчета удобно описывать движение тела (материальной точки) по окружности В этом случае если точка отсчёта взята в центре окружности, расположенной в плоскости к оси Z . Тогда положение точки относительно полюса зависит только от 𝜑 – определяет уравнение движение точки по окружности. Введём параметры движения, называемые угловыми, в полярной системе: угловая скорость; = –угловое ускорение. . Связь линейных и угловых координат: dS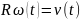=R , , R = , 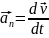Найдём закон движения:

=

.

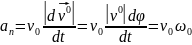Закон движения:

Случай 4 Движение равнопеременное движение по криволинейной траектории 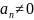. Полагая R=Const (связь с телом отсчёта) -траектория окружность.

Угловое ускорение в силу Найдём параметры и закон движения в угловых переменных. Угловая скорость.

закон движения.

Следует отметить идентичность законов поступательного и вращательного движений в «своих» системах отсчёта.

Случай 5. Движение, при котором координаты точки повторяются через равные промежутки времени (периоды), называется колебательным движением. Простейшими периодическими функциями являются гармонические функции времени - синус или косинус. При этом как первая, так и вторая их производные будут также гармоническими функциями. Поэтому легко «угадать» вид ускорения при гармонических колебаниях материальной точки:

Для данного случая можно решить обратную задачу кинематики: по заданному закону движения найти параметры.

Пусть система совершает движение вдоль оси OX по закону: ,

где - амплитуда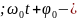 фаза колебаний.

Тогда

: Ускорение материальной точки, совершающей гармоническое колебательное движение, пропорционально смещению от положения равновесия и направлено в сторону положения равновесия.

Постоянные интегрирования, начальная фаза 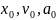, находятся из начальных условий при решении динамических дифференциальных уравнений колебаний. Циклическая частота (число полных колебаний за 2 секунд) зависит от колебательных свойств системы.

Случай 6. Волновое движение. Процесс распространения

колебаний в пространстве с течением времени –

волновой процесс или волна. Механическая Система

представляет собой некоторую среду, состоящую из

множества точек, связанных упругими силами. Рассмотрим Рис.1.

одномерную модель среды.

Это простейшая модель волнового процесса – плоская волна.

В плоской волне каждая материальная точка среды имеет координаты x,y. Пусть точка с координатой x=0 совершает колебание вдоль оси OY по закону: ,

Полагаем далее, что затухания нет, следовательно, амплитуда колебаний для всех точек по оси OX одинакова: . Смещение точек по оси OX не происходит (поперечная волна) Смещение первой точки нарушает равновесие второй точки и т.д.

Вдоль оси OX начнётся распространяться процесс колебаний c некоторой скоростью Заметим, что все частицы начинают движение от положения равновесия так же, как и первая, но с запаздыванием по времени на . Тогда время начала колебаний произвольной точки вдоль оси OX будет функцией координаты. Можно сформулировать словесное описание такого процесса как: некая точка среды начинает своё колебательное движение как начинала его первая 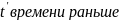. Соответственно математическая запись закона распространения колебаний y

Итак, закон волнового движения, уравнение волны:

Важнейшим параметром волнового процесса является длина волны это расстояние, на которое распространится волна за время, равное периоду колебания Т, то есть . Поскольку период связан с линейной частотой (числом колебаний за 1 секунду) ,то .

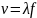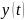
Заметим, что когда через время t=T первая точка x=0 начнёт своё второе колебание, другая точка с координатой x= начнёт своё, точно такое же движение, первый раз. Через некоторое время на оси уже будет множество точек, которые имеют одинаковые значения Говорят, что они колеблются в одинаковой фазе. Не трудно понять, что любые две точки волны, отстоящие друг от друга на расстояние , будут обладать таким свойством. Тогда: кратчайшее расстояние между точками, колеблющимися в одинаковой фазе – длина волны.

Волновое число можно связать с длинной волны:

Итак, кинематические уравнения материальной точки по видам движения:

1. Уравнение поступательного движения: ;

2. Уравнение вращательного движения: ; + ;

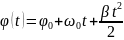3. Уравнение колебательного движения: ; v(t) =

. Здесь = ; ; - зависит от колебательных (упругих) свойств системы.

4. Уравнение волнового движения: ; скорость волны зависит от упругих свойств среды.