Скорость звука как волны.

Звуковые волны имеют частоты в пределах 16-20 000 Гц. Источником звука может быть всякое тело, колеблющееся в упругой среде со звуковой частотой.

В истории развития физических знаний известны различные формулы, по которым определялась в разные времена скорость звука :

1) формула Ньютона (6) – выводится в предположении, что процесс распространения звука в газе можно считать изотермическим; здесь- давление газа,- плотность газа; ее результаты расходятся с экспериментом.

2) формула Лапласа (7) или, где- термодинамический коэффициент, равный отношению удельных теплоемкостей газа; формула выводится на основе утверждения, что процесс распространение акустических волн являетсяадиабатическим; формула (7) соответствует опытным данным.

Т.к. плотность газа зависит от температуры: , где- плотность газа при 0⁰С, t – температура в ⁰С, - коэффициент расширения газа (), следовательно,

(8).

При 0⁰С скорость звука в воздухе =331,5 м/с.

Что же представляет собой скорость звука? Скорость звука есть скорость распространения упругих колебаний в среде – твердой, жидкой или газообразной.

Пусть резким движением поршня в трубе вы создали уплотненный слой воздуха. А потом вернули поршень в первоначальное положение. Подобно сжатой пружине, слой воздуха начнет расширяться в обе стороны, заполняя образовавшееся разрежение слева и вызывая сгущение справа. Таким образом сгущение будет перемещаться вдоль оси трубы все правее и правее. Распространяется сгущение, а не частицы воздуха. От одного конца трубы до другого. Каждая частица лишь колеблется влево-вправо около положения равновесия. Скорость распространения сгущенного состояния и будет скоростью распространения упругой деформации среды..

Если периодически повторять движение поршня вперед и назад, то в воздушной среде образуется ряд последовательных сгущений и разряжений, бегущих вдоль оси трубы. Такое движение называется волновым.

Расстояние от одного сгущенного состояния до следующего, т.е. расстояние между двумя последовательными точками среды, находящимися в одной фазе, называется длиной волны, а число волн, проходящих через точку в 1 с, - частотой колебательного движения .

Для звуковых волн частота звука является характеристикой звукового ощущения, известного под названием высоты звука или тона (до, ре, ми и т.д.). чем больше частота, тем выше тон.

Сила звука данного источника объективно определяется мощностью колебаний и пропорциональна квадрату их амплитуды.

Однако при субъективной оценке громкости звука играет роль и высота звука, так что звуки. Значительно отличающиеся по высоте, дают разные ощущения громкости.

П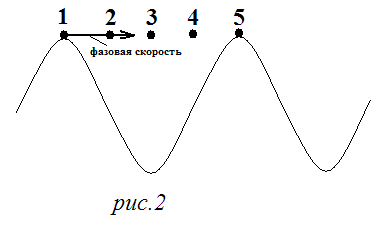о длине и частоте волны можно вычислить скорость звука:(9).

В теории волн различают понятия фазовой и групповой скорости. Первая равна скорости распространения фазы в пространстве (рис.2). Это – только математическое понятие.

Также как нельзя практически выделить строго монохроматический луч света с соответствующей ему строго определенной длиной волны, а всегда приходится иметь дело с пучком, представляющим собой смесь близко расположенных длин волн, так нельзя и получить звуковой волны строго определенной частоты. Кроме того, для передачи сигнала волна должна быть модулирована: необходимо, чтобы были разрывы и изменения амплитуды. При распространении звука такая модуляция происходит всегда: всякий источник звука посылает не одну волну строго определенной частоты, а несколько, хоть немного отличающихся друг от друга, волн. Как известно, при \том происходит интерференция, приводящая к биениям: волна разбивается на отдельные участки – пакеты. Энергия концентрируется в местах наибольших амплитуд и может восприниматься ухом или другим приемником как определенный сигнал. При этом в некоторых случаях максимум перемещается по пакету со скоростью, отличной от фазовой (рис.3).

Скорость сигнала или скорость звука есть скорость распространения подобных групп волн и поэтому называется групповой скоростью. С этой скоростью распространяется и энергия звука.

Для звуковых волн в воздухе и в воде групповая и фазовая скорости одинаковы. Это вызвано тем, что скорость звука, являясь скоростью распространения упругих деформаций среды, не зависит от частоты. Звуки любого типа распространяются одинаково. Разница лишь в громкости. Т.е. для звуковых волн не наблюдается дисперсия. Поэтому не оговаривают о фазовой или групповой скорости идет речь, а говорят просто о скорости звука.