
Определенный интеграл
.pdf
§10. Геометрическая интерпретация определенного интеграла
Краткие теоретические сведения В §1 мы рассмотрели задачу о вычислении площади криволинейной тра-
пеции, то есть фигуры, ограниченной осью Ох, кривой y=f(x), прямыми х=а,
х=b (f(x) – неотрицательная и непре-
рывная функция на [a, b]) (рис. 1).
Площадь криволинейной трапе-
ции численно равна интегралу от дан-
ной функции f(x) по данному отрезку
b
[a, b]: S f (x)dx. В этом и состоит
a
геометрическая интерпретация инте-
b
грала f (x)dx.
a
В частности, криволинейная трапеция может принимать следующий вид
(рис. 2, 3, 4):
Аналогично, фигуру, ограниченную осью Оу, прямыми y=c, y=d и кривой х=φ(у) (φ(у) – неотрицательная и непрерывная на [c, d] функция), также назы-
вается криволинейной трапецией (относительно оси Оу) (рис. 5):
31

d
Площадь этой трапеции S равна: S (y)dy .
c
Если криволинейная трапеция ограничена f(x), где f(x) – неположитель-
ная и непрерывная на [a, b] функция, то площадь S такой трапеции равна:
b
S f (x)dx (рис. 6):
a
Рассмотрим плоскую фигуру, ограниченную прямыми х=а, х=b и кривы-
ми у=f1(x) и у=f2(x) (f1(x)≤f2(x)). Функции f1(x) и f2(x) непрерывны на [a, b].
b
Площадь такой фигуры: S ( f2 (x) f1(x))dx (рис. 7):
a
32

Та же формула справедлива и для фигуры ограниченной пря-
мыми y=c, y=d и кривыми х=φ1(у)
и х=φ2(у), где φ1(у)≤φ2(у), φ1 и φ2
– непрерывны на [c, d] (рис. 8):
Пример 1. Вычислить пло-
щадь фигуры, ограниченной кри-
вой y 1 x2 , осью Ох и прямыми
4
х=1, х=4 (рис. 9):
4 |
1 |
|
2 |
|
1 |
|
x3 |
|
4 |
|
1 |
|
3 |
3 |
|
|
|
|
|
|
|
||||||||||
S |
|
x |
|
dx |
|
|
|
|
|
|
|
|
(4 |
|
1 ) |
4 |
|
4 |
3 |
|
|
12 |
|
||||||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
21 5,25 (ед.2).
4
Пример 2. Вычислить пло-
щадь фигуры, ограниченной кривой y 0, y sin x , x [0,2 ] (рис. 10):
В данном случае
2
S sin xdx sin xdx cosx 0
cosx 2 (cos cos0) cos2
cos ( 1 1) 1 ( 1) 4(ед.2 ).
Пример 3. Вычислить площадь фигуры, ограничен-
ной линиями y x2 , |
y |
1 |
x2 , |
|
|||
|
2 |
|
|
y 3x. |
|
|
|
33
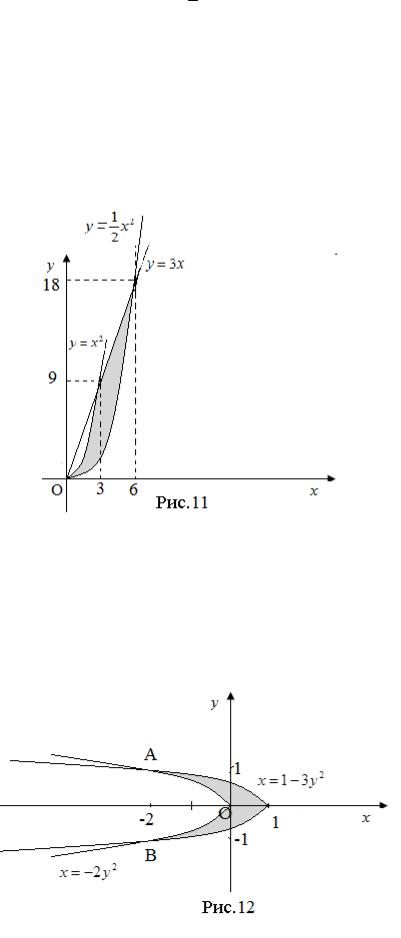
Здесь y x2 и y 1 x2 – параболы с вершиной в начале координат, осью
2
Оу и расположенные в верхней полуплоскости относительно оси Ох. Линия y 3x – прямая, проходящая через О(0, 0).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
Найдем точки пересечения линий: |
y x2 , |
и |
y |
|
|
|
x2, |
откуда получаем |
||||||||||||||||||||||||||||||||||||||
|
2 |
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
y 3x |
|
|
|
|
y 3x, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
точки О(0, 0), А(3, 9) и В(6, 18) (рис. 11): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Заштрихованная |
фигура |
||||||||||||||||||||||||||||||||||
|
|
|
|
|
имеет площадь |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
S (x2 |
х2 )dx (3х |
х2 )dx |
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
1 x3 |
|
3 |
|
|
3x |
2 |
|
6 |
|
1 x3 |
|
3 |
1 |
|
|
3 |
|
|
3 |
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3 |
|
0 |
|
) |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
2 |
3 |
|
|
0 |
|
|
|
2 |
|
|
|
3 |
2 |
|
|
3 |
|
0 |
6 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
3 |
(62 32 ) |
1 |
(63 33) |
9 |
|
81 |
|
63 |
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
2 |
|
|
|
2 |
2 |
|
|
||||||||||||
|
|
|
|
|
|
27 |
13,5(ед.2 ). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
4. |
|
|
|
Вычислить |
||||||||||||||||||||||||||||||
площадь фигуры, ограниченной линиями х 2у2 , |
х 1 3у2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
Здесь φ1(у)= 2у2 , φ2(у)=1 3у2 . Найдем точки пересечения данных пара- |
||||||||||||||||||||||||||||||||||||||||||||||
бол: |
х 2у2 , |
откуда А(-2,1), В(-2,-1) |
– искомые точки. Парабола |
х 2у |
2 |
||||||||||||||||||||||||||||||||||||||||||
|
у |
2 |
|
||||||||||||||||||||||||||||||||||||||||||||
|
х 1 3 |
|
, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
имеет вершину О(0,0), а |
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
парабола |
х 1 3у2 |
|
– |
вер- |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
шину (1,0) (рис. 12): |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Площадь |
|
|
S |
фигуры |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
равна: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||

|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
S ((1 3у2 ) ( 2у2 ))dу , |
|
так |
|
как |
на |
|
[-1, |
1] |
1 3у2 2y2 , |
||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
y3 |
|
1 |
1 |
|
1 |
3 |
3 |
|
|
4 |
|
2 |
). |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
S |
( у |
1)dу |
|
y |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
(1 ( 1) |
|
) (1 ( 1)) |
|
(ед. |
|
|
|
||||||
|
3 |
1 |
3 |
|
3 |
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 5. Вычислить площадь фигуры, ограниченной линиями y x 2,
y 4 x2 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
|
f1(x) x 2 |
|
и |
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
f2 (x) 4 x2 . Построим эти линии, |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
определив предварительно точки |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
их |
|
|
|
|
|
|
|
пересечения: |
y x 2, |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
, |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y 4 x |
|
||
|
|
|
|
|
|
|
|
|
|
|
x2 х 6 0, |
х1=2, х2=-3, а у1=0, |
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
у2=-5, отсюда А(2,0), В(-3,-60 – |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
искомые |
|
|
|
точки. |
Парабола |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
y 4 x2 |
имеет |
вершину (0,4) |
|
и |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
пересекает ось абсцисс в точке |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
х=-2 (рис. 13): |
|
|
|
|
|
|
|
|
|||||||||||||||||
Тогда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
2 |
|
|
|
2 |
|
x |
3 |
|
|
|
2 |
|
x |
2 |
|
|
|
2 |
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
S (4 x2 (х 2))dx ( х2 |
х 6)dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
6х |
|
3 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
3 |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
1 |
(23 |
( 3)3 ) |
1 |
(22 |
( 3)2 ) 6(2 ( 3)) |
1 |
35 |
5 |
30 |
125 |
20 |
5 |
(ед.2 ). |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
3 |
|
2 |
|
|
|
|
|
3 |
|
|
|
|
2 |
|
|
|
|
6 |
6 |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 6. Вычислить пло- |
||||||||||||||||||||
|
|
|
|
|
|
|
щадь |
|
|
|
|
|
|
фигуры, |
|
ограниченной |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x 1, 1 x 0, |
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
y f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
и осью абс- |
|||||||||||
|
|
|
|
|
|
|
|
(x) |
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
cosx,0 x |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
цисс (рис. 14): |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Здесь |
f(x) |
непрерывна |
на |
|||||||||||||||||
|
|
|
|
|
|
|
35 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

[ 1, ]; 2
0
S (x 1)dx
1
1 1 1 3 2 2
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
x |
2 |
|
|
|
01 |
|
|
|
1 |
|
|
|
|
||
|
|
|
|
|
|
|
|||||||||||
cosxdx |
|
|
|
х |
|
sin x |
|
|
|
(02 |
( 1)2 ) (0 ( 1)) (sin |
sin0) |
|||||
|
|
|
|
02 |
|||||||||||||
|
|
|
|
||||||||||||||
0 |
2 |
|
|
1 |
|
|
|
2 |
|
2 |
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(ед.2 ).
36

§11. Площадь криволинейного сектора
Краткие теоретические сведения Кривая может быть задана не прямоугольной системе координат, а в по-
лярной.
Криволинейным сектором называют фигуру, ограниченную дугой АВ кривой ρ=f(φ) и радиус-векторами ОА и ОВ, для которых φ=α, φ=β, (α<β) соот-
ветственно (рис. 15):
Площадь криволиней-
ного сектора вычисляется по
формуле: S 1 f ( ) 2 d .
2
Если ρ=f(φ) – непре-
рывная функция, которая принимает при φ=2π то же значение, что и при φ=0, то
кривая будет замкнутой. В этом случае S 1 f ( ) 2 d будет определять вели-
2
чину площади фигуры, ограниченной замкнутой линией.
Пример 1. Вычислить площадь фигуры, ограниченной линиями 3sin ,

 3cos .
3cos .
Здесь 3sin – полярное уравнение окружности
х2 у2 3у , которая имеет центр
|
0, |
3 |
и радиус |
3 |
, а |
|
|
||
3cos |
|||||||||
|
|
|
|
||||||
|
2 |
||||||||
|
|
2 |
|
|
|
|
|||
задает окружность с центром
|
3 |
|
|
и радиусом |
3 |
(рис. 16): |
|
|
,0 |
|
|
||
|
|
|||||
|
2 |
|
|
|
2 |
|
|
|
|
|
|
37

Из системы |
3sin , |
имеем tg |
1 |
|
, следовательно |
|
для точки Р |
|||
|
|
|
|
|
|
|
||||
3cos |
|
|
|
6 |
||||||
|
|
|
3 |
|
|
|
||||
пересечения окружностей.
Луч ОР разбивает фигуру на два криволинейных сектора, поэтому
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
S 9 |
|
6 |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
6 |
1 cos2 d 3 |
|
2 |
1 cos2 d |
9 |
|
9sin 2 |
3 |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
sin2 d 3 |
|
cos2 d 9 |
|
|
|
6 |
6 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
||||||
|
2 0 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
2 0 |
|
|
2 |
|
|
|
|
|
|
2 |
2 |
|
|
|
4 |
0 |
4 |
|
0 |
|
4 |
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
3 |
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
3 5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
sin2 |
|
|
|
|
( |
|
|
|
|
|
) |
|
( |
|
|
|
|
|
|
|
|
|
) |
|
( |
|
|
|
|
|
|
)(ед. |
|
). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
8 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
2 12 8 |
|
|
2 4 12 8 |
|
|
|
2 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 2. Вычислить площадь фигуры, ограниченной линией
1 cos .
Здесь линия 1 cos являет-
ся кардиоидой (рис. 17).
Фигура, ограниченная кардио-
идой симметрична относительно оси,
поэтому
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
S 2 |
|
(1 cos )2 d d 2 cos d cos2 d |
|
|
2sin 2 |
|
|
|
|
|||||||||||
|
|
|
||||||||||||||||||
|
|
|
|
|||||||||||||||||
2 |
|
|
|
2 |
|
0 |
||||||||||||||
0 |
|
|
|
|
0 |
0 |
0 |
|
0 |
|
|
|
|
|||||||
|
1 |
|
|
|
|
|
3 |
|
|
|
|
|
|
|
||||||
|
sin2 |
|
|
(ед.2 ). |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
4 |
|
|
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
38
§12. Площадь криволинейной трапеции, ограниченной линией, заданной параметрически
Краткие теоретические сведения Пусть криволинейная трапеция ограничена кривой, заданной параметри-
чески: x (t), |
пусть t1 и t2 значения параметра t, отвечающие значениям x=a, |
||
y (t), |
|
|
|
x=b соответственно: a=φ(t1), b=ψ(t2). |
|
||
|
b |
|
|
В формуле S уdx |
проведем замену переменной: x (t), |
dx '(t)dt. То- |
|
|
a |
|
|
t2 |
|
|
|
гда S (t) '(t)dt . |
|
|
|
t1 |
|
|
|
|
|
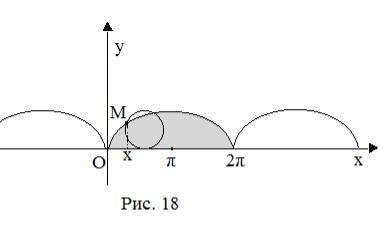
Пример 1. Найти пло- |
|
|
|
щадь фигуры, ограниченной |
|
|
|
осью абсцисс и одной аркой |
|
|
|
циклоиды: |
x t sint, |
|
|
|
|
|
|
|
y 1 cost, |
|
|
t 0,2 (рис. 18). |
|
|
|
Циклоида описывается |
|
|
|
произвольной |
точкой М |
окружности круга с радиусом r=1, которая катится без трения и скольжения по прямой Ох.
Здесь (t) t sint, (t) 1 cost , t1=0, t2=2π, '(t) 1 cost , поэтому
2 |
2 |
2 |
2 |
|
|
2 |
||||
|
02 |
1 |
|
1 |
|
|||||
S |
(1 cost)2 dt (1 2cost cos2 tdt t |
2sint |
t |
|
sin 2t |
3 (ед.2 ). |
||||
|
4 |
|||||||||
0 |
0 |
2 |
|
0 |
|
0 |
||||
0 |
|
|
|
|
|
|||||
Замечание. Циклоида – линия, которая имеет применения в прикладной
технике, теории механизмов.
Пример |
2. Найти площадь фигуры, ограниченной линией: |
x 12cost 5sint, |
t 0,2 . |
|
|
y 5cost 12sint, |
|
|
39 |
|
|
Здесь |
|
|
|
|
(t) 12cost 5sint, |
|
|
|
(t) 5cost 12sint, |
|||||||||||||||
'(t) 12sint 5cost 5cost |
12sint , |
|
|
|
|
|
|
|
|
поэтому |
||||||||||||||||
2 |
|
|
|
|
|
|
2 |
1 cos2t |
|
|
|
|
|
2 |
|
2 |
1 cos2t |
|
||||||||
S (5cost 12sint)2 dt 25 |
dt 60 |
sin2tdt |
144 |
dt |
||||||||||||||||||||||
|
|
2 |
||||||||||||||||||||||||
0 |
|
|
|
|
|
|
|
0 |
|
|
|
2 |
|
|
|
|
|
0 |
|
|
0 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
25( |
1 |
t |
|
2 |
|
1 |
sin 2t |
|
2 ) 30cos2t |
|
2 |
144( |
1 |
t |
|
2 |
|
1 |
sin2t |
|
2 ) 25 144 169 (ед.2 ). |
|||||
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
2 |
|
|
0 |
4 |
|
|
0 |
|
|
0 |
2 |
|
|
0 |
4 |
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Задачи для практического занятия Вычислить площади следующих фигур:
1. Фигура ограничена линиями y |
x2 |
,y 0,x 2; |
|
||
2 |
|
|
2.Фигура ограничена линиями y x2,x 1 0,x 2;
3.Фигура ограничена линиями y x2,x y2 ;
4.Фигура ограничена линиями x 2y2,x 2;
5.Фигура ограничена линиями y x2 2x 3,y 3x 1;
6.Фигура ограничена линиями y 8x 2x2,x 5;
7. Фигура ограничена линиями y |
1 |
,y x2 ,y 0,x 3; |
|
x |
|||
|
|
8.Фигура ограничена линиями y ex ,y 0,x 4,x 0;
9.Фигура ограничена линиями y 3 x2 ,y 1;
10.Фигура ограничена линиями y ln x,y 0,x 2,x 4;
11.Фигура ограничена осью Ох, y 1 x2 ,x 2;
12.Фигура ограничена параболой y x2 2x 3, осью Ох;
13.Фигура ограничена осью Оу и линией y2 2x 9;
14.Фигура ограничена осью абсцисс и кривыми y (x 1)2 ,y (x 1)2 ;
15.Фигура ограничена осями координат и линией y x2 4х 3;
16.Фигура ограничена линиями x2 9у 0,x 3у 6 0;
17.Фигура ограничена y 2х х2,y x 0;
18.Фигура ограничена y2 2х,y х2 х;
40
